---

第一章 基础算法（二）

---

高精度

---

高精度问题其实只有使用 C++ 编程语言的同学需要关注，使用 java 或 python 编程语言的同学不需要太多关注。因为 java 有大整数类，python 自带的数据范围默认就是无限大，而 C++ 没有相对应的处理大整数运算的数据结构。

高精度的考察主要分为四种： 高 精 度 { 加 法 A + B 减 法 A − B 乘 法 A × a 除 法 A ÷ a 高精度

高精度⎩⎪⎪⎪⎨⎪⎪⎪⎧​加法A+B减法A−B乘法A×a除法A÷a​，其中 $A,B$ 的位数 $⩽10^6$，$a⩽10000$。

两个大整数相乘/相除应用的场景不多，并且 $A÷B$ 即两个大整数相除处理起来非常复杂，所以这里不作考虑。

如何存储大整数？

因为 C++ 中没有能够存储大整数的数据类型的，所以可以将大整数的每一位存在数组当中。

例如有一个大整数 $A=123456789$，那么存储到数组当中时，会出现一个问题：**低位在前还是高位在前呢？**即假设有一个数组 $s$，则应该让 $s[0]=1$ 还是让 $s[0]=9$？

应该是低位在前，即 $s[0]=9,s[1]=8\cdots s[8]=1$，这样存储会比较好。因为两个整数相加可能会存在进位，这样进位时会在高位的地方补上数字，而将高位存储到数组的末尾，可以更方便地新增数字。

即用 $s[0]$ 存储整数的个位，用 $s[1]$ 存储整数的十位，以此类推。

高精度加法

高精度加法是模拟人工加法的过程。
1 2 3 + 8 9 2 1 2

+​12​281​392​​
所以对于两个大整数 $A,B$，加法运算就是模拟人工加法的过程，在从低位到高位相加时，考虑进位即可。
A 3 A 2 A 1 A 0 + B 2 B 1 B 0 C 3 C 2 C 1 C 0

+A3C3A2B2C2A1B1C1A0B0C0$$\begin{array}{ccccc}& A_3& A_2& A_1& A_0\\ +& & B_2& B_1& B_0\\ & C_3& C_2& C_1& C_0\end{array}$$

+​A3​C3​​A2​B2​C2​​A1​B1​C1​​A0​B0​C0​​​

即 $C_0=(A_0+B_0)\%10$；

若 $A_0+B_0⩾10$，则说明需要进位，故 $C_1=(A_0+B_0)/10+(A_1+B_1)\%10$；

一般地，有 $C_i=(A_{i-1}+B_{i-1})/10+(A_i+B_i)\%10$；

如果 $A_i$ 或 $B_i$ 有其中一个不存在，则用 $0$ 代替即可。

依次类推进行下去，就可以实现模拟人工加法。

AcWing 791. 高精度加法

原题链接

给定两个正整数（不含前导 $0$），计算它们的和。

输入格式

共两行，每行包含一个整数。

输出格式

共一行，包含所求的和。

数据范围

$1\le$ 整数长度 $\le 10^5$

输入样例：

12
23
1
2

输出样例：

35
1

时/空限制： 1s / 64MB
来源： 模板题
算法标签：高精度

yxc’s Solution

• 在 C++ 编程语言中，可以使用vector来代替数组来存储大整数，因为vector自带size函数，可以表示数组的长度，就不需要开额外的变量，存储数组的长度这一信息了。

#include <iostream>
#include <vector>

using namespace std;

const int N = 1e6 + 10;


vector<int> add(vector<int> &A, vector<int> &B)
//这里使用引用&，是为了增加效率，如果不加引用，在调用函数时会将 A 和 B 都复制一遍，会增加耗时
{
	vector<int> C;

	int tmp = 0;
	for (int i=0; i < A.size() || i < B.size(); i ++ )
	{
		if (i < A.size()) tmp += A[i];
		if (i < B.size()) tmp += B[i];
		C.push_back(tmp % 10);
		tmp /= 10;
	}
	if (tmp) C.push_back(tmp);
	return C;
}

int main()
{
	string a, b;
	vector<int> A, B;

	cin >> a >> b; // a = "123456"
	for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0'); // A = [6, 5, 4, 3, 2, 1]
	for (int i = b.size() - 1; i >= 0; i -- ) B.push_back(b[i] - '0');

	vector<int> C = add(A, B);

	for (int i = C.size() - 1; i >= 0; i -- ) cout << C[i];

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

---

高精度减法

加减乘除的高精度运算中，大整数的存储方式都是一样的。这样更方便在需要多种运算的题目中统一变量的数据类型。

高精度减法也是模拟人工减法的过程。
1 2 3 − 8 9 3 4

−​1​283​394​​
对于两个大整数 $A,B$，其减法过程也是模拟人工减法的过程，从低位到高位进行相减和借位。
A 3 A 2 A 1 A 0 − B 2 B 1 B 0 C 3 C 2 C 1 C 0

$$\begin{array}{}\end{array}$$

−A3C3A2B2C2A1B1C1A0B0C0$$\begin{array}{ccccc}& A_3& A_2& A_1& A_0\\ -& & B_2& B_1& B_0\\ & C_3& C_2& C_1& C_0\end{array}$$

−​A3​C3​​A2​B2​C2​​A1​B1​C1​​A0​B0​C0​​​

即 $C_0=A_0-B_0$；

若不够减（如 $A_i<B_i$）就需要借位，即 A i − B i { ⩾ 0 , A i − B i < 0 , A i − B i + 10 A_i-B_i

{⩾0,<0,Ai−BiAi−Bi+10$$\{\begin{array}{ll}⩾0,& A_i-B_i\\ <0,& A_i-B_i+10\end{array}$$

Ai​−Bi​{⩾0,<0,​Ai​−Bi​Ai​−Bi​+10​，但若需要借位，则 $A_{i+1}$ 就会减去 $1$；

需要注意的是，高精度减法的模板是默认 $A⩾B$ 的，这样可以避免运算结果是负数，如果 $A<B$，则将它们交换就可以使用高精度减法的模板了。

因为 $A-B=-(B-A)$，故如果 $A-B$ 是负数，则 $B-A$ 就应该是正数。
A − B { A ⩾ B → A − B A < B → − ( B − A ) A-B

{A⩾BA<B→→A−B−(B−A)$$\{\begin{array}{lll}A⩾B& \to & A-B\\ A<B& \to & -(B-A)\end{array}$$

A−B{A⩾BA<B​→→​A−B−(B−A)​

AcWing 792. 高精度减法

原题链接

给定两个正整数（不含前导 $0$），计算它们的差，计算结果可能为负数。

输入格式

共两行，每行包含一个整数。

输出格式

共一行，包含所求的差。

数据范围

$1\le$ 整数长度 $\le 10^5$

输入样例：

32
11
1
2

输出样例：

21
1

时/空限制： 1s / 64MB
来源： 模板题
算法标签：高精度

yxc’s Solution

• 在使用高精度减法的模板之前，需先判断 $A$ 与 $B$ 的大小关系。

#include <iostream>
#include <vector>

using namespace std;

const int N = 1e6 + 10;

//判断是否有 A>=B
bool cmp(vector<int> &A, vector<int> &B)
{
	if (A.size() != B.size()) return A.size() > B.size();
	//如果位数不同，则位数多的数字更大

	for (int i = A.size(); i >= 0; i -- )
		if (A[i] != B[i])
			return A[i] > B[i];
	//如果位数相同，高位大的数字更大

	//因为判断是否 A>=B，故 A=B 也要返回 true
	return true;
}

vector<int> sub(vector<int> &A, vector<int> &B)
{
	vector<int> C;
	int tmp = 0;
	for (int i = 0 ; i < A.size(); i ++ )
	{
		tmp = A[i] - tmp;
		if (i < B.size()) tmp -= B[i];
		C.push_back((tmp + 10) % 10);
		/*
			这里是将借位和不借位两种情况合二为一的写法
			如果不借位，则 tmp>0，是否 +10 对 (tmp + 10) % 10 的结果没有影响
			如果借位，则 (tmp + 10) % 10 应该才是当前位的数字
		*/
		if (tmp < 0) tmp = 1;
		else tmp = 0;
	}

	while(C.size() > 1  && C.back() == 0) C.pop_back();
	//去除前导零

	return C;
}

int main()
{
	string a, b;
	vector<int> A, B;

	cin >> a >> b; 
	for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0'); 
	for (int i = b.size() - 1; i >= 0; i -- ) B.push_back(b[i] - '0');

	
	if (cmp(A,B))
	{
		vector<int> C = sub(A, B);
		for (int i = C.size() - 1; i >= 0; i -- ) cout << C[i];
	}
	else
	{
		vector<int> C = sub(B, A);
		cout<<"-";
		for (int i = C.size() - 1; i >= 0; i -- ) cout << C[i];
	}
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

---

高精度乘法

高精度乘法也是模拟人工乘法的过程，但由于 $A\times a$ 中，$a$ 较小，所以过程会有所不同。
A 5 A 4 A 3 A 2 A 1 × a

×​A5​​A4​​A3​​A2​​A1​a​​
即个位为 $C_0=A_0\times a\%10$，并且向十位进位 $\lfloor \frac{A_0\times a}{10}\rfloor$。

而十位为 $C_1=(A_1\times a+\lfloor \frac{A_0\times a}{10}\rfloor )\%10$，再向百位进位，并以此类推。

举例，如
1 2 3 × 12

×12312$$\underline{\begin{array}{cccc}& 1& 2& 3\\ \times & & & 12\end{array}}$$

×​1​2​312​​
个位为 $C_0=(3\times 12)\%10=36\%10=6$，此时进位 $t_1=\lfloor \frac{36}{10}\rfloor =3$；

十位为 $C_1=(2\times 12+t_1)\%10=(24+3)\%10=27\%10=7$，此时进位 $t_2=\lfloor \frac{27}{10}\rfloor =2$；

百位为 $C_2=(1\times 12+t_2)\%10=(12+2)\%10=14\%10=4$，此时进位 $t_3=\lfloor \frac{14}{10}\rfloor =1$；

千位即为 $C_3=(0\times 12+t_3)\%10=1\%10=1$，此时没有进位，且已经计算完毕；

故 $123\times 12=1476$。

故这里乘法与加减法的不同在于，会将 $a$ 看作一个整体进行运算。

AcWing 793. 高精度乘法

原题链接

给定两个非负整数（不含前导 $0$） $A$ 和 $B$，请你计算 $A\times B$ 的值。

输入格式

共两行，第一行包含整数 $A$，第二行包含整数 $B$。

输出格式

共一行，包含 $A\times B$ 的值。

数据范围

$1\le A$ 的长度 $\le 100000$,
$0\le B\le 10000$

输入样例：

2
3
1
2

输出样例：

6
1

时/空限制： 1s / 64MB
来源： 模板题
算法标签：高精度

yxc’s Solution

#include <iostream>
#include <vector>

using namespace std;

vector<int> mul(vector<int> &A, int b)
{
	vector<int> C;

	int tmp = 0;
	for(int i = 0; i < A.size() || tmp; i ++ )
	{
		if (i < A.size()) tmp += A[i] * b;
		C.push_back(tmp % 10);
		tmp /= 10;
	}
	while (C.size() > 1 && C.back() == 0) C.pop_back();
	
	return C;
}

int main()
{
	string a;
	int b;

	cin >> a >> b;

	vector<int> A;
	for (int i = a.size()-1; i >= 0; i -- ) A.push_back(a[i]-'0');

	vector<int> C = mul(A, b);

	for (int i = C.size() - 1; i >= 0 ; i -- ) cout << C[i];

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

---

高精度除法

先来看一下模拟人工除法的过程。
11 0 1 1 2 ∣ 1 2 3 4 0 1 2 1 1 1 3 1 1 2 4 2 2 2

11​∣​01011​122111​133122​24422​​
抽象出来，即对于每次剩下的余数 $r$，都来计算 $\lfloor \frac{a}{r}\rfloor$ 的值是多少，放到商的对应位置上去。
$$\begin{gathered} C_3{C}_2{C}_1{C}_0 \\ a\overline{|A_3{A}_2{A}_1{A}_0} \end{gathered}$$

即 $C_3=\lfloor \frac{A_3}{b}\rfloor ,r_1=A_3\%b$；

即 $C_2=\lfloor \frac{A_2+r_1}{b}\rfloor ,r_2=(A_2+r_1\times 10)\%b$；

以此类推。

可以发现，除法是从最高位开始算的，和前面的加减乘有很大的不同。

AcWing 794. 高精度除法

原题链接

给定两个非负整数（不含前导 $0$） $A$，$B$，请你计算 $A/B$ 的商和余数。

输入格式

共两行，第一行包含整数 $A$，第二行包含整数 $B$。

输出格式

共两行，第一行输出所求的商，第二行输出所求余数。

数据范围

$1\le A$ 的长度 $\le 100000$,
$1\le B\le 10000$,
$B$ 一定不为 $0$

输入样例：

7
2
1
2

输出样例：

3
1
1
2

时/空限制： 1s / 64MB
来源： 模板题
算法标签：高精度

yxc’s Solution

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

// A / b，商是 C，余数是 r
vector<int> div(vector<int> &A, int b, int &r)
//余数是通过引用 &  返回其值的
{
	vector<int> C;
	
	r = 0;
	for(int i = A.size() - 1; i >= 0; i -- )
	{
		r = r * 10 + A[i];
		C.push_back(r / b);
		r %= b;
	}
	reverse(C.begin(),C.end());
	//因为这里的 C 实际上是从高位开始存的，所以需要翻转过来
	while (C.size() > 1 && C.back() == 0) C.pop_back();
	
	return C;
}

int main()
{
	string a;
	int b;

	cin >> a >> b;

	vector<int> A;
	for (int i = a.size()-1; i >= 0; i -- ) A.push_back(a[i]-'0');

	int r;
	vector<int> C = div(A, b, r);

	for (int i = C.size() - 1; i >= 0 ; i -- ) cout << C[i];
	cout << '\n' << r;

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

---

前缀和

---

若有一个数组为 $a_1,a_2,a_3,\cdots ,a_n$，则其前缀和数组可以定义为 $S_i=a_1+a_2+\cdots +a_i=\sum _{x=1}^i{a}_x$。

这里要注意一点，即原数组与前缀和数组的下标一般从 $1$ 开始。

如何求前缀和？

for (int i = 1; i <= n; i ++ )
    S[i] = S[i -1] + a[i];
1
2

即 $S_i$ 是通过 $S_{i-1}$ 算出来的，因为 $S_{i-1}=a_1+a_2+\cdots +a_{i-1}=\sum _{x=1}^{i-1}{a}_x$，故再加上一个 $a_i$ 恰好就等于 $S_i$。

这里需要定义一个边界值，为 $S_0=0$。

前缀和数组的求解的时间复杂度为 $O(n)$。

前缀和的作用

前缀和数组可以快速地算出原数组中某一段 $[L,R]$ 的区间和。

如果不用前缀和数组，则求出原数组中某一段的区间和的时间复杂度为 $O(n)$。

int sum = 0;
for (int i = L; i <= R; i ++ )
    sum += a[i];
1
2
3

如果使用前缀和数组，则这一段区间和即为 $S_R-S_{L-1}$。

因为 $S_R=a_1+a_2+\cdots +a_R=\sum _{x=1}^R{a}_x$，$S_{L-1}=a_1+a_2+\cdots +a_{L-1}=\sum _{x=1}^{L-1}{a}_x$，两者相减恰好等于 $S_R-S_{L-1}=a_L+a_{L+1}+\cdots +a_R=\sum _{x=L}^R{a}_x$。

所以，如果有前缀和数组，就可以在 $O(1)$ 的时间复杂度内求解区间和。

因此，前缀和数组下标一般从 $1$ 开始，这样 $S_0$ 就可以直接赋值为 $0$，而不需要考虑多余的边界情况。

例如要求的区间为 $[1,x]$，这样答案应该为 $S_x-S_0$，因为 $S_0=0$ 就不要进行多余的处理，直接使用 $S_x-S_0=S_x$ 这一结果即可。

前缀和并不是这一简单的结论，而是一种思想，除了这一作用还有更广泛的应用。

AcWing 795. 前缀和

原题链接

输入一个长度为 $n$ 的整数序列。

接下来再输入 $m$ 个询问，每个询问输入一对 $l,r$。

对于每个询问，输出原序列中从第 $l$ 个数到第 $r$ 个数的和。

输入格式

第一行包含两个整数 $n$ 和 $m$。

第二行包含 $n$ 个整数，表示整数数列。

接下来 $m$ 行，每行包含两个整数 $l$ 和 $r$，表示一个询问的区间范围。

输出格式

共 $m$ 行，每行输出一个询问的结果。

数据范围

$1\le l\le r\le n$,
$1\le n,m\le 100000$,
$-1000\le$ 数列中元素的值 $\le 1000$

输入样例：

5 3
2 1 3 6 4
1 2
1 3
2 4
1
2
3
4
5

输出样例：

3
6
10
1
2
3

时/空限制： 2s / 64MB
来源： 模板题
算法标签：前缀和

yxc’s Solution

#include<iostream>

using namespace std;

const int N = 100010;

int n, m;
int a[N], s[N];

int main()
{
	scanf("%d %d", &n, &m);
	for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);

	for (int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + a[i]; // 前缀和的初始化

	while (m -- )
	{
 		int l, r;
 		scanf("%d %d", &l, &r);
 		printf("%d\n", s[r] - s[l - 1]); // 区间和的计算
	}

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

---

二维前缀和

对于一个大小为 $n\times m$ 的矩阵 $a$，其二维前缀和为 $S_{ij}=\sum _{x=1}^i\sum _{y=1}^j{a}_{xy}$，即它为矩阵左上角所有元素的和。

二维前缀和

如下图所示，如果想要求解左上角为 $(x_1,y_1)$，右下角为 $(x_2,y_2)$ 的子矩阵的所有元素和，其答案应为 $S_{x_2{y}_2}-S_{x_1-1,y_2}-S_{x_2,y_1-1}+S_{x_1-1,y_1-1}$。

子矩阵的和

即左上角所有元素的和 $S_{x_2{y}_2}$，减去左侧长方形矩阵的所有元素的和 $S_{x_2,y_1-1}$，再减去上侧长方形矩阵的所有元素的和 $S_{x_1-1,y_2}$；

此时以 $(1,1)$ 为左上角，$(x_1-1,y_1-1)$ 为右下角的矩阵的元素被减去了两次，所以需要加回来一次，即加上 $S_{x_1-1,y_1-1}$。

如何求得 $S_{ij}$ ？

类似于子矩阵的和，有如下代码：

for (int i = 1; i <= n; i ++ )
    for (int j = 1; j <= m; j ++)
        S[i][j] = a[i][j] + S[i - 1][j] + S[i][j - 1] - S[i-1][j-1];
1
2
3

这其实是和子矩阵的和相反的思路，即当前 $(i,j)$ 这一位置的元素，加上左侧长方形矩阵的所有元素的和 $S_{i,j-1}$，再加上上侧长方形矩阵的所有元素的和 $S_{i-1,j}$；

此时以 $(1,1)$ 为左上角，$(i-1,j-1)$ 为右下角的矩阵的元素被加上了两次，所以需要减去一次，即减去 $S_{i-1,j-1}$。

二维前缀和中包含了一些容斥原理的思想，会增加一些难度。

对于边界，可以发现 $S_{00},S_{i,0},S_{0,j}(0⩽i⩽n,0⩽j⩽m)$ 均为 $0$。

AcWing 796. 子矩阵的和

原题链接

输入一个 $n$ 行 $m$ 列的整数矩阵，再输入 $q$ 个询问，每个询问包含四个整数 $x_1,y_1,x_2,y_2$，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式

第一行包含三个整数 $n$，$m$，$q$。

接下来 $n$ 行，每行包含 $m$ 个整数，表示整数矩阵。

接下来 $q$ 行，每行包含四个整数 $x_1,y_1,x_2,y_2$，表示一组询问。

输出格式

共 $q$ 行，每行输出一个询问的结果。

数据范围

$1\le n,m\le 1000$,
$1\le q\le 200000$,
$1\le x_1\le x_2\le n$,
$1\le y_1\le y_2\le m$,
$-1000\le$ 矩阵内元素的值 $\le 1000$

输入样例：

3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
1
2
3
4
5
6
7

输出样例：

17
27
21
1
2
3

时/空限制： 2s / 64MB
来源： 模板题
算法标签：前缀和

yxc’s Solution

#include <iostream>

using namespace std;

const int N = 1010;

int n, m, q;
int a[N][N], s[N][N];

int main()
{
	scanf("%d %d %d", &n, &m, &q);
	for (int i = 1; i <= n; i ++ )
		for (int j = 1; j <= m; j ++ )
			scanf("%d", &a[i][j]);

	for (int i = 1; i <= n; i ++ )
		for (int j = 1; j <= m; j ++ )
			s[i][j] = a[i][j] + s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];

	while (q -- )
	{
		int x1, y1, x2, y2;
		scanf("%d %d %d %d", &x1, &y1, &x2, &y2);
		printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
	}

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

---

差分

---

差分其实是前缀和的逆运算。

对于一个数组 $a_1,a_2,\cdots ,a_n$，要求构造一个数组 $b_1,b_2,\cdots ,b_n$，使得 $a_i=b_1+b_2+\cdots +b_i=\sum _{x=1}^i{b}_x$，即数组 $a$ 是数组 $b$ 的前缀和数组，此时数组 $b$ 称为数组 $a$ 的差分数组。

构造方法其实很简单，首先有 $b_1=a_1$；

其次有 $b_2=a_2-a_1,b_3=a_3-a_2,\cdots ,b_n=a_n-a_{n-1}$；

差分的作用

只要有差分数组，就可以通过求其前缀和在 $O(n)$ 的时间复杂度内求出原数组。

AcWing 797. 差分

原题链接

输入一个长度为 $n$ 的整数序列。

接下来输入 $m$ 个操作，每个操作包含三个整数 $l,r,c$，表示将序列中 $[l,r]$ 之间的每个数加上 $c$。

请你输出进行完所有操作后的序列。

输入格式

第一行包含两个整数 $n$ 和 $m$。

第二行包含 $n$ 个整数，表示整数序列。

接下来 $m$ 行，每行包含三个整数 $l$，$r$，$c$，表示一个操作。

输出格式

共一行，包含 $n$ 个整数，表示最终序列。

数据范围

$1\le n,m\le 100000$,
$1\le l\le r\le n$,
$-1000\le c\le 1000$,
$-1000\le$ 整数序列中元素的值 $\le 1000$

输入样例：

6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1
1
2
3
4
5

输出样例：

3 4 5 3 4 2
1

时/空限制： 1s / 64MB
来源： 模板题, Hulu面试题
算法标签：差分

yxc’s Solution

• 若原数组 $a$ 的某一区间 $[l,r]$ 全部加上 $c$，对于差分数组 $b$ 会有怎样的影响呢？
• 如果让 $b_l$ 加上 $c$，可以发现用差分数组 $b$ 还原数组 $a$ 时，$a_1\sim a_{l-1}$ 的值不会发生变化，而 $a_l\sim a_n$ 的值都会加上 $c$；
• 但是需要让 $a_{r+1}\sim a_n$ 不加上这个 $c$，所以需要打一个补丁，即 $b_{r+1}$ 需要减去 $c$。
• 差分数组其实也不需要刻意构造，可以假设原数组的元素都为 $0$，随后读入原数组的元素，即为在某一个单个区间 $[x,x]$ 进行加上该元素 $a_x$ 的操作。

#include <iostream>

using namespace std;

const int N = 100010;

int n, m;
int a[N], b[N];

void insert(int l, int r, int c)
{
	b[l] += c;
	b[r + 1] -= c;
}

int main()
{
	scanf("%d %d", &n, &m);
	for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);

	for (int i = 1; i <= n; i ++ ) insert(i,i,a[i]);

	while (m -- )
	{
		int l, r, c;
		scanf("%d %d %d", &l, &r, &c);
		insert(l, r, c);
	}

	for (int i = 1; i <= n; i ++ ) b[i] += b[i - 1];

	for (int i = 1; i <= n; i ++ ) printf("%d ", b[i]);
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

---

二维差分

同样地，对于大小为 $n\times m$ 的矩阵 $a$，可以构造其差分矩阵 $b$，使得 $a_{ij}=\sum _{x=1}^i\sum _{y=1}^j{b}_{ij}$。

如果想让左上角为 $(x_1,y_1)$，右下角为 $(x_2,y_2)$ 的子矩阵范围内的元素都加上 $c$，则应该先让 $b_{x_1{y}_1}$ 加上 $c$；

但此时左上角为 $(x_1,y_1)$，右下角为 $(n,m)$ 的子矩阵范围内的元素都会加上 $c$，就需要将下侧长方形矩阵内的所有元素减去 $c$，即 $b_{x_2+1,y1}$ 减去 $c$，再将右侧长方形矩阵内的所有元素减去 $c$，即 $b_{x_1,y_2+1}$ 减去 $c$；

此时左上角为 $(x_2+1,y_2+1)$，右下角为 $(n,m)$ 的子矩阵范围内的所有元素被减去了两次 $c$，需要加回来一次，即 $b_{x_2+1,y_2+1}$ 需要加上 $c$。

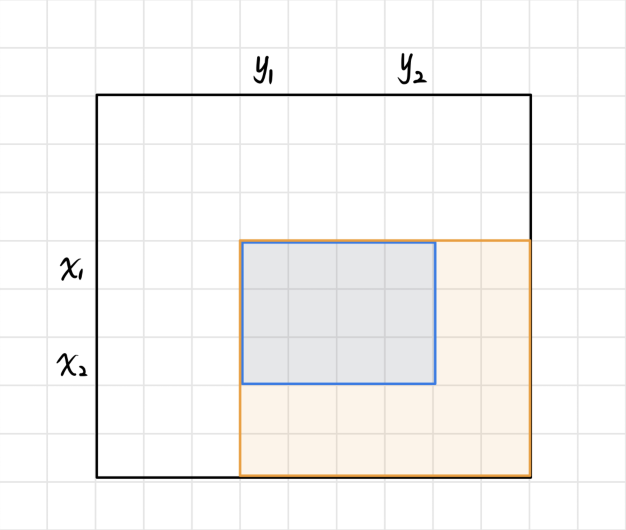
差分矩阵

同样地，可以通过进行单个元素的子矩阵的修改，由原矩阵 $a$ 构造出差分矩阵 $b$。

AcWing 798. 差分矩阵

原题链接

输入一个 $n$ 行 $m$ 列的整数矩阵，再输入 $q$ 个操作，每个操作包含五个整数 $x_1,y_1,x_2,y_2,c$，其中 $(x_1,y_1)$ 和 $(x_2,y_2)$ 表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上 $c$。

请你将进行完所有操作后的矩阵输出。

输入格式

第一行包含整数 $n,m,q$。

接下来 $n$ 行，每行包含 $m$ 个整数，表示整数矩阵。

接下来 $q$ 行，每行包含 $5$ 个整数 $x_1,y_1,x_2,y_2,c$，表示一个操作。

输出格式

共 $n$ 行，每行 $m$ 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围

$1\le n,m\le 1000$,
$1\le q\le 100000$,
$1\le x_1\le x_2\le n$,
$1\le y_1\le y_2\le m$,
$-1000\le c\le 1000$,
$-1000\le$ 矩阵内元素的值 $\le 1000$

输入样例：

3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
1
2
3
4
5
6
7

输出样例：

2 3 4 1
4 3 4 1
2 2 2 2
1
2
3

时/空限制： 2s / 64MB
来源： 模板题
算法标签：差分

yxc’s Solution

#include <iostream>

using namespace std;

const int N = 1010;

int n, m, q;
int a[N][N], b[N][N];

void insert(int x1, int y1, int x2, int y2, int c)
{
	b[x1][y1] += c;
	b[x2 + 1][y1] -= c;
	b[x1][y2 + 1] -= c;
	b[x2 + 1][y2 + 1] += c;
}

int main()
{
	scanf("%d %d %d", &n, &m, &q);

	for (int i = 1; i <= n; i ++ )
		for (int j = 1; j <= m; j ++ )
			scanf("%d", &a[i][j]);

	for (int i = 1; i <= n; i ++ )
		for (int j = 1; j <= m; j ++ )
			insert(i, j, i, j, a[i][j]);

	while (q -- )
	{
		int x1,y1,x2,y2,c;
		scanf("%d %d %d %d %d", &x1, &y1, &x2, &y2, &c);
		insert(x1,y1,x2,y2,c);
	}

	for (int i = 1; i <= n; i ++ )
		for (int j = 1; j <= m; j ++ )
			b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];

	for (int i = 1; i <= n; i ++ )
	{
		for (int j = 1; j <= m; j ++ )
			printf("%d ", b[i][j]);
		puts("");
	}

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

---

本文档基于 AcWing算法基础课 制作

视频链接：第一章 基础算法（二）- AcWing

文档版本：

var1.0 完成于2022.07.04.