---

一、什么是栈和队列？

栈是一种后进先出（Last in First out）的线性表，简称 LIFO，只允许在一端进行插入和删除操作；
队列是一种先进先出（FIrst in First out）的线性表，简称FIFO，只允许在一端进行插入操作，在另一端进行删除操作。

---

1.栈的实现原理

栈有栈的核心操作为栈顶入栈、栈顶出栈两个操作，如图：

有1 ，3 ，2 ，4 ，5分别进行入栈出栈操作

栈的应用及操作看这里

---

2.1单调栈

顾名思义，单调栈就是有单调性质的栈
现对1 ，3 ，2 ，4 ，5进行模拟操作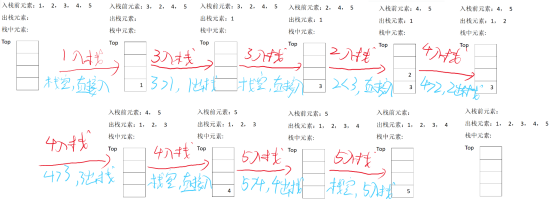

• 1入栈时，栈为空，直接入栈，栈中元素为：1
• 3入栈时，栈顶元素1比3小，1出栈，栈为空，3入栈，栈中元素为：3
• 2入栈时，栈顶元素3比2大，直接入栈，栈中元素为：3，2
• 4入栈时，栈顶元素2比4小，2出栈，栈顶元素3比4小，3出栈，栈为空，4入栈，栈中元素为：4
• 5入栈时，栈顶元素4比5小，4出栈，栈为空，5入栈，栈中元素为5

---

伪代码

for (遍历数组){
	if (栈空 || 栈顶元素 >= 当前元素){
		入栈;
	} else {
		while (栈不为空 && 栈顶元素 < 当前元素){
			栈顶元素出栈;
		}
		当前元素入栈;
	}
}
1
2
3
4
5
6
7
8
9
10

2.3应用实例

题目来源 ：acwing 830.单调栈

题目描述 :

给定一个长度为 N 的整数数列，输出每个数左边第一个比它小的数，如果不存在则输出 −1。

输入格式

第一行包含整数 N，表示数列长度。

第二行包含 N 个整数，表示整数数列。

输出格式

共一行，包含 N 个整数，其中第 i 个数表示第 i 个数的左边第一个比它小的数，如果不存在则输出 −1。

数据范围

1≤N≤105
1≤数列中元素≤109

输入样例

5
3 4 2 7 5
1
2

输出样例

-1 3 -1 2 2
1

模拟单调栈：

    #include <iostream>
    
    using namespace std;
    
    const int N=100010;
    
    int n;
    int skt[N],tt;
    
    int main()
    {
    	cin>>n;
    	while(n--)
    	{
    		int x;
    		cin>>x;
    		while(tt&&skt[tt]>=x)	tt--;
    		if(tt)	cout<<skt[tt]<<' ';
    		else	cout<<-1<<' ';
    		
    		skt[++tt]=x; 
    	}
    	return 0;
     } 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

3.1 队列

对1， 3， 2， 4， 5进行模拟操作如图

3.2 应用实例

题目来源 ：acwing 829.模拟队列

题目描述 :

实现一个队列，队列初始为空，支持四种操作：

• push x – 向队尾插入一个数 x；
• pop – 从队头弹出一个数；
• empty – 判断队列是否为空；
• query – 查询队头元素。

现在要对队列进行 M 个操作，其中的每个操作 3 和操作 4 都要输出相应的结果。

输入格式

第一行包含整数 M，表示操作次数。

接下来 M 行，每行包含一个操作命令，操作命令为 push x，pop，empty，query 中的一种。

输出格式

对于每个 empty 和 query 操作都要输出一个查询结果，每个结果占一行。

其中，empty 操作的查询结果为 YES 或 NO，query 操作的查询结果为一个整数，表示队头元素的值。

数据范围

1≤M≤100000,
1≤x≤109,
所有操作保证合法。

输入样例

10
push 6
empty
query
pop
empty
push 3
push 4
pop
query
push 6
1
2
3
4
5
6
7
8
9
10
11

输出样例

NO
6
YES
4
1
2
3
4

不使用stl

#include <iostream>

using namespace std;

const int N=100010;

int hh,tt=-1;
int q[N];

int main ()
{
    int x,m;
    string op;
    
    cin>>m;
    while(m--)
    {
        cin>>op;
        if(op=="push")
        {
            cin>>x;
            q[++tt]=x;
        }
        else if(op=="pop")  hh++;
        else if(op=="empty")
        {
            if(hh<=tt)  cout<<"NO"<<endl;
            else cout<<"YES"<<endl;
        }
        else cout<<q[hh]<<endl;
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

使用stl

#include <iostream>
#include <queue>

using namespace std;

queue<int> q;

int main()
{
	int x,m;
    string op;
    
    cin>>m;
    while(m--)
    {
        cin>>op;
        if(op=="push")
        {
            cin>>x;
            q.push(x);
        }
        else if(op=="pop")  q.pop();
        else if(op=="empty")
        {
            if(q.size())  cout<<"NO"<<endl;
            else cout<<"YES"<<endl;
        }
        else cout<< q.front() <<endl;
    }
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

4.1 单调队列

与单调栈同理，单调队列是有单调性质的队列
如图对1， 3， 2， 4， 5 进行单调队列操作

要取最小值，要维护一个单调递增的队列

• 1入队时，队列为空，直接入队，队中元素：1
• 3入队时，队尾元素1小于3，直接入队，队中元素：1，3
• 2入队时，队尾元素3大于2，叉掉3，队尾元素1小于2，2入队，队中元素：1，2
• 4入队时，队尾元素2小于4，4入队，队中元素：1，2，4
• 5入队时，队尾元素4小于5，5入队，队中元素：1，2，4，5

4.2 应用实例

题目来源 ：acwing 154.滑动窗口

题目描述 :

给定一个大小为 n≤10^6 的数组。

有一个大小为 k 的滑动窗口，它从数组的最左边移动到最右边。

你只能在窗口中看到 k 个数字。

每次滑动窗口向右移动一个位置。

以下是一个例子：

该数组为 [1 3 -1 -3 5 3 6 7]，k 为 3。

你的任务是确定滑动窗口位于每个位置时，窗口中的最大值和最小值。

输入格式

输入包含两行。

第一行包含两个整数 n 和 k，分别代表数组长度和滑动窗口的长度。

第二行有 n 个整数，代表数组的具体数值。

同行数据之间用空格隔开。

输出格式

输出包含两个。

第一行输出，从左至右，每个位置滑动窗口中的最小值。

第二行输出，从左至右，每个位置滑动窗口中的最大值。

输入样例

8 3
1 3 -1 -3 5 3 6 7
1
2

输出样例

-1 -3 -3 -3 3 3
3 3 5 5 6 7
1
2

yxc’s解法

#include <iostream>
#include<algorithm>

using namespace std;

const int N=1000010;

int n,k;
int a[N],q[N]; 

int main()
{
	scanf("%d%d",&n,&k);
	
	for (int i=0;i<n;i++)	scanf("%d",&a[i]);
	
	int hh=0,tt=-1;
	for (int i=0;i<n;i++)
	{
		if(hh <= tt && q[hh] < i-k+1)	hh++;
		while(hh <= tt && a[q[tt]]>=a[i])	tt--;
		q[++tt]=i;
		
		if(i>=k-1)	printf("%d ",a[q[hh]]);
	}
	puts("");
	
	hh=0,tt=-1;
	for (int i=0;i<n;i++)
	{
		if(hh <= tt && q[hh] < i-k+1)	hh++;
		while(hh <= tt && a[q[tt]]<=a[i])	tt--;
		q[++tt]=i;
		
		if(i>=k-1)	printf("%d ",a[q[hh]]);
	}
	
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39