java数据结构与算法刷题-----LeetCode28：实现 strStr()

1. 思路分析

暴力解法，和KMP算法，具体看注释

2. 暴力解法代码
   

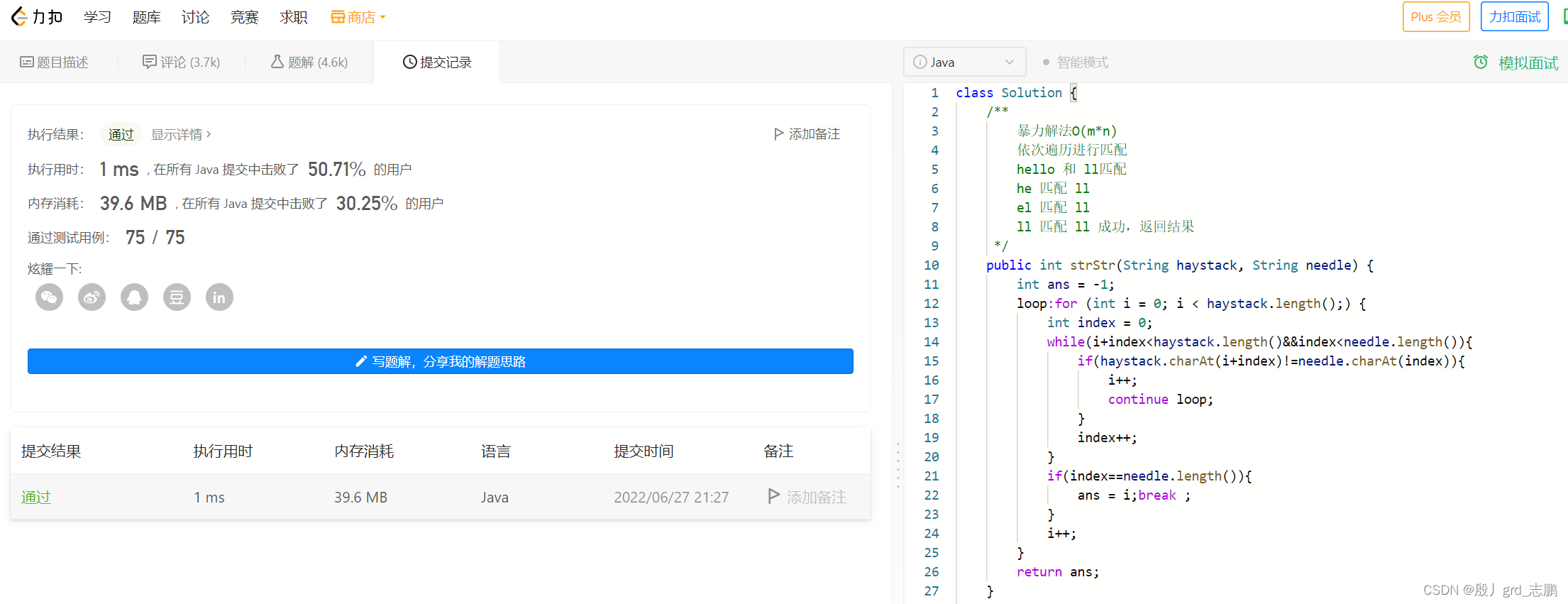
class Solution {
    /**
        暴力解法O(m*n)
        依次遍历进行匹配
        hello 和 ll匹配
        he 匹配 ll
        el 匹配 ll
        ll 匹配 ll 成功，返回结果
     */
    public int strStr(String haystack, String needle) {
        int ans = -1;
        loop:for (int i = 0; i < haystack.length();) {
            int index = 0;
            while(i+index<haystack.length()&&index<needle.length()){
                if(haystack.charAt(i+index)!=needle.charAt(index)){
                    i++;
                    continue loop;
                }
                index++;
            }
            if(index==needle.length()){
                ans = i;break ;
            }
            i++;
        }
        return ans;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

3. KMP解法代码
   

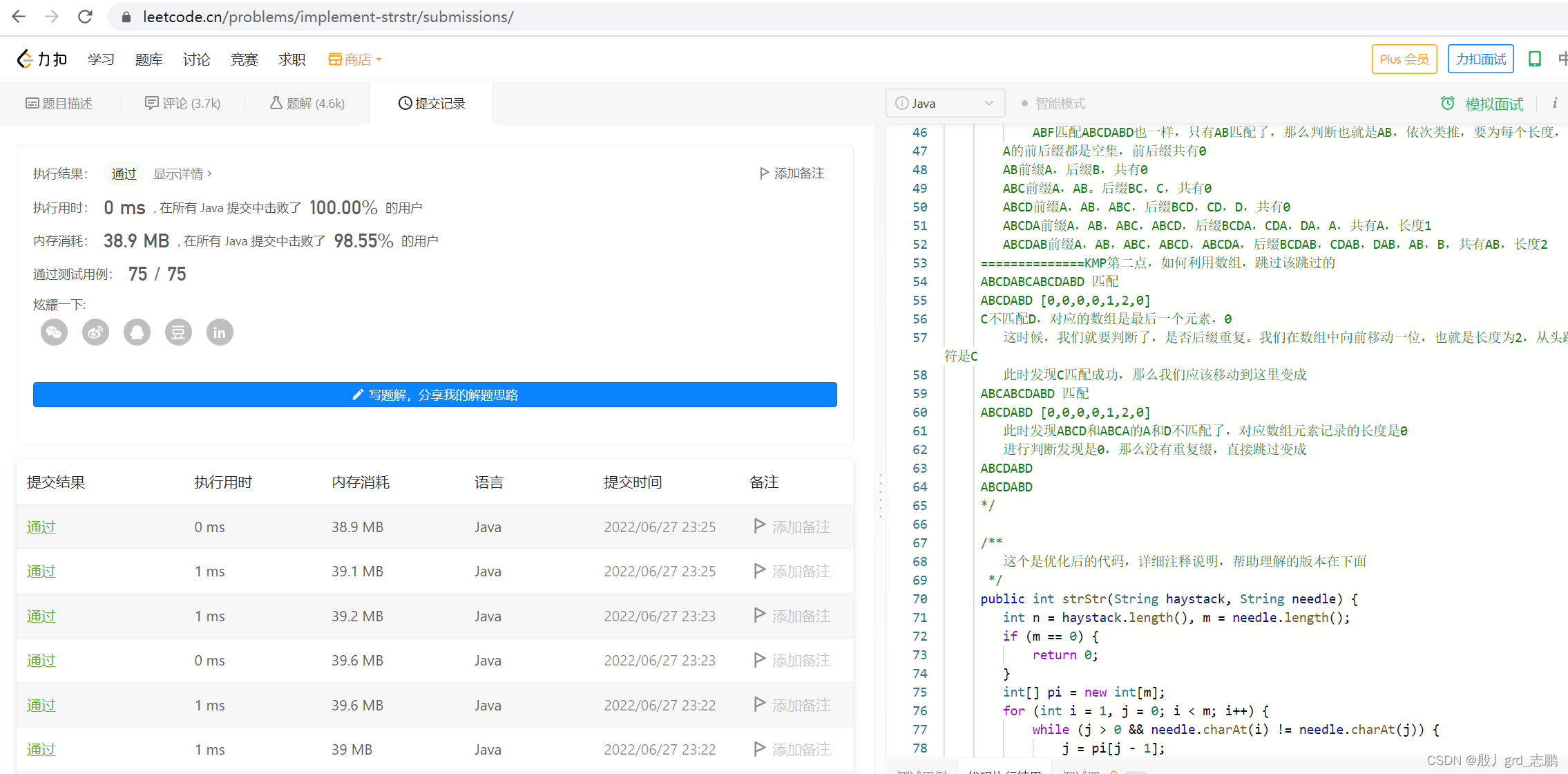
class Solution {
    /**
     KMP算法，重复出现的，不要重复比较，跳过它
     用一个数组来记录重复出现的次数
     ================暴力匹配的问题
     ABCDABEABCDABD 匹配 ABCDABD
     ABCDABEABCDABD
     ABCDABD    最后一个字母D不匹配E
     也就是说ABCDABE 这个串 肯定不匹配ABCDABD
     但是在未知的情况下，向后移一位，是否匹配，我们不知道，比如下面这种
     EABCDABD
     ABCDABD
     我们发现E不匹配，向后移一位
     ABCDABD
     ABCDABD 这就匹配了
     ====================所以暴力匹配中，我们不确定是否后移一位就匹配了，因此，只能一个个后移比较
     =============可以优化的点
     我们先看简单的匹配
     ABCDABE
     ABCDABD
     E和D不匹配，暴力解法，需要后移
     BCDABE
     ABCDABD
     此时，我们发现，又不匹配，如果我们想要匹配，最起码应该A开头吧，也就是说，再往后面移动，也没用，直到下一个A开头的
     CDABE
     ABCDABD
     DABE
     ABCDABD
     最后我们发现，BCD这三个开头，已经确定不匹配，没必要重复匹配，应该跳过，直接匹配下一个A
     ABE
     ABCDABD
     ==============KMP的解决思路
     ABCDABEABCDABD 匹配 ABCDABD
     ====首先第一点，我们先对ABCDABD这个子串做文章，判断每次如果不匹配，应该怎么跳过
     ABCDABE匹配ABCDABD，如果到D不匹配，应该直接变成ABE匹配ABCDABD，因为我们要找到下一个AB开头的
     ABCDEFGTTTTT匹配ABCDABD，如果第一次到E不匹配，应该直接变成EFGTTTTT匹配ABCDEFG，因为ABCD全部不匹配，直接跳过
     总结一下，可以发现，ABCDABD这个子串，出现两次AB，那么如果一直匹配到ABCDABD才发现不对，就应该直接跳到后面的AB继续匹配
     而如果没有匹配到出现重复字符，比如匹配到ABCD就发现不对了，那么就应该直接跳过ABCD
     ==============KMP第一点，如何记录（生成数组）
     是否有重复缀，应该用一个数组记录
     比如ABCDABD对应数组应该是[0,0,0,0,1,2,0],代表A重复，长度1，AB重复，长度为2.
     怎么算出来的呢？用前缀，后缀共同匹配法，就是把前缀和后缀列出来，看看共同拥有的元素长度
     ABCDABD 前缀，就是A，AB，ABC...,ABCDAB这样累加到倒数第二个，后缀是去掉第一个，依次递减，BCDAB，CDAB，DAB，AB，B
        然后共同的是AB，长度为2
        而实际过程中，并不是每次都可以匹配到ABCDABD这里，比如AF匹配ABCDABD，其实只匹配的A，那么前后缀判断也只有A
            ABF匹配ABCDABD也一样，只有AB匹配了，那么判断也就是AB，依次类推，要为每个长度，记录前后缀匹配度
        A的前后缀都是空集，前后缀共有0
        AB前缀A，后缀B，共有0
        ABC前缀A，AB。后缀BC，C，共有0
        ABCD前缀A，AB，ABC，后缀BCD，CD，D，共有0
        ABCDA前缀A，AB，ABC，ABCD，后缀BCDA，CDA，DA，A，共有A，长度1
        ABCDAB前缀A，AB，ABC，ABCD，ABCDA，后缀BCDAB，CDAB，DAB，AB，B，共有AB，长度2
     ==============KMP第二点，如何利用数组，跳过该跳过的
     ABCDABCABCDABD 匹配
     ABCDABD [0,0,0,0,1,2,0]
     C不匹配D，对应的数组是最后一个元素，0
        这时候，我们就要判断了，是否后缀重复。我们在数组中向前移动一位，也就是长度为2，从头跳过两个元素AB，发现对应字符是C
        此时发现C匹配成功，那么我们应该移动到这里变成
     ABCABCDABD 匹配
     ABCDABD [0,0,0,0,1,2,0]
        此时发现ABCD和ABCA的A和D不匹配了，对应数组元素记录的长度是0
        进行判断发现是0，那么没有重复缀，直接跳过变成
     ABCDABD
     ABCDABD
     */

     /**
        这个是优化后的代码，详细注释说明，帮助理解的版本在下面
      */
     public int strStr(String haystack, String needle) {
        int n = haystack.length(),m = needle.length();//为了更快的速度
         if(m==0) return 0;
        //1、kmp数组
        int[] kmpArr = new int[m];
        kmpArr[0] = 0;
        for (int i = 1,j = 0; i < m; i++) {
            //"ABCDABD"
            //"i***i"两个i对应的匹配成功，那么匹配成功长度+1，j++，长度为1。说明如果匹配到ABCDA，那么下次可以把ABCD跳过，末尾的A不可以跳过
            //" i***i"然后两个i位置又成功，j++，长度为2，也就是说匹配到了ABCDAB，下次ABCD可以跳过，末尾的AB不可以，因为重复了
            //最后，j = 2，i = 6，C不匹配D
            //j = kmp[j-1] 看看后移后的缀匹配程度，一直到匹配成功，或者j = 0，从开头重新匹配
            while(j>0 && needle.charAt(i)!=needle.charAt(j)) j = kmpArr[j-1];
            if(needle.charAt(i)==needle.charAt(j)) j++;//匹配成功，j长度+1
            kmpArr[i] = j;
        }
        //2、用kmp数组
        for (int i = 0,j = 0; i < n; i++) {
            //这里和上面代码一样，只不过原来是needle自己比，现在是haystack和needle比较
            while(j>0 && haystack.charAt(i)!=needle.charAt(j)) j = kmpArr[j-1];
            if(haystack.charAt(i)==needle.charAt(j)) j++;//匹配成功，j长度+1
            if(j==m) return i-j + 1;//匹配成功
        }
        return -1;//没成功
    }
    /**
        下面是容易理解的代码
     */
    // public int strStr(String haystack, String needle) {
    //     //先搞出kmpArr数组
    //     int[] kmpArr = kmpNext(needle);
    //     //用数组跳过没必要重复比较的
    //     return kmpSearch(haystack,needle,kmpArr);
    // }
    
    //第一步：获取到一个字符串(子串) 的部分匹配值表，KMP数组
    public static  int[] kmpNext(String dest) {
        //ABCDABD [0,0,0,0,1,2,0]
        int[] kmpArr = new int[dest.length()];//kmp数组，记录前后缀共同匹配长度
        kmpArr[0]=0;//单个字符，例如A的前后缀都是空集，前后缀共有0
        //i代表后缀下标，j代表前缀下标和数组对应下标
        for (int i = 1,j = 0; i < dest.length(); i++) {
            //i = 0 代表A字符，前后缀都是空串
            //i = 3 代表ABCD的D，j = 0，最前面的A
            //不相等，依然是0
            //i = 4 代表ABCDA，的A。j = 0代表最前面的A
            //前后缀相等了，但此时j = 0，说明前面没有前后缀匹配的，那么直接记录本次
            //j++ = 1 ， kmpArr[4] = 1
            //i = 5 代表ABCDAB，代表后缀B，j = 1代表前缀B
            //相等了，此时j>0,并且相等，那么直接j++即可
            //j = 2，kmpArr[5] = 2
            //i = 6 代表ABCDABD，代表后缀D，j = 2代表前缀C（ABC）
            //此时j>0,并且前后不相等，那么后缀D和C不匹配，需要尝试向前匹配
            //剩下他能匹配的，也就是，A和AB，对应j是0和1
            //j = kmpArr[j-1]，向前移动前缀，kmpArr[1] = 0
            //j = 0，前面没有了，判断前后缀现在是否相等
            //D 不等于 A 因此D这个后缀，没的匹配
            while(j>0&&dest.charAt(j)!=dest.charAt(i)){
                j=kmpArr[j-1];
            }
            if(dest.charAt(i)==dest.charAt(j)){
                j++;
            }
            //j 就是 长度
            kmpArr[i] = j;
        }
        return kmpArr;
    }

    /**第二步
     * kmp搜索
     *  依然进行匹配
     *  和上面一样，j就是匹配成功的前后缀共同长度
     *  
     */
    public static int kmpSearch(String str1, String str2, int[] kmpArr) {

        //遍历
        for(int i = 0, j = 0; i < str1.length(); i++) {
            //匹配不成功就跳过
            //需要处理 str1.charAt(i) ！= str2.charAt(j), 去调整j的大小
            //KMP算法核心点, 可以验证...
            //String str1 = "BBC ABCDAB ABCDABCDABDE";
            //    String str2 = "ABCDABD";
            //匹配表next=[0, 0, 0, 0, 1, 2, 0]
            //当i = 10,j = 6时，前面ABCDAB都匹配成功，但是现在空格比较D，不相等，此时说明不是子串
            //此时进入循环，j = 2，比较空格和C，不相等，再进入循环
            //j = 1,比较空格和B，不相等，再进入循环
            //j = 0，条件不满足，退出循环
            //下一次，将从空格后面继续匹配，避免前面比较过的，重复比较
            while( j > 0 && str1.charAt(i) != str2.charAt(j)) {
                j = kmpArr[j-1];
            }
            //匹配成功就继续
            if(str1.charAt(i) == str2.charAt(j)) {
                j++;
            }
            //和上面建立kmp数组一样，获得j，匹配成功的长度
            if(j == str2.length()) {//如果相等，匹配完全成功
                return i - j + 1;
            }
            //否则，匹配不成功
        }
        return  -1;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175

刷题一定要坚持，总结套路，不单单要把题做出来，要举一反三，也要参考别人的思路，学习别人解题的优点，找出你觉得可以优化的点。

1. 单链表解题思路：双指针、快慢指针、反转链表、预先指针

1. 双指针：对于单链表而言，可以方便的让我们遍历结点，并做一些额外的事
2. 快慢指针：常用于找链表中点，找循环链表的循环点，一般快指针每次移动两个结点，慢指针每次移动一个结点。
3. 反转链表：通常有些题，将链表反转后会更好做，一般选用三指针迭代法，递归的空间复杂度有点高
4. 预先指针：常用于找结点，比如找倒数第3个结点，那么定义两个指针，第一个指针先移动3个结点，然后两个指针一起遍历，当第一个指针遍历完成，第二个指针指向的结点就是要找的结点

2. 数组解题思路：双指针、三指针，下标标记

1. 双指针：多用于减少时间复杂度，快速遍历数组
2. 三指针：多用于二分查找，分为中间指针，左和右指针
3. 下标标记：常用于在数组范围内找东西，而不想使用额外的空间的情况，比如找数组长度为n，元素取值范围为[1,n]的数组中没有出现的数字，遍历每个元素，然后将对应下标位置的元素变为负数或者超出[1,n]范围的正数，最后没有发生变化的元素，就是缺少的值。
4. 差分数组：对差分数组求前缀和即可得到原数组

1. 用差值，作为下标，节省空间找东西。比如1900年到2000年，就可以定义100大小的数组，每个数组元素下标的查找为1900。
2. 前缀和数组，对于数组 [1,2,2,4]，其差分数组为 [1,1,0,2]，差分数组的第 ii个数即为原数组的第 i-1 个元素和第 i个元素的差值，也就是说我们对差分数组求前缀和即可得到原数组

5. 前缀和：假设有一个数组arr[1,2,3,4]。然后创建一个前缀和数组sum，记录从开头到每个元素区间的和。第一个元素是0。第二个元素，保存第一个和sum[1] = sum[0]+arr[0]，第二个元素，保存第二个和sum[2] = sum[1]+arr[1]

3. 栈解题思路：倒着入栈，双栈

1. 倒着入栈：适用于出栈时想让输出是正序的情况。比如字符串’abc’，如果倒着入栈，那么栈中元素是（c,b,a）。栈是先进后出，此时出栈，结果为abc。
2. 双栈：适用于实现队列的先入先出效果。一个栈负责输入，另一个栈负责输出。