第一章 矩阵与线性方程组（十三）

1.向量的相似度

模式分类
考虑M个类型的模式，它们分别记作$w_1，w_2,\cdot \cdot \cdot ,w_M$，编号随意。假定通过已知类型属性的观测样本，业已抽取出M个样本模式向量$s_1,s_2,\cdot \cdot \cdot ,s_M$。给定一任意的未知模式向量$x$，希望判断它归属于哪一类模式。这个问题称为模式分类，它是模式识别的基本问题之一。
模式分类的基本思想是将未知模式向量$x$同M个样本模式向量进行比对，看$x$4与哪一个样本模式向量最相似，并据此作出模式分类的判断。

• 假定$(x,s_1),(x,s_2),\cdot \cdot \cdot ,(x,s_M)$分别作为未知模式向量$x$和已知样本模式向量$s_1,s_2,\cdot \cdot \cdot ,s_M$之间的相似关系的符号。以$x$与$s_1,s_2$的相似关系为例，若
  &&(x,s_1)≤(x,s_2)&&
  则称未知模式向量$x$与样本模式向量$s_1$更相似。为了建立相似关系，需要定义相似度(similarity)或相异度(dissimilarity)。

距离函数

• 最简单和最直观的相似度是两个向量之间的Euclidean距离。未知模式向量$x$与第i个原象模式向量$s_i$之间的Euclidean距离记作$D(s_i,x)$，定义为
  $$D(s_i,x)=||x-s_i|{|}_2=(x-s;)T(\ae -si)$$
  称$s_i\in s_1,s_2,\dots ,s_M$是到$x$的近邻(即最近的邻居)，若
  $$D(s_i,x)=minD(s_k,x)，k=1,2,\dots ,M$$
• 作为一种广泛使用的分类法，近邻分类(nearestneighborclassification)法将未知类型的模式向量$x$归为它的近邻所属的模式类型。

除了Enclidean距离外，另外一个有用的距离函数是Mahalanobis距离。令
$$m=1/N\sum _{k=1}^N{s}_i$$
代表N个样本模式向量的均值向量，并使用
$$C=1/N\sum {i=1}^N(s_i-m)(s_i-m{)}^T$$
表示N个样本模式向量的协方差矩阵。

• 从未知模式向量$x$到均值向量$m$之间的Mahalanobis距离定义为
  $$D(m,x)=(x-m{)}^{T}C(x-m)$$
  类似地，从第$i$个样本模式向量$s_i$到均值向量$m$的Mahalanobis距离定义为
  $$D(m,s_i)=(s_i-m{)}^{T}C(s_i-m)$$
  根据近邻分类法，将未知模式向量$x$归为满足
  $$D(s_i,x)=min|D(s_k,x)-D(m,x)|,k=1,2,\dots ,N$$
  的近邻$s_i$所属的模式类型。

余弦函数
两个向量之间的相似度的测度不一定局限于距离函数。两个向量的夹角的余弦函数

也是相似度的一种有效测度。若$cos({\theta }_i)<cos({\theta }_j),\forall j\ne i$成立，则认为未知模式向量$x$与样本模式向量$s_i$最相似。
上式的变型：

称为Tanimoto测度，它泛应用于信息恢复、疾病分类、动物和植物分类等。

• 待分类的信号称为目标信号，分类通常是根据某种物理或几何概念进行的。令$X$为目标信号，$A_i$代表第$i$类目标的分类概念。于是，可以有类似于式的关系:
  $$(X,A_i)\le (X,A_j),\forall i,j$$
  这类有效关系一般用目标-概念距离(object-conceptdistance)$D(X,A_i)$描述。因此，若目标-概念距离$D(X,A_i)$最小，则将X归为第i类目标$C_i$。
  以上介绍了五种相似度:Euclidean距离、Mahalanobis距离、夹角余弦、Tanimoto测度以及目标-概念距离。

正交向量在移动通信中的应用

在移动通信中，总是有很多用户希望能够同亨一个发射媒介，进行无线通信。这种通信方式称为多址通信。多址通信的理论基础是若用户之间的信号可以做到正交，这些用户就可以同时共享一个发射媒介。

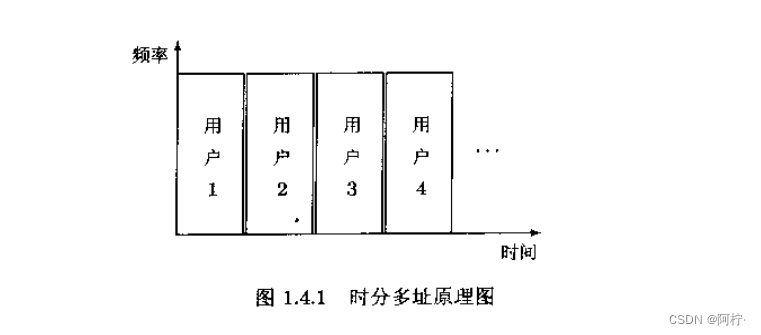
1.时分多址(TDMA)

用户共享整个频率信道，但每个用户被基站分配以不同的时区，并且相邻用户之间插有保护时隙，以使得他们的信号在时域没有任何重叠，从而实现用户信号之间(在时域)的正交，即有$<s_i(t),s_j(t)>=0,\forall i\ne j$,参见图14.1。由丁在用户i工作的时区，只有用户i的离散信号向量$s_i=[s_i(1),s_i(2),\dots ,s_i(N){]}^T$不为零，其他用户的离散信号均为零向量，所以时分多址实际上依靠向量正交$<s_i,s_j>=0$实现多址通信。

2.频分多址(FDMA)

所有用户可以同时进行通信，但每个用户被基站分配以不同的通信频道。即是说，所有用户信号在频域没有重叠，并且相邻用户的频道之间插有保护频隙，从而实现用户信号之间(在频域)的正交，即有$<S_i(f),S_j(f)>=0,\forall i\ne j$，如图1.4.2所示。

在用户i工作的频段，经过频率域的采样，只有用户i的频域信号为非零向量形式8=[S,(1),s;(2),…S(M)]T，其他用户的频域信号为零向量。因此，频分多址实际上依靠向量正交()=0实现多址通信。

3.跳频-码分多址(CDMA)

在同一个时区，每个用户被分配不同的频道，并目相邻频道之间播有保护额院。不同的时区，分配给用户的频道不同，即同一个用户的频道是跳跃变化的。图1.4.3以5个用户为例，画出了4次跳频的分配，其中，省画了相邻频道之间的保护频隙。

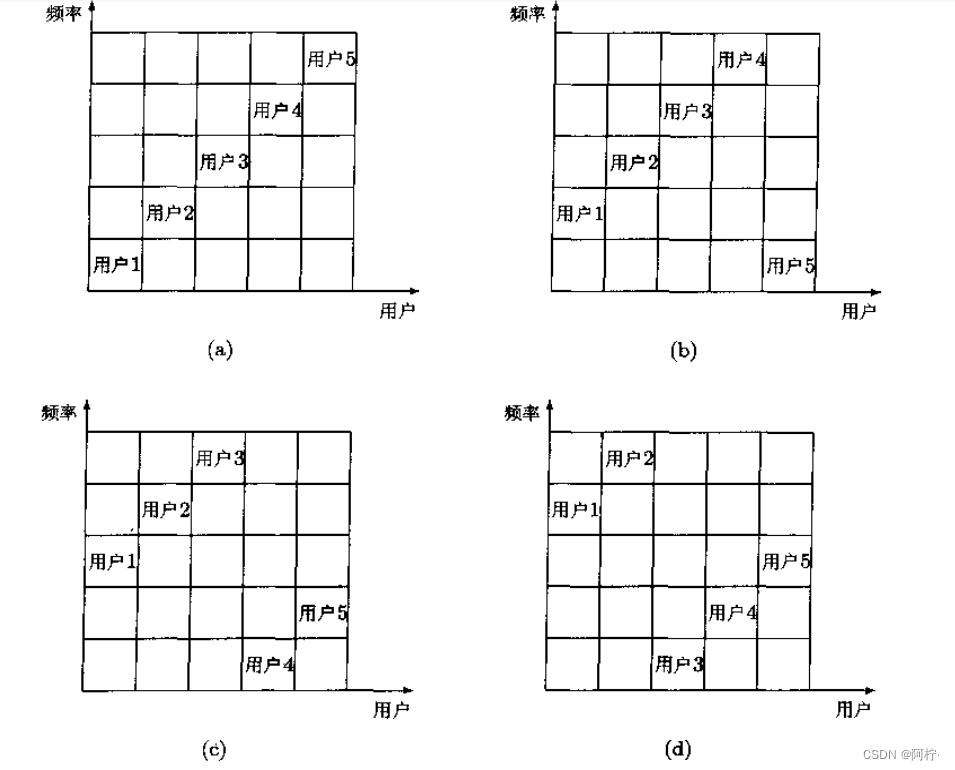
显然，只要能够保证在同一时区，各个用户的频道不重叠，其他各种形式的跳频都是可行的。

4直接序列-码分多址(DS-CDMA)

所有用户不仅可以同时进行通信，并且共享整个通信频道，但每个用户被基站分配以不同的扩频码向量$s_i=[s_i(1),s_i(2),\dots ,s_i(L){]}^T$，其中，L代表扩频增益。虽然这些扩频码在时间域或者频率域都是重叠的，但由于各个用户的扩频码为伪随机码，相互正交故码分多址依靠扩频码向量间的正交实现多址通信。