-
SVM——支持向量机(二)
4. 软间隔SVM
之前的描述都是基于数据是线性可分的情况。但是实际上并不能保证总是线性可分的;并且全部线性可分的分隔面并不一定是最好的,如下图所示,尽管实线实现了全部分隔,但其间隔很小,有轻微扰动时将会发生误判。相比之下,虚线的分隔面要更好一些。
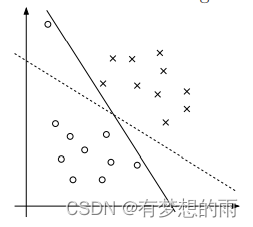
为使得模型能够适应非线性数据集,同时对离群点不那么敏感,将优化模型进行 l 1 l_1 l1 正则化如下:

5. 线性 SVM 算法步骤

6. 核方法
6.1 特征映射

6.2 特征的最小均方(LMS)

但是,当变量的特征维数迅速扩大时,其特征的组合数也会急速扩大,如令 ϕ ( x ) \phi(x) ϕ(x) 是三次幂之下的特征组合时,当 x x x 只有三个维度,那么 ϕ ( x ) = [ 1 , x 1 , x 2 , x 1 2 , x 1 x 2 , x 1 x 3 , x 2 2 , x 2 x 3 , x 3 2 , x 1 2 x 2 , x 1 2 x 3 , x 2 2 x 1 , ⋯ , x 3 3 ] \phi(x)=[1,x_1,x_2,x_1^2,x_1x_2,x_1x_3,x_2^2,x_2x_3,x_3^2,x_1^2x_2,x_1^2x_3,x_2^2x_1,\cdots,x_3^3] ϕ(x)=[1,x1,x2,x12,x1x2,x1x3,x22,x2x3,x32,x12x2,x12x3,x22x1,⋯,x33],即维度 d d d 的三次幂 d 3 d^3 d3。此时,模型的参数量和计算量都将急剧增加。
6.3 核方法
6.3.1 核方法的推导
为避免大量运算,考虑使用核方法,如下:

即,使用向量内积 ⟨ ϕ ( x ( j ) , x ( i ) ) ⟩ \langle\phi(x^{(j)},x^{(i)}) \rangle ⟨ϕ(x(j),x(i))⟩ 替代特征的组合运算,从而大幅降低计算复杂度。6.3.2 两个优点
- 在每次参数更新前需提前计算 ⟨ ϕ ( x ( j ) , x ( i ) ) ⟩ \langle\phi(x^{(j)},x^{(i)}) \rangle ⟨ϕ(x(j),x(i))⟩ ,将时间复杂度 降至 O ( p ) O(p) O(p);
- 内积 ⟨ ϕ ( x ( j ) , x ( i ) ) ⟩ \langle\phi(x^{(j)},x^{(i)}) \rangle ⟨ϕ(x(j),x(i))⟩ 的计算是便捷有效的,无需分别计算 ϕ ( x ( i ) ) \phi(x^{(i)}) ϕ(x(i)),直接降复杂度降至 O ( d ) O(d) O(d),因为:
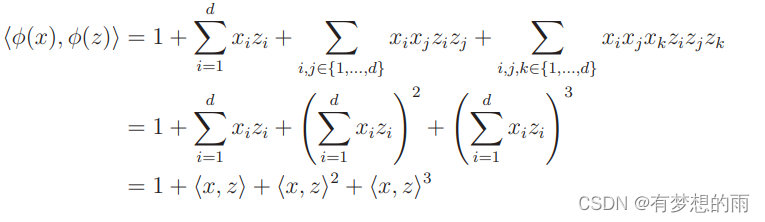
6.3.3 核方法的步骤

6.4 核方法的性质
6.4.1 多项式核
从上述推导中可以看出,核方法只需要保证这个特征映射 ϕ \phi ϕ 是存在的,而不需要显式的写出这个特征映射。即只需说明,是否存在这样一个特征映射 ϕ \phi ϕ,使得 K ( x , z ) = ⟨ ϕ ( x , z ) ⟩ = ϕ ( x ) T ϕ ( z ) K(x,z)=\langle\phi(x,z) \rangle=\phi(x)^T\phi(z) K(x,z)=⟨ϕ(x,z)⟩=ϕ(x)Tϕ(z) 对所有的 x , z x, z x,z 都成立。
如果存在,则可以将选择特征映射 ϕ \phi ϕ 的工作转换为 选择 核函数 K K K 的工作。这样做的好处在于,不要显式的特征映射写出来,而是只需要知道存在即可。具体例子如下:

更一般的,对于核 K ( x , z ) = ( x T z + c ) k K(x,z)=(x^Tz+c)^k K(x,z)=(xTz+c)k,对应于从 1 1 1 维到 d + k d+k d+k 维的特征映射。其工作空间是 O ( d k ) O(d^k) O(dk) ,但核 K ( x , z ) K(x,z) K(x,z) 的计算只需 O ( d ) O(d) O(d) 的时间。6.4.2 高斯核
核是一种相似性度量。
若 ϕ ( x ) \phi(x) ϕ(x) 和 ϕ ( z ) \phi(z) ϕ(z) 很接近,那么 K ( x , z ) = ϕ ( x ) T ϕ ( z ) K(x,z)=\phi(x)^T\phi(z) K(x,z)=ϕ(x)Tϕ(z) 就会很大;相反的,若 ϕ ( x ) \phi(x) ϕ(x) 和 ϕ ( z ) \phi(z) ϕ(z) 差异很大,那么 K ( x , z ) = ϕ ( x ) T ϕ ( z ) K(x,z)=\phi(x)^T\phi(z) K(x,z)=ϕ(x)Tϕ(z) 就会变小。因此可以将 K ( x , z ) K(x,z) K(x,z) 视为 ϕ ( x ) \phi(x) ϕ(x) 和 ϕ ( z ) \phi(z) ϕ(z) 的相似性的度量。
此时,选择 高斯核,此时,若 x x x 和 z z z 很接近,那么趋于1;若差距很大,则趋于 0 。高斯核对于一个无限维的特征映射。
K ( x , z ) = e x p ( − ∣ ∣ x − z ∣ ∣ 2 2 σ 2 ) \displaystyle K(x,z)=exp(-\frac{||x-z||^2}{2\sigma^2}) K(x,z)=exp(−2σ2∣∣x−z∣∣2)6.4.3 一个核函数有效的充要条件

7 非线性SVM——核方法
在线性支持向量机学习的对偶问题中,用核函数 K ( x , z ) K(x,z) K(x,z) 替代内积,求解得到的就是非线性支持向量机。
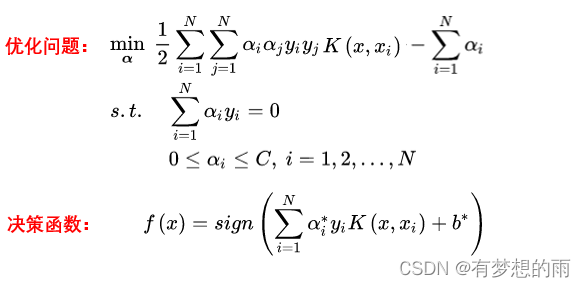
-
相关阅读:
图书管理系统
【DSP】【第四篇】如何生成bin和dat文件
人工智能前沿——AI技术在医疗领域的应用(二)
点云从入门到精通技术详解100篇-基于路侧激光雷达的交通目标感知方法与实现
大数据认知
OpenGL LUT滤镜算法解析
安防监控/视频汇聚/云存储/AI智能视频分析平台EasyCVR下级海康设备无法级联是什么原因?
史上最全,接口测试-用例设计总结(案例分析实例)一篇策底打通...
深入理解rtmp(一)之开发环境搭建
3.加载天地图
- 原文地址:https://blog.csdn.net/qq_41536160/article/details/125525489