【20220629】【信号处理】（平稳随机信号）自相关函数性质的证明过程

【20220629】【信号处理】（平稳随机信号）自相关函数性质的证明过程

目录

1. 偶函数

2. tau=0 处取得最大值

3. 周期函数的自相关函数也是周期函数，且周期和原函数相同

4. 对于非周期信号，当 tau 趋于无穷大时，自相关函数趋于信号平均值的平方

        由之前的文章《自相关函数的定义、计算方法及应用》可以知道，自相关函数有几个常用的性质：
① 自相关函数是偶函数；
② 自相关函数在时延为 0 时取得最大值；
③ 周期函数的自相关函数也是周期函数；
④ 对于非周期函数，当时延趋于无穷时，自相关函数趋于信号均值的平方。


        下文将对这四点性质进行理论证明 （本文假定信号是平稳随机信号）。

1. 偶函数

$R(-\tau)=E[x(t)x(t-\tau)]$

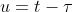做变量代换，令 $u = t-\tau$ ，则有：

$R(-\tau)=E[x(u+\tau)x(u)]=R(\tau)$

        因此，自相关函数为偶函数。

2. tau=0 处取得最大值

利用任何非负函数的期望恒为非负值的性质，则有：

$E[(x(t)-x(t+\tau))^2]\ge0$

$E[x^{2}(t)-2x(t)x(t+\tau)+x^{2}(t+\tau)]\ge0$

$E[x^2(t)]-2E[x(t)x(t+\tau)]+E(x^2(t+\tau))\ge0$

若  为平稳过程，则有：

$E[x^2(t)]=E[x^2(x+\tau)]=R_{x,x}(0)$

则有：

$2R(0)-2R(\tau)\ge0$

即：

$R(0)\ge R(\tau)$

        因此，自相关函数在 $\tau=0$ 处取得最大值，且为平稳随机过程的 “平均交流功率” 。

3. 周期函数的自相关函数也是周期函数，且周期和原函数相同

$\begin{align} R(t+\tau)&=E[x(t)x(t+\tau+T)]=E[x(t)x((t+T)+\tau)]\nonumber\\ &=E[x(t)x(t)+\tau)]\nonumber\\ &=R(\tau)\nonumber \end{align}$

4. 对于非周期信号，当 tau 趋于无穷大时，自相关函数趋于信号平均值的平方

$\lim\limits_{\left|\tau\rightarrow+\infty\right|}R(\tau)=R(\infty)=\mu^2_x$

        证明：

$\begin{align} \lim\limits_{\left|\tau\right|\rightarrow+\infty}R(\tau)=\lim\limits_{\left|\tau\right|\rightarrow+\infty}E[x(t)x(t+\tau)]\nonumber \end{align}$

随着 $\left|\tau\right|$ 增大， $x(t), x(t+\tau)$ 之间的相关性会逐渐减弱，当 $\left|\tau\right|\rightarrow+\infty$ 时， $x(t), x(t+\tau)$ 趋于独立，则有：

$\begin{align} \lim\limits_{\left|\tau\right|\rightarrow+\infty}R(\tau)&=\lim\limits_{\left|\tau\right|\rightarrow+\infty}E[x(t)x(t+\tau)]\nonumber \\ &=\lim\limits_{\left|\tau\right|\rightarrow+\infty}E[x(t)]E[x(t+\tau)]\nonumber\\ &=\mu^2_x \nonumber\end{align}$

        证毕！
相关阅读:
【Java】poi-tl实现导出Word模板并动态渲染数据
 shell脚本简介
 测试人如何打造简历化思维？
从裸机启动开始运行一个C++程序（十）
流程自动化
 eNSP学习——静态路由及默认路由基本配置
 每日亿题之20220904
java多线程使用详解与案例，超详细
 深度学习入门（二十三）卷积神经网络——图像卷积
 linux使用源码安装软件
原文地址：https://blog.csdn.net/weixin_40583722/article/details/125526367

1. 偶函数

2. tau=0 处取得最大值

3. 周期函数的自相关函数也是周期函数，且周期和原函数相同

4. 对于非周期信号，当 tau 趋于无穷大时，自相关函数趋于信号平均值的平方