• 数学知识复习：第二型曲线积分

    0 引出

            设一质点在力F的作用下，沿曲线C运动，力F在曲线C的各点处的方向和大小可以是不同的，F(x,y)是一个向量函数，那么如何计算这个质点在变力F的作用下，沿曲线C由点A运动到点B所做的功呢？

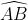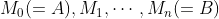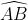             \widehat{AB} 弧上从A到B依次取点M_0(=A),M_1,\cdots,M_{n}(=B)，于是 \widehat{AB}被分割成n段小弧\widehat{M_{i-1}M_i} .

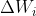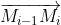            我们先考虑力F沿着小弧\widehat{M_{i-1}M_i}运动所做的功\Delta W_i。在小弧\widehat{M_{i-1}M_i}上任取一点(\xi_i,\eta_i)，以(\xi_i,\eta_i)处的力F(\xi_i,\eta_i)作为 小弧\widehat{M_{i-1}M_i} 上各点的力。同时近似地认为 小弧\widehat{M_{i-1}M_i} 是直线段\overrightarrow{M_{i-1}M_i}。

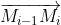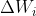            我们以内积 F(\xi_i,\eta_i) ·\overrightarrow{M_{i-1}M_i}作为力F沿着小弧\widehat{M_{i-1}M_i}运动所做的功\Delta W_i的近似式。

            所以和式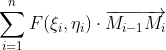\sum_{i=1}^n F(\xi_i,\eta_i) \cdot \overrightarrow{M_{i-1}M_i}是所求功W的近似值。

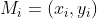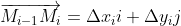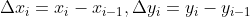
             如果F(x,y)=P(x,y)i+Q(x,y)j, M_i=(x_i,y_i),那么\overrightarrow{M_{i-1}M_i}=\Delta x_i i+\Delta y_ij ，其中\Delta x_i=x_i-x_{i-1}, \Delta y_i=y_i-y_{i-1}

             所以\sum_{i=1}^n F(\xi_i,\eta_i) \cdot \overrightarrow{M_{i-1}M_i}=\sum_{i=1}^n [P(\xi_i,\eta_i)\Delta x_i+Q(\xi_i,\eta_i)\Delta y_i]

     1 定义

     

     2 性质

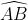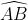    （1）F，G在\widehat{AB} 上连续，a,b是常数，则有\int_{\widehat{AB}}[aF+bG]\cdot ds=a\int_{\widehat{AB}}F\cdot ds+b\int_{\widehat{AB}}G\cdot ds

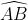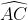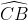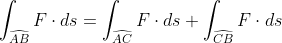
    （2）如果曲线\widehat{AB} 上一点C将积分路线\widehat{AB}  分成两段\widehat{AC},\widehat{CB},则\int_{\widehat{AB}}F\cdot ds=\int_{\widehat{AC}}F\cdot ds+\int_{\widehat{CB}}F\cdot ds

    （3）\int_{\widehat{AB}}F\cdot ds=-\int_{\widehat{BA}}F\cdot ds

     

     3 计算方法

    也是转化成定积分

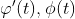    如果曲线C的参数方程是x=\varphi(t),y=\phi(t)，当参数t从α变到β时，点(x,y)从A变到B（此时不一定α比β小！）；同时\varphi'(t),\phi(t)在α和β之间连续，F在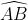\widehat{AB}上连续（即P,Q在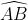\widehat{AB}上连续）

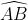    则第二型曲线积分\int_{\widehat{AB}}F\cdot ds=\int_{\widehat{AB}}P\cdot dx+\int_{\widehat{AB}}Q\cdot dy 可以转化为

    \int_\alpha^\beta[P(\varphi(t),\phi(t))\varphi'(t)+Q(\varphi(t),\phi(t))\phi'(t)]dt

    如果\widehat{AB}弧的方程为y=y(x)，其中x从α变化到β，那么有：

     \int_\alpha^\beta[P(x,y(x))+Q(x,y(x))y'(x)]dx

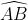     如果\widehat{AB}弧的方程为x=x(y)，其中y从c变化到d，那么有：

     \int_c^d[P(x(y),y)x'(y)+Q(x(y),y)]dy 

     4 第一型曲线积分和第二型曲线积分的关系

     

     

  • 相关阅读:
    React: 如何保证中断之后的状态？
    java基础练习--基础语法
    [极客大挑战 2019]HardSQL1
    GO: 快速升级Go版本
    自动化测试用例设计-软件测试基本概念解析
    html table 如何导出为excel表格案例分享
    【数据结构】链表面试题
    复盘-----vue
    Mycat2 分布式数据库中间件
    android ViewPager + Fragment + Tablayout 实现嵌套页面导航
  • 原文地址：https://blog.csdn.net/qq_40206371/article/details/125520610