matlab习题 —— 图像绘制练习

matlab系列文章：👉 目录 👈

文章目录

• • 一、题目
  • 二、解答
  • • 题一
    • • ① 读取附件1 sd.xlsx，以相邻两列数据绘制散点图并标注
      • ② 以第 1，2，4 列数据绘制空间散点图
    • 题二
    • • ① $y=sinx$，$y=cosx$ 在同一幅图
      • ② $y=sinx$，$y=cosx$ 在同一幅图不同窗口
    • 题三
    • • ① 竖直柱状图
      • ② 水平柱状图
      • ③ 立体柱状图
      • ④ 饼状图
    • 题四
    • • ① 绘制空间曲线 $x=e^{0.3t}sint$，$y=e^{0.3t}cost$，$z=e^{0.3t}$，$t\in [0,6\pi ]$
    • 题五
    • • ① 使用 mesh、surf 绘制曲面$$z=f(x,y)=\frac{sin\sqrt{x^2+y^2}}{\sqrt{x^2+y^2}},x.y\in [-10,10]$$
      • • Ⅰ、mesh 图像
        • Ⅱ、surf 图像
    • 题六
    • • ① 绘制上半球面 $z=\sqrt{4-x^2-y^2}$ 与锥面 $z+2=\sqrt{x^2+y^2}$ 所围成的立体
    • 题七
    • • ① 平面 $z=2x-3y$ 截马鞍面 $z=x^2-2y^2$

一、题目

• (1) 读取附件1 sd.xlsx，以相邻两列数据绘制散点图并标注；以第 1，2，4 列数据绘制空间散点图
• (2) 根据下面图形写出作图语句
  • ① $y=sinx$，$y=cosx$ 在同一幅图；
  • ② $y=sinx$，$y=cosx$ 在同一幅图不同窗口
• (3) 数组 $[2,5,10,12,13,7,2,10,4,6,8,8,4,7,8]$ 作竖直、水平、立体柱状图、饼状图
• (4) 绘制空间曲线 $x=e^{0.3t}sint$，$y=e^{0.3t}cost$，$z=e^{0.3t}$，$t\in [0,6\pi ]$
• (5) 使用 mesh、surf 绘制曲面$$z=f(x,y)=\frac{sin\sqrt{x^2+y^2}}{\sqrt{x^2+y^2}},x.y\in [-10,10]$$
• (6) 绘制上半球面 $z=\sqrt{4-x^2-y^2}$ 与锥面 $z+2=\sqrt{x^2+y^2}$ 所围成的立体
• (7) 平面 $z=2x-3y$ 截马鞍面 $z=x^2-2y^2$

二、解答

>> [num1]=xlsread('F:\sd.xlsx',1,'A1:B191')
>> [num2]=xlsread('F:\sd.xlsx',1,'D1:E191')
>> [num3]=xlsread('F:\sd.xlsx',1,'G1:H40')
1
2
3

题一

① 读取附件1 sd.xlsx，以相邻两列数据绘制散点图并标注

>> scatter(num1(:,[1]),num1(:,[2]),[],'b','filled')
>> hold on
>> scatter(num2(:,[1]),num2(:,[2]),[],'r','filled')
>> hold on
>> scatter(num3(:,[1]),num3(:,[2]),[],'black','filled')
>> title('shu ju A B C san dian tu')
>> legend('shu ju zu A','shu ju zu B','shu ju zu C')
1
2
3
4
5
6
7

② 以第 1，2，4 列数据绘制空间散点图

>> scatter3(num1(:,[1]),num1(:,[2]),num2(:,[1]),'filled')
1

题二

① $y=sinx$，$y=cosx$ 在同一幅图

>> x = 0:0.01:2*pi
>> y1 = sin(x)
>> y2 = cos(x)
>> plot(x,y1,x,y2)
>> title('The graph of sinx and cosx','color','b')
>> legend('y=cosx','y=sinx')
1
2
3
4
5
6

② $y=sinx$，$y=cosx$ 在同一幅图不同窗口

>> subplot(1,2,1)
>> plot(x,y1)
>> title('y=sinx')
>> box off
>>
>> subplot(1,2,2)
>> plot(x,y2)
>> title('y=cosx')
>> box off
1
2
3
4
5
6
7
8
9

题三

数组 $[2,5,10,12,13,7,2,10,4,6,8,8,4,7,8]$

>> % 读数据
>> data = [2,5,10,12,13,7,2,10,4,6,8,8,4,7,8]
1
2

① 竖直柱状图

>> bar(data)
1

② 水平柱状图

>> barh(data)
1

③ 立体柱状图

>> bar3(data)
1

④ 饼状图

>> pie(data)
1

题四

① 绘制空间曲线 $x=e^{0.3t}sint$，$y=e^{0.3t}cost$，$z=e^{0.3t}$，$t\in [0,6\pi ]$

>> t = 0:0.01:6*pi
>> x = exp(0.3*t).*sin(t)
>> y = exp(0.3*t).*cos(t)
>> z = exp(0.3*t)
>> plot3(x,y,z)
1
2
3
4
5

题五

① 使用 mesh、surf 绘制曲面$$z=f(x,y)=\frac{sin\sqrt{x^2+y^2}}{\sqrt{x^2+y^2}},x.y\in [-10,10]$$

>> x = -10:0.25:10
>> y = -10:0.25:10
>> [x,y] = meshgrid(x,y)
>> R = (x.^2+y.^2).^(1/2)
>> z = sin(R)./R
>>
>> mesh(x,y,z)
>>
>>
1
2
3
4
5
6
7
8
9

Ⅰ、mesh 图像

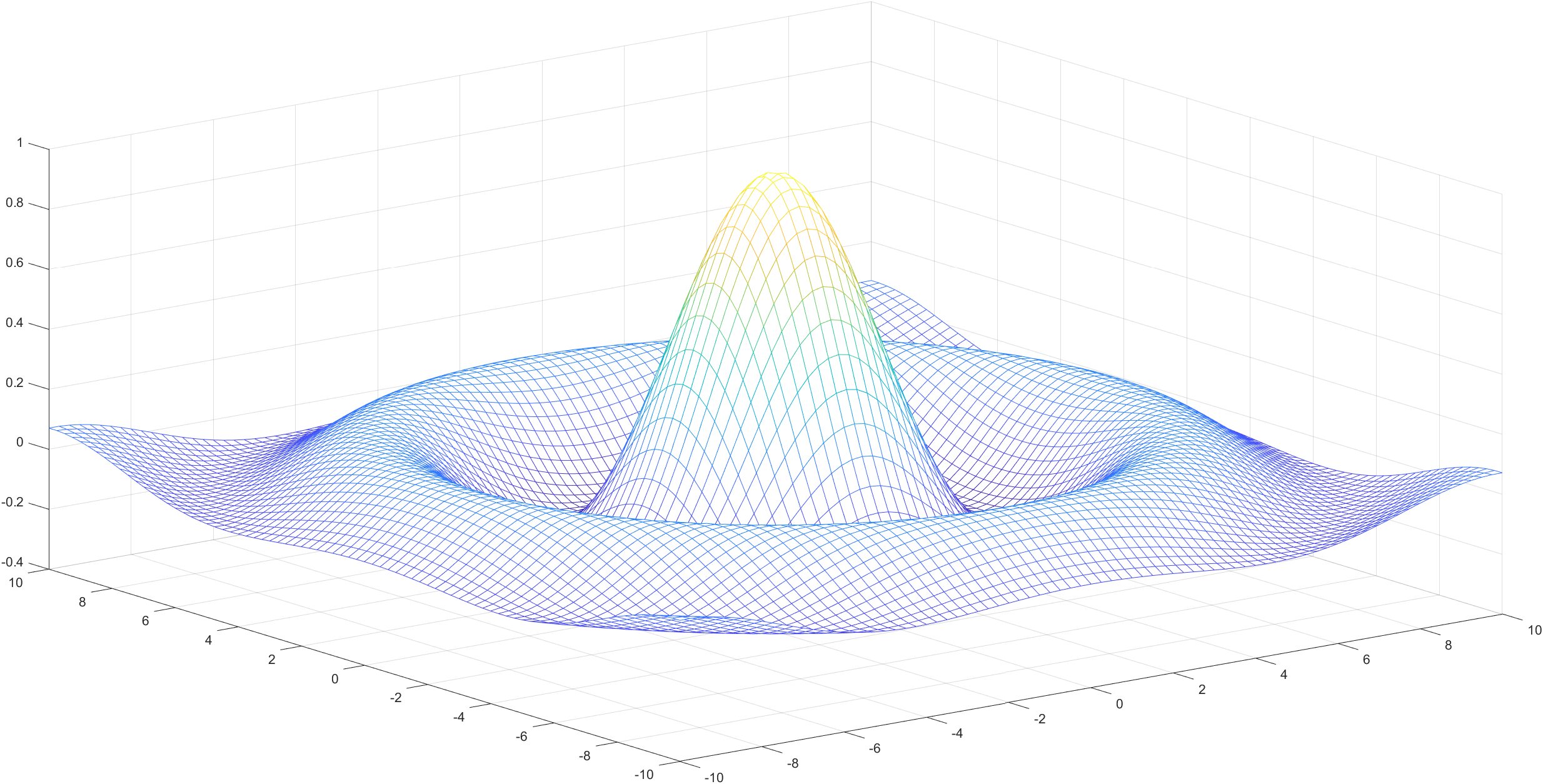
Ⅱ、surf 图像

题六

① 绘制上半球面 $z=\sqrt{4-x^2-y^2}$ 与锥面 $z+2=\sqrt{x^2+y^2}$ 所围成的立体

>> x=-2:0.01:2;
>> y=-2:0.01:2;
>> [x,y]=meshgrid(x,y);
>> z1=real(sqrt(4-x.^2-y.^2));
>> z2=sqrt(x.^2+y.^2)-2;
>> surf(x,y,z1),shading flat
>> hold on
>> z2(z2>0)=NaN;
>> surf(x,y,z2),shading flat
1
2
3
4
5
6
7
8
9

题七

① 平面 $z=2x-3y$ 截马鞍面 $z=x^2-2y^2$

>> x = -20:.1:20
>> y = -20:.1:20
>> [x,y]=meshgrid(x,y)
>> z1 = 2*x-3*y
>> z2 = x.^2-2*y.^2
>> mesh(x,y,z1)
>> hold on
>> mesh(x,y,z2)
1
2
3
4
5
6
7
8