行测-图形推理-3-对称图形类

当观察到图形都是较规整但元素组成凌乱时，可以考虑对称性质的考察。

本篇将主要针对考察对称性质的题目，对称的考查方式有以下几个方面：

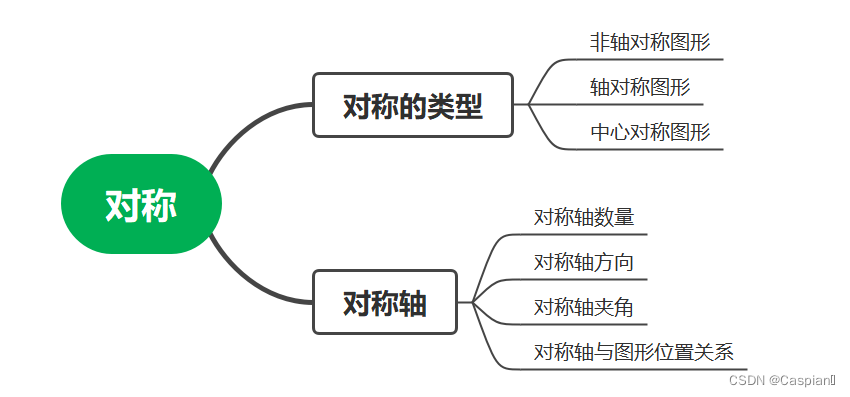
下面针对不同类型给出例题：

目录

一、对称的类型

二、对称轴 

1.对称轴数量

2.对称轴方向

3.对称轴夹角

4.对称轴与图形位置关系

---

一、对称的类型

（1）

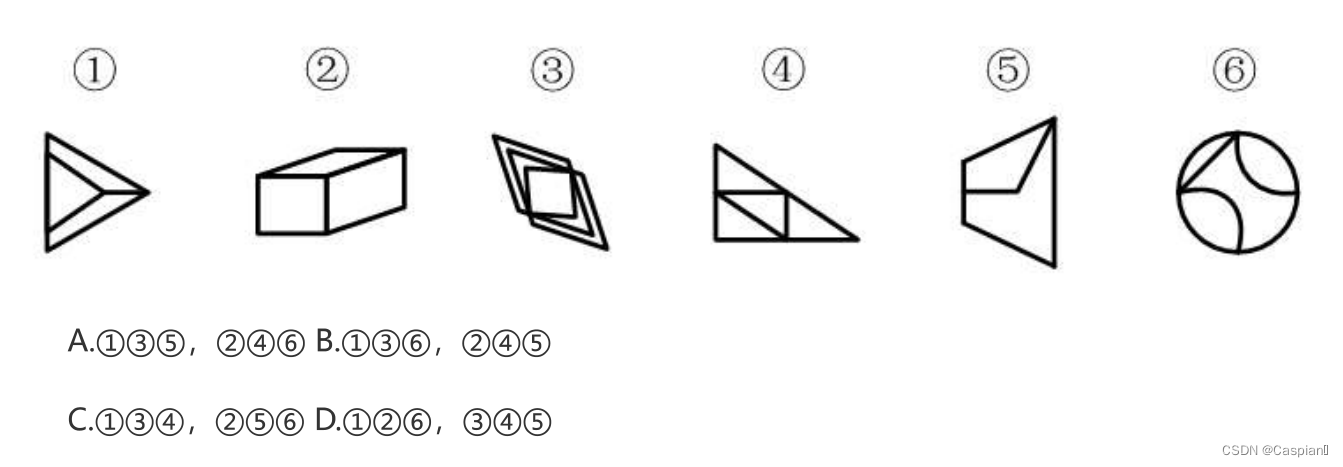
1，3，6为对称图形；2，4，5为非对称图形。

（2）

 图形依次为轴对称、中心对称、轴对称、中心对称、轴对称，下一个选择中心对称图形C。

 （3）

 1，2，4为轴对称图形；3，5，6为中心对称图形。

二、对称轴 

1.对称轴数量

（1）

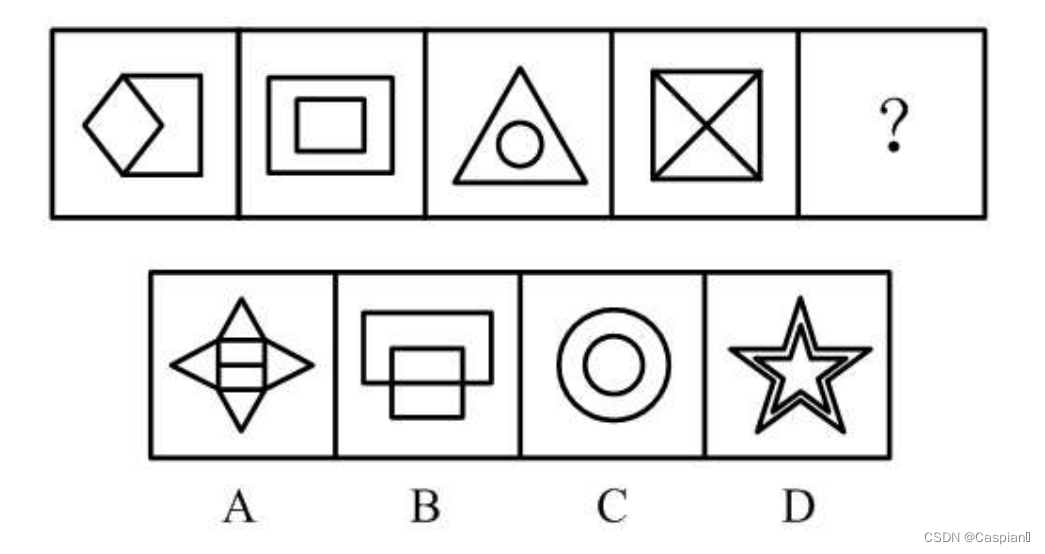
对称轴数量为1，2，3，4，故选择对称轴数量为5的D。

（2）

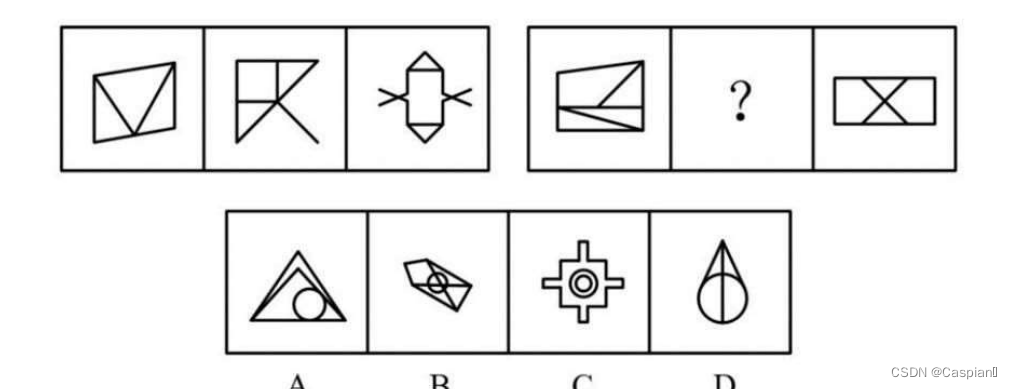
 第一组图形对称轴数量为0，1，2；故在第二组图形中选对称轴数量为1且对称轴方向指向左上方45度的B。

 （3）

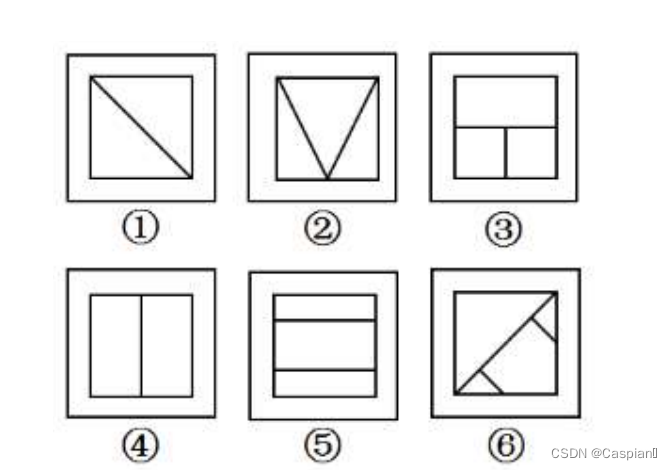
 1，4，5有两条对称轴；2，3，6有一条对称轴。

2.对称轴方向

（1）

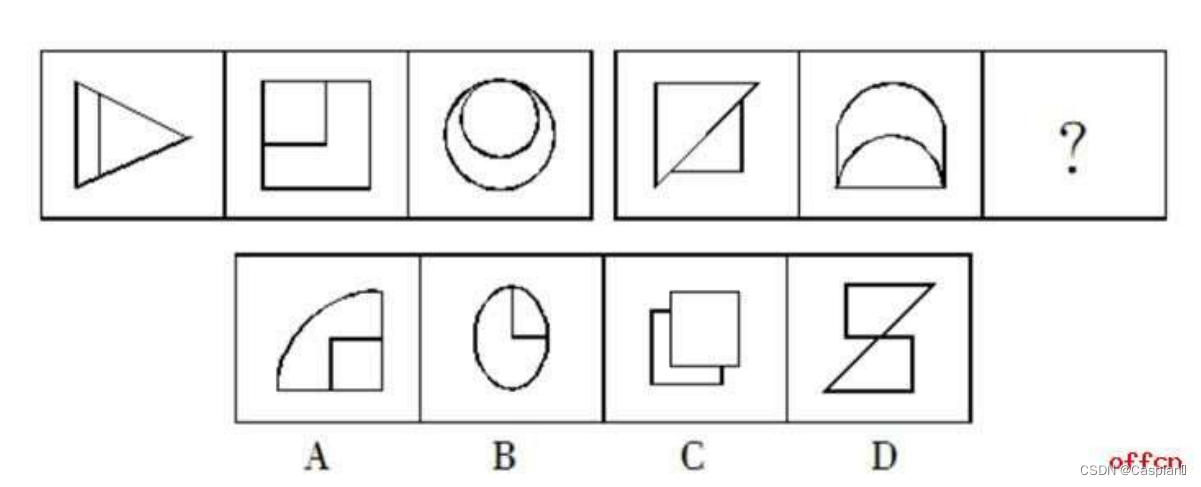
第一组图形对称轴依次顺时针旋转45度；故选C（B为椭圆）。

（2）

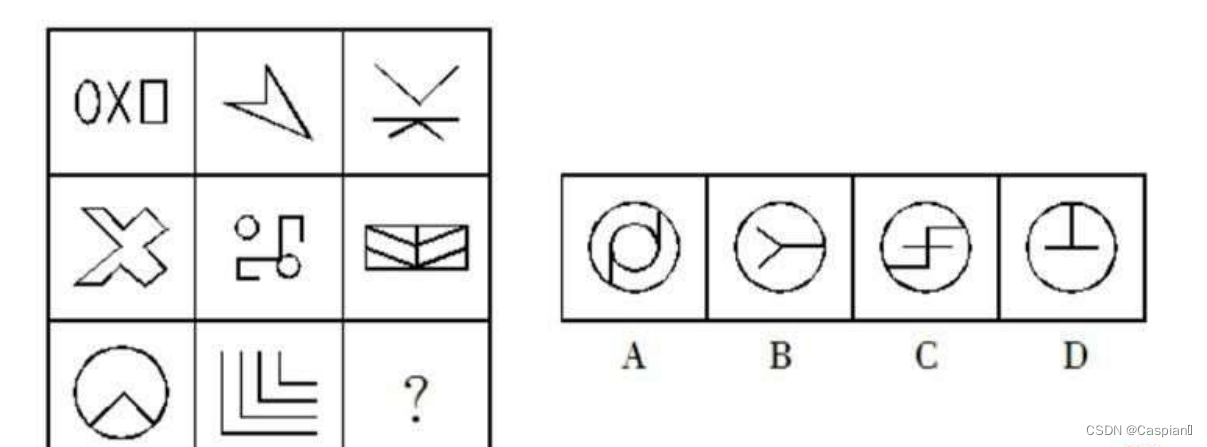
按行寻找规律，对称轴方向顺时针旋转45度。故选B。

 （3）

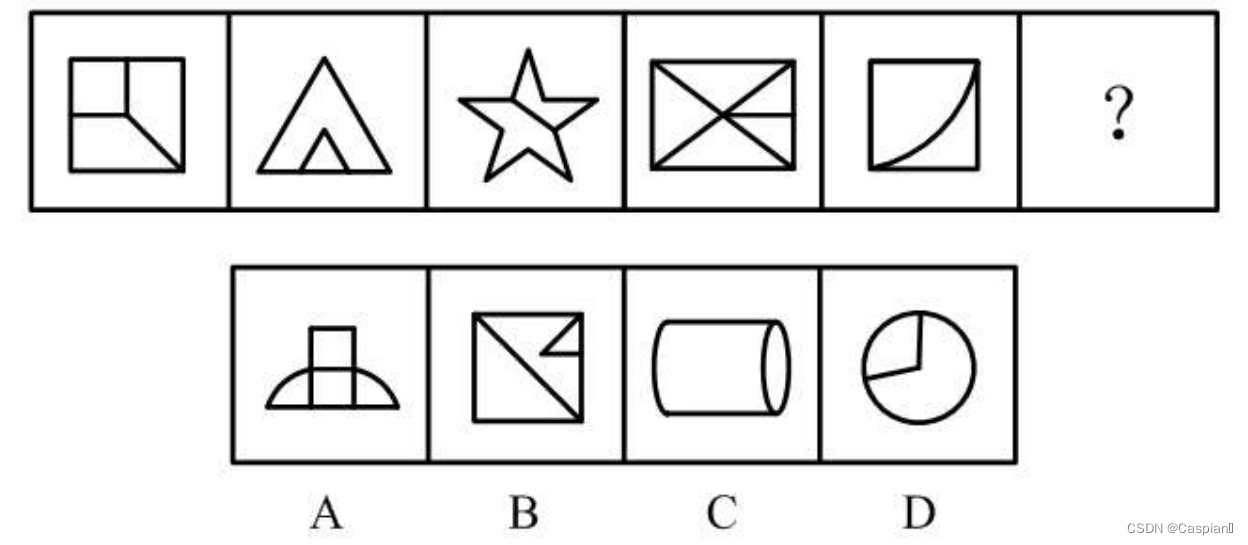
对称轴方向依次顺时针旋转45度，故选A。

 （4）

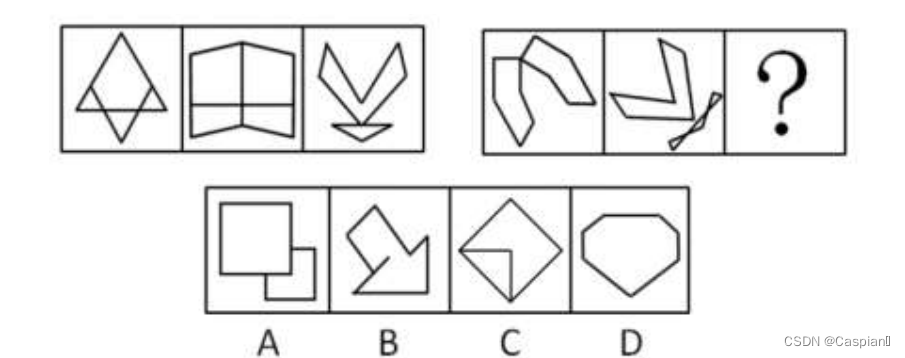
每一组图形对称轴方向一致，故选A。

 

3.对称轴夹角

（1）

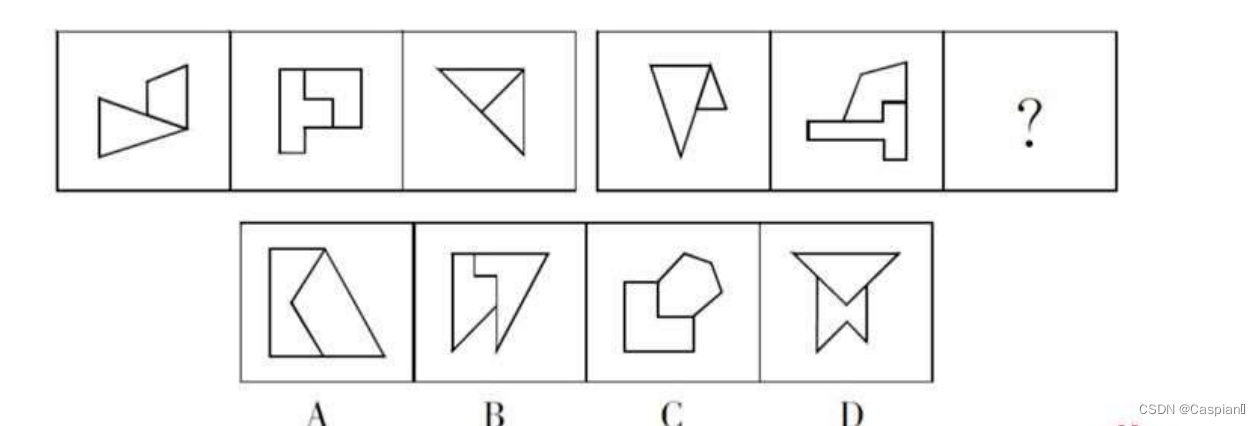
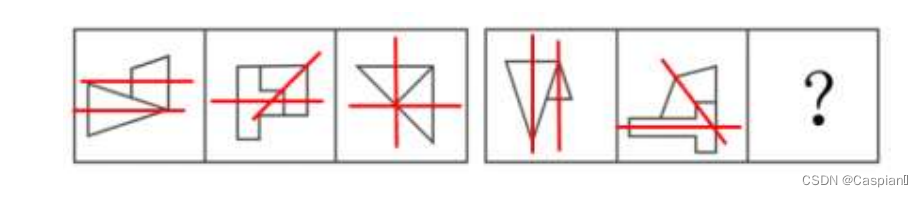
每个图形由两个小图形，这两个小图形对称轴夹角依次为180度、45度、90度，故选D。

 （2）

 

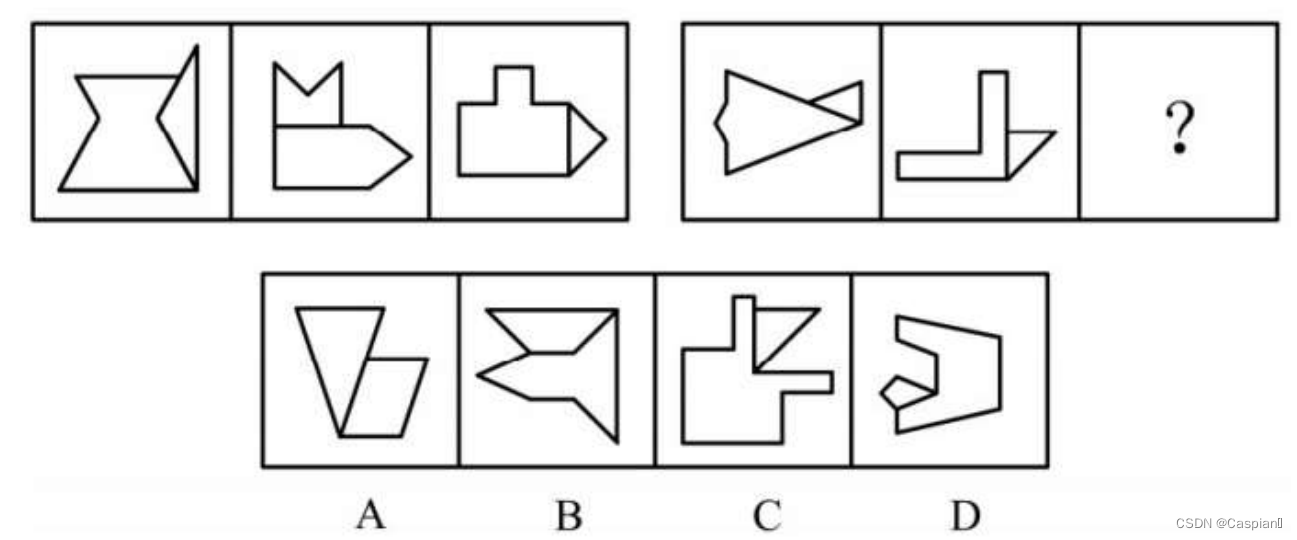
 第一组图形两个小图形对称轴夹角均为90度；第二组图形两个小图形夹角均为180度，故选D

4.对称轴与图形位置关系

（1）

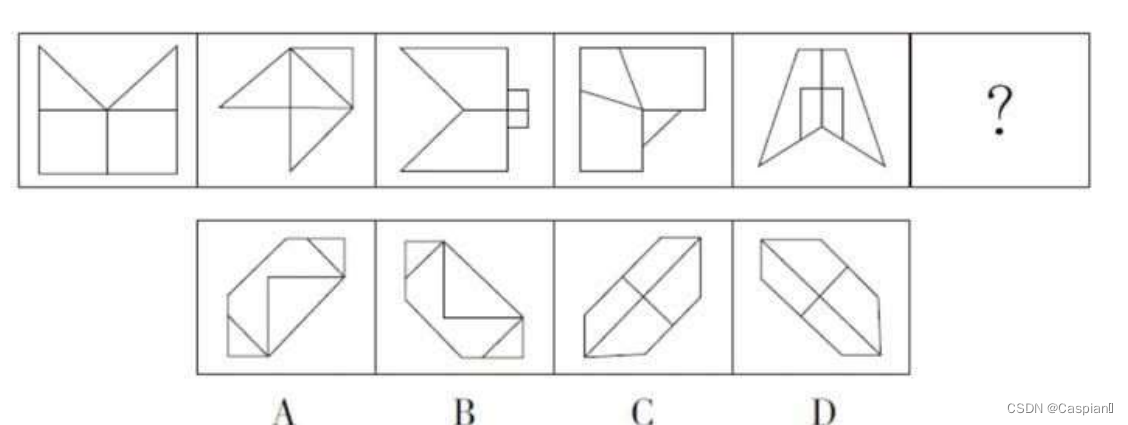
观察每个图形对称轴的方向，由对称轴的方向规律可以排除AC。再观察从第一个图形开始，对称轴与原图像的一条边重合、垂直、重合、垂直、重合，故选择无重合的B。

 （2）

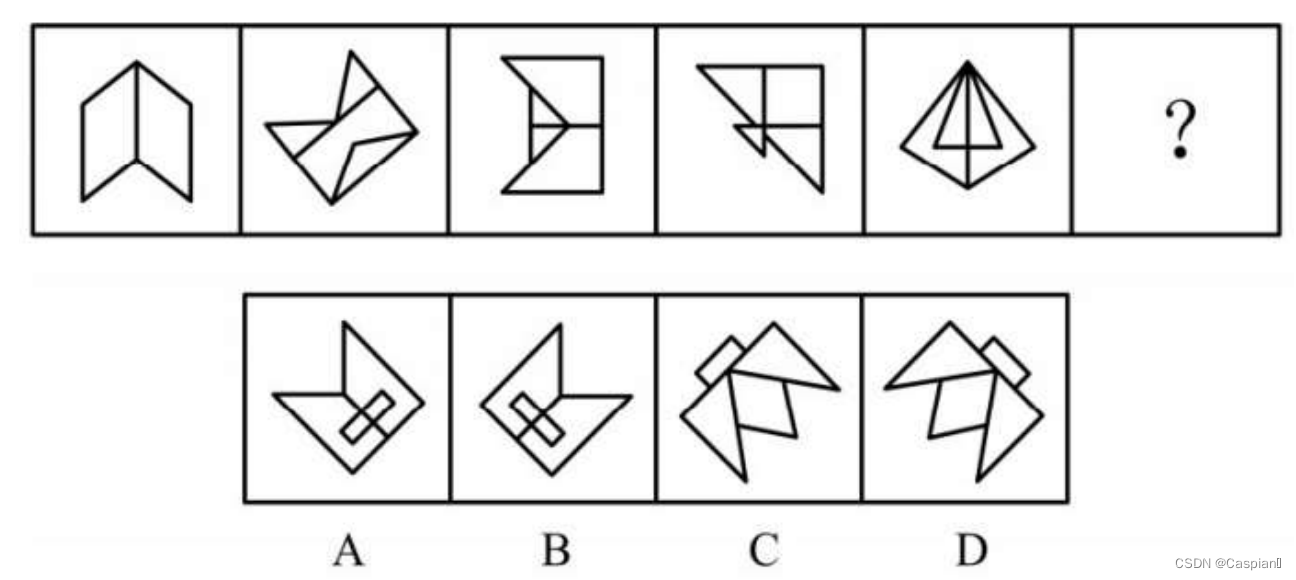
由对称轴方向规律锁定AC，再观察对称轴有无和原图像边重合的规律知答案选C。

（3）

 

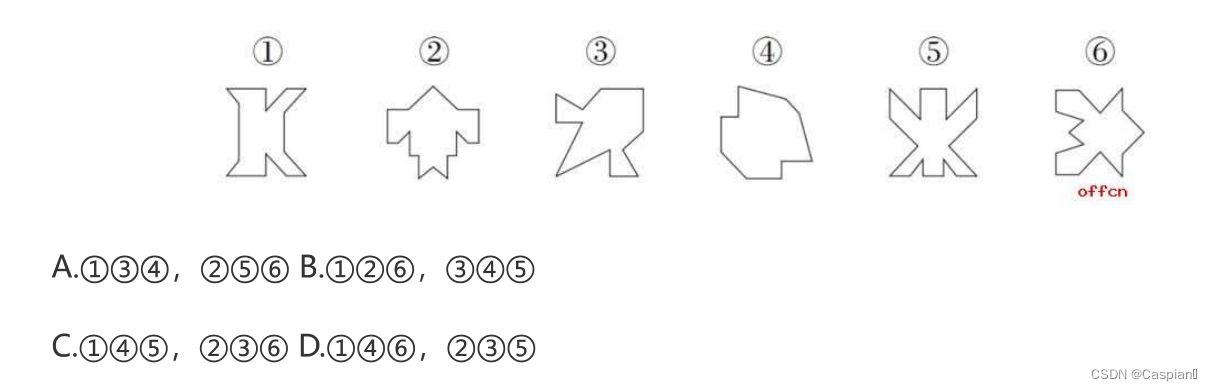
 1，4，5对称轴与原图像交于边；2，3，6对称轴与原图像交于点。