LeetCode-全排列（C++）

46. 全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

思路：本题使用回溯算法，如下图所示，第一层取1，剩余元素｛2，3｝，第二层在剩余元素里取2，剩下3，然后取3，得到第一个排列。

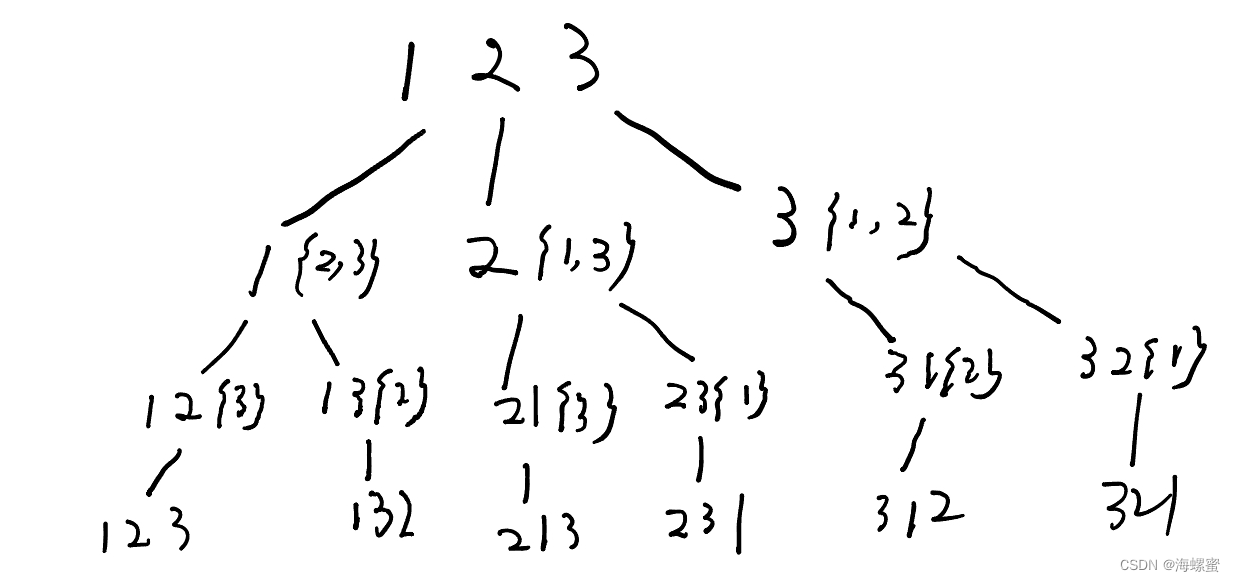
可以看出跟之前组合问题是不一样的，组合问题会用到startIndex标识起始位置，而排列问题是无法标识的，因为每一个元素都会被重复使用，所以每一层for循环横向遍历都是从0开始，到nums.size()-1结束。

这里要用到used数组，记录path里哪些元素被使用过了，在遍历时，跳过使用过的元素。

定义全局变量result为结果集，path为收集到的排序。for循环横向遍历，递归纵向遍历，把它想象成树状结构，收集叶子节点值。

回溯三部曲：

1. 确定回溯函数参数和返回值：回溯函数的参数有数组nums和标识path里元素是否被使用过的数组used。回溯函数的返回类型一般都会void类型。
2. 确定回溯函数的终止条件：如果path的大小等于nums的大小，说明搜索到了叶节点，return。
3. 确定单层搜索的过程：for循环横向遍历，递归过程纵向遍历，for循环每次从0开始遍历。如果当前元素值在used中出现过，跳过，继续下一个元素。否则，将当前元素值加入path，标识当前元素已经使用过，即used[i]=true，递归函数不断调用自己往深处遍历。然后递归函数下面要写回溯部分，撤掉本次处理的结果，path弹出最后一个值，used[i]=false。

代码：

class Solution {	//46. 全排列
public:
	vector<vector<int>> result;
	vector<int> path;
	void backtracking(vector<int> const& nums, vector<bool>& used) {
		if (path.size() == nums.size()) {
			result.push_back(path);
			return;
		}

		for (int i = 0; i < nums.size(); ++i) {
			if (used[i] == true) continue;
			used[i] = true;
			path.push_back(nums[i]);
			backtracking(nums, used);
			path.pop_back();
			used[i] = false;
		}
	}

	vector<vector<int>> permute(vector<int>& nums) {
		vector<bool> used(nums.size(), false);
		backtracking(nums, used);
		return result;
	}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

参考资料：代码随想录