前言

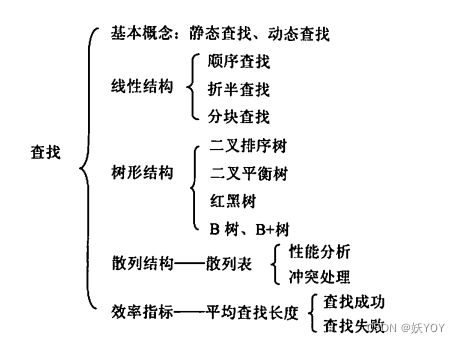
查找算法评价指标

• 查找长度——在查找运算中需要对比关键字的次数称为查找长度
• 平均查找长度（ALS）——所有查找过程中进行关键字的比较次数的平均值，有成功查找和失败下的查找长度

动态演示链接

对于哪个步骤不明白的可以在这里看下实际过程

顺序查找法

思想：从头到尾挨个找（反过来也行）
顺序查找时间复杂度：$O(n)$
代码：

#define MAXSIZE 100
typedef int ElemType;

typedef struct{				//查找表的数据结构(顺序表)
	ElemType *elem;			//动态数组基址
	int TableLen;			//表的长度
}SSTable;

//顺序查找
int Search_Seq(SSTable ST, ElemType key){
	int i;
	for(i=0; i<ST.TableLen && ST.elem[i] !=key; i++); 
	//查找成功,则返回元素下标;查找失败,则返回-1
	return i==ST.TableLen? -1 : i;
}

//“哨兵”
int Search_Seq_(SSTable ST, ElemType key){
	//数据从下标1开始存储 
	ST.elem[0]=key;		//“哨兵”
	int i;
	for(i=ST.TableLen; ST.elem[i]!=key; i--);		//从后往前找
	return i;		//查找成功,则返回元素下标;查找失败,则返回0
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

折半查找法

又称“二分查找”，仅适用于有序的顺序表
折半查找时间复杂度＝$O({\log }_{2}n)$
代码：

//结构体
typedef struct{
	ElemType *elem;
	int length;
}SSTable;

int Search_Bin(SSTable ST,ElemType key){
   // 在有序表ST中折半查找其关键字等于key的数据元素。
   // 若找到，则函数值为该元素在表中的位置，否则为-1。 
   int low=0,high=ST.length-1;							//置查找区间初值
   int  mid;
   while(low <= high){
	   mid = (low+high)/2;
      if(key==ST.elem[mid])
	  	return mid;      		//找到待查元素
      else if(key<ST.R[mid].key)
	  	high = mid -1;			//继续在前半部分查找
      else
	  	low = mid + 1;			//继续在后半部分查找
   }
   return -1;										//表中不存在待查元素
}// Search_Bin
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

分块查找法

思想：
索引表中记录每个分块的最大关键字、分块的区间；
先查索引表（顺序或折半），再对分块内进行顺序查找。
块内无序，块间有序

设索引查找和块内查找的平均查找长度分别为$L_1$、$L_s$,则分块查找的平均查找长度为$ASL=L_1+L_s$
$ALS=\frac{s^2+2s+n}{2s}，当s=\sqrt{n}时，AL{S}_{最小}=\sqrt{n}+1$

树形查找法

n个结点的二叉树最小高度为 $\lfloor {\log }_{2}n\rfloor +1$ 或是 $\lceil {\log }_2(n+1)\rceil$
对具有n个关键字的树型结构，具有n+1个叶结点

二叉排序树，BST

粘一下定义，简单的说就是，左子树节点值 $\le$ 根节点值 $\le$ 右子树结点值

[-] 查找思路：
若树非空，目标值与节点的值比较：
若相等，则查找成功；
若小于根节点，则在左子树上查找，否则在右子树上查找；
查找成功返回节点指针，失败返回NULL

下面是个完整的代码，包括构建二叉树，查找，删除和中序遍历：

#include<iostream>
using namespace std;


//结构体，二叉排序树节点
typedef struct BSTNode{
	int data;
	struct BSTNode *lchild, *rchild;
}BSTNode, *BSTree;

//二叉排序树中查找值为data的节点
//非递归，循环
BSTNode *BST_Search(BSTree T, int key){
	while(T != NULL && key != T->data){
	 	//若树空（未找到），或等于根节点值，则结束循环
		if(key < T->data) T = T->lchild;		//小于，在左子树上查找
		else T = T->rchild;			//大于，在右子树上查找
	}
	return T;
}

//递归查找 
BSTNode *SearchBST(BSTree T, int key){
	if(T == NULL) return NULL;	//查找失败
	if(key == T->data)	return T;	//查找成功
	else if (key < T->data)
		return SearchBST(T->lchild, key);		//在左子树查找
	else
		return SearchBST(T->rchild, key);		//在右子树查找
}


//插入 ，递归 
void InsertBST(BSTree &T,int e){
	if(T == NULL){                		//!T	//找到插入位置，叶子节点（或根） 
		BSTree S = new BSTNode;            //生成新结点S
		S->data = e;                  		//新结点S的关键字为e   
		S->lchild = S->rchild = NULL;		//新结点S作为叶子结点
		T = S;            					//把新结点S链接到已找到的插入位置
	}
	//这里不考虑相同的数字，有相同的数只算一个 
	else if (e< T->data) 
		InsertBST(T->lchild, e );			//将S插入左子树
	else if (e> T->data) 
		InsertBST(T->rchild, e);			//将S插入右子树
}// InsertBST 

void CreateBST(BSTree &T ) {
	//依次读入一个关键字为key的结点，将此结点插入二叉排序树T中
	T=NULL;
	int e;
	cout<<"请输入若干整数，用空格分开，以-1结束输入"<<endl;
	cin>>e;
	while(e != -1){			//-1，结束标志
	InsertBST(T, e);		//将此结点插入二叉排序树T中
	cin>>e;	
	}            
}//CreatBST

void DeleteBST(BSTree &T,int key) {
	//从二叉排序树T中删除关键字等于key的结点
	BSTree p=T;
	BSTree f=NULL;                     	//初始化
	BSTree q,s;
	
	while(p){
	//从根开始查找关键字等于key的结点*p           
	if (p->data == key) break;  	      	//找到关键字等于key的结点*p，结束循环
	f=p;                                		//*f为*p的双亲结点
	if(p->data> key)
		p=p->lchild;     	//在*p的左子树中继续查找
	else
		p=p->rchild;  	                  		//在*p的右子树中继续查找
	}//while
  
	if(!p) return;				//p==NULL	//找不到被删结点则返回
	
	/*―考虑三种情况实现p所指子树内部的处理：*p左右子树均不空、无右子树、无左子树―*/
	if((p->lchild) && (p->rchild)){     		//被删结点*p左右子树均不空
		q = p;
		s = p->lchild;
		while (s->rchild)                			//在*p的左子树中继续查找其前驱结点，即最右下结点
		{q = s; s = s->rchild;}	         		//向右到尽头
		p->data = s->data;               			//s指向被删结点的“前驱”
		if(q!=p){
		 q->rchild = s->lchild;     	//重接*q的右子树
		}
		else q->lchild = s->lchild;		//重接*q的左子树
		delete s;
	}else{
		if(!p->rchild){						//被删结点*p无右子树，只需重接其左子树
			q = p; p = p->lchild; 
		}
		else if(!p->lchild){               		//被删结点*p无左子树，只需重接其右子树
			q = p; p = p->rchild;
		}
		/*―――――将p所指的子树挂接到其双亲结点*f相应的位置―――――*/
		if(!f) T=p;                       			//被删结点为根结点
		else if (q==f->lchild) f->lchild = p;   	//挂接到*f的左子树位置
		else f->rchild = p;                 		//挂接到*f的右子树位置
		delete q;
	}
}//DeleteBST

//中序遍历
void InOrderTraverse(BSTree &T){
	if(T){
		InOrderTraverse(T->lchild);
		cout<<T->data<<" ";
		InOrderTraverse(T->rchild);
	}
}

int  main()
{
	BSTree T;
	CreateBST(T);		//相同的数只算一个 
	cout<<"当前有序二叉树中序遍历结果为："<<endl;
	InOrderTraverse(T);
	
	int key;//待查找或待删除内容
	cout<<"\n\n请输入待查找关键字（整数）："<<endl;
	cin>>key;
	BSTree result_1=BST_Search(T,key);	//循环查找 
	BSTree result_2=SearchBST(T,key);	//递归查找 
	if(result_1 && result_2)
		cout<<"循环和递归都，找到了关键字"<<key<<endl;
	else
		cout<<"未找到"<<key<<endl;
	
	cout<<"\n请输入待删除的关键字："<<endl;
	cin>>key;
	DeleteBST(T,key);
	cout<<"当前有序二叉树中序遍历结果为（删除后）："<<endl;
	InOrderTraverse(T);
    return 1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137

平衡二叉排序树，AVL

AVL Tree链接
$|左子树高-右子树高|\le 1$，平衡因子只可取-1、0或1。

插入，四种情况
1）LL，右单旋转

2）RR，左单旋转

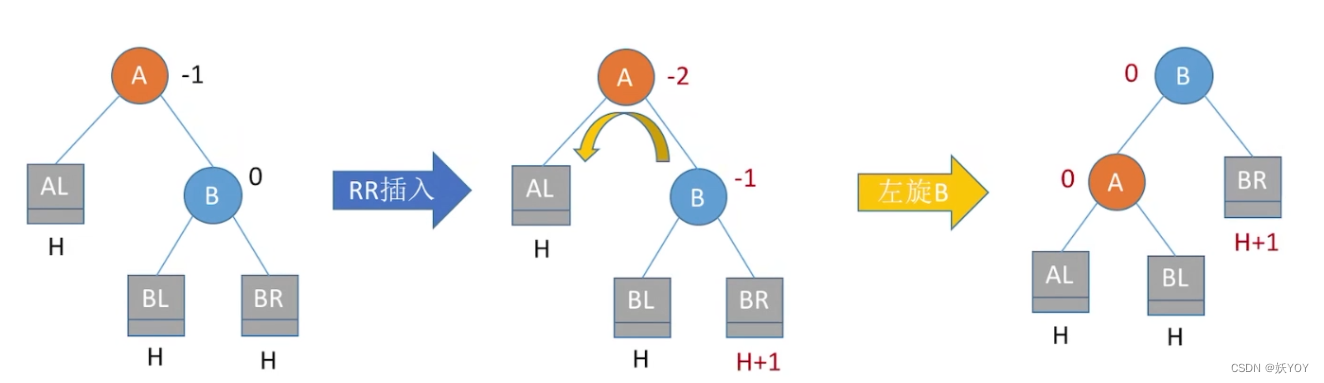
3）LR，左旋，右旋

4）RL，右旋，左旋

删除，步骤：
①删除节点（方法同，二叉排序树）

• 若删除的节点是叶子，直接删；
• 若删除的节点只有一个子树，用子树顶替删除位置；
• 若删除的节点有两棵子树，用前驱（或后继）结点顶替，并转化未对前驱（或后继）结点的删除。

②一路向上找到最小不平衡子树，找不到就over
③找最小不平衡子树下，”个头“最高的儿子，孙子
④根据孙子的位置，调整平衡（LL/RR/LR/RL）

• 孙子在LL：儿子右单旋；
• 孙子在RR：儿子左单旋；
• 孙子在LR：孙子先左旋，再右旋；
• 孙子再RL：孙子先右旋，再左旋；

⑤如果不平衡向上传导，继续②

红黑树，RBT

Red/Black Tree链接

为什么要发明 红黑树：

简要特点：
左右跟，根叶黑
不红红，黑路同

详细特点：
左子树结点值 $\le$ 根结点值 $\le$ 右子树结点值
①每个结点或是红色,或是黑色的；
②根节点是黑色的；
③叶结点(外部结点、NULL结点、失败结点)均是黑色的；
④不存在两个相邻的红结点(即红结点的父节点和孩子结点均是黑色)；
⑤对每个结点,从该节点到任一叶结点的简单路径上,所含黑结点的数目相同；

插入，这张图xswl

• 黑叔

• 红叔
  

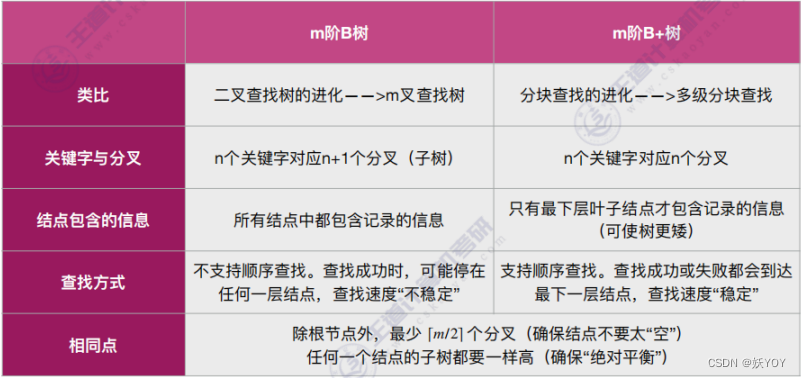
B树

B-Tree 链接

---

令$k=\lceil m/2\rceil$
$高度为h的m阶B树，含有关键字个数至少是：2\cdot k^{h-1}-1$
$$1+2(k-1)(k^0+k^1+\cdots +k^{h-2})=1+2(k^{h-1}-1)=2\cdot k^{h-1}-1$$
高度为h的3阶B树，含有关键字个数至少是：$2^h-1$，同完全二叉树（满二叉）
高度为h的5阶B树，含有关键字个数至少是：$2\cdot 3^{h-1}-1$

高度为h的完全二叉树至少$2^{h-1}$个结点，最多$2^h-1$个结点

---

下面说明下B树特征和形状，先来个5叉树，B树就是在多叉树加一些约束，

B树结构：

对于高度问题，

---

对于插入，看不懂跳过：

插入和删除：

B+树

• B+树有点像是分块查找结构和B树的整合，只在叶子结点存信息，非叶结点仅（上面的）起索引作用，查找也是找到最下层；
• B+树支持顺序查找和随机查找，叶子结点本身依关键字从小到大顺序链接
• 根据B+树的特征，在操作系统中用的挺多，从磁盘里读数据到内存、关系型数据库的“索引”（如MySQL）。

散列表（哈希表）

还是用图片粘上吧：

装填因子$\alpha$越大，平均查找长度变大，“冲突”越多，查找效率越低

常见的散列函数

1. 直接定址法，$H(key)=key或H(key)=a\times key+b$
2. 除留余数法，$H(key)=key\%p$，p取不大于散列表长度m但最接近或等于m的质数
3. 数字分析法，设关键字是r进制数(如十进制数) ，而r个数码在各位上出现的频率不一定相同，可能在某些位上分布均匀一些，每种数码出现的机会均等；而在某些位上分布不均匀，只有某几种数码经常出现，此时可选取数码分布较为均匀的若干位作为散列地址。这种方法适合于已知的关键字集合，若更换了关键字，则需要重新构造新的散列函数。例：手机号后四位
4. 平方取中法，这种方法得到的散列地址与关键字的每位都有关系，得到的散列地址分布比较均匀，适用于关键字的每位取值都不够均匀或均小于三别地址所需的位数

处理冲突方法

• 拉链法，下图：
  
• 开放定址法，下图：
  

  • ①线性探测法：$d_i=0,1,2,3,\cdots ,m-1$，即发生冲突时,每次往后探测相邻的下一个单元是否为空。线性探测法很容易造成同义词、非同义词的“聚集(堆积)”现象，严重影响查找效率产生原因——冲突后再探测一定是放在某个连续的位置。
    查找效率分析：
    

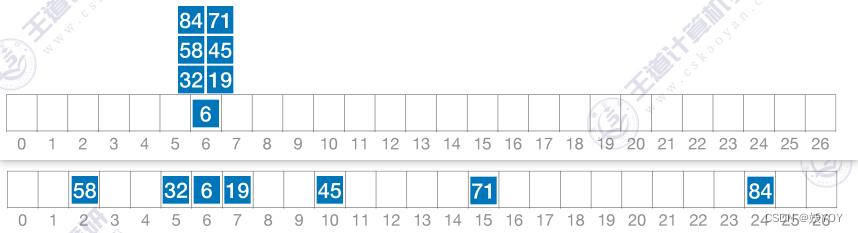
  • ②平方探测法，当$d_i=0^2,1^2,-1^2,2^2,-2^2,\cdots ,k^2,-k^2$时,称为平方探测法,又称二次探测法,其中$k\le m/2$。比起线性探测法更不容易产生“聚集（堆积）”问题。
    

  • ③伪随机序列法，$d_i$是一个伪随机序列，自己定义的，如$di=0,3,5,11,\dots$

  • ④再散列法（再哈希法）：除了原始的散列函数$H(key)$之外，多准备几个散列函数，当散列函数冲突时，用下一个散列函数计算一个新地址，直到不冲突为止。