数据结构之排序

基础知识铺垫

比较排序与非比较排序

• 比较类排序：通过比较来决定元素间的相对次序，由于其时间复杂度不能突破O(nlogn)，因此也称为非线性时间比较类排序。比如：冒泡排序，归并排序，快速排序，插入排序，选择排序，希尔排序，堆排序等
• 非比较类排序：不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。 比如：基数排序，计数排序，桶排序

内排序主要放在内存中，外排序，排序的记录个数太多，不能同时放在内存，整个排序过程要在内外存之间多次交换数据。

高效率的排序算法应该具有尽可能少的关键字比较次数，尽可能少的记录移动次数

稳定性：

• 稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面。
• 不稳定：如果a原本在b的前面，而a=b，排序之后 a 可能会出现在 b 的后面。

各种排序的分类 时间复杂度，空间复杂度，及稳定性的分析

---

冒泡排序

如果相邻元素的顺序错误，它会重复交换相邻元素。该算法不适用于大型数据集，因为它的平均和最坏情况时间复杂度非常高。

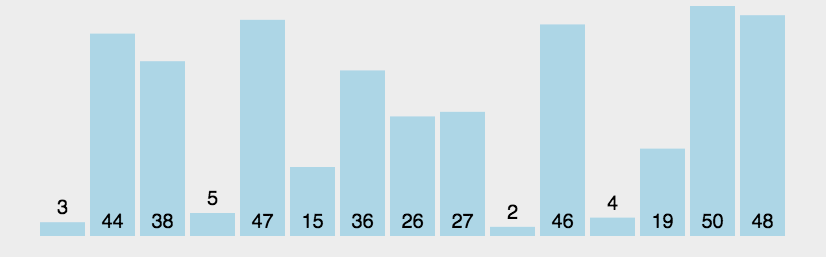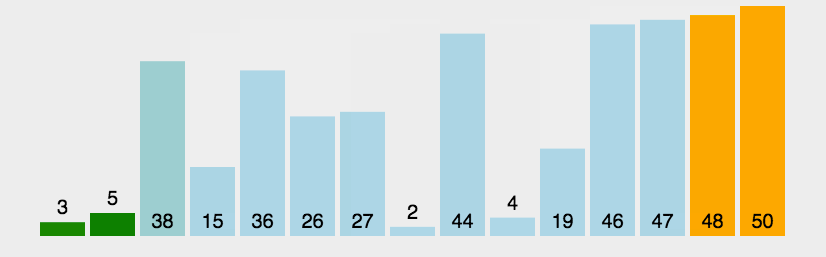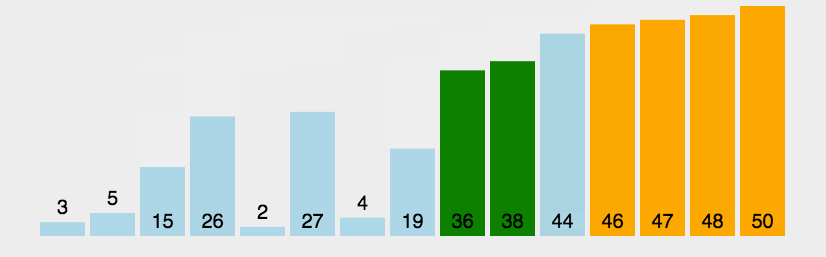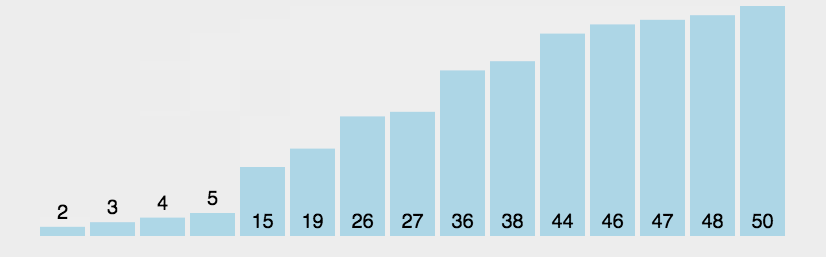
冒泡排序主要思想：

1.从第一对开始相邻元素两两进行比较，按照升序来看，前面的元素大于后面的元素就进行交换,第一趟排序之后将最大的元素到达到最后的位置

2.第一趟排序结束后，最大的元素已经排好序不需要动了之后的排序也就不需要移动它，随着每一趟交换次数减少，就趋近于有序。

3.总共要排序n-1趟(比如10个元素要进行9趟排序)，每一趟也依据趟数的增加，交换次数也减少，内层循环每一趟排序，已经排好序的不需要再排序，所以循环次数为n-1-i

主要代码实现：

import java.util.*;
class TestDemo{
    public static void bubbleSort(int[] array){
          for(int i =0;i<array.length-1;++i){
                for(int j =0;j<array.length-1-i;++j){
                      if(array[j]>array[j+1]){
                             int tmp = array[j];
                             array[j] = array[j+1];
                             array[j+1] = tmp;
                      }
                }
          }
    }
    
    public static void main(String[] args){
     int[] array = {9,8,6,5,7,4,3,2,1,0,2,5,6,22,5,56,5};
     bubbleSort(array);
     System.out.println(Arrays.toString(array));
    }
}

冒泡排序的优化实现：

冒泡排序有可能某一趟已经是有序的(比如:132456789,从4以后在没有排序之前就是有序的)，那就不需要在进行排序也就减少了循环次数。

优化冒泡排序代码实现：

import java.util.*;
class TestDemo{
    public static void bubbleSort(int[] array){
          for(int i =0;i<array.length-1;++i){
              boolean flag = false;
                for(int j =0;j<array.length-1-i;++j){
                      if(array[j]>array[j+1]){
                             int tmp = array[j];
                             array[j] = array[j+1];
                             array[j+1] = tmp;
                      }
                      flag = true;
                }
              if(!flag){
                  break;
              }
          }
    }
   
    public static void main(String[] args){
     int[] array = {9,8,6,5,7,4,3,2,1,0,2,5,6,22,5,56,5};
     bubbleSort(array);
     System.out.println(Arrays.toString(array));
    }
}

冒泡排序的最好情况和最坏情况的分析

冒泡排序的最好情况就是在没有排序之前就已经是排好序的(比如要求按照升序排列，没排序之前已经是升序排列)，这个时间复杂度就是O(N)。

冒泡排序的最坏情况：与要求正好是相反的顺序(比如要求是升序，但没排序之前是降序)，时间复杂度为O(N^2)

在第 1 阶段：比较次数 = (n-1)
交换次数 = (n-1)

在第 2 阶段：比较次数 = (n-2)
交换次数 = (n-2)

在第 3 阶段：比较次数 = (n-3)
交换次数 = (n-3)
. . . . . . . .
. . . . . . . .
在通过 n-1 时：比较次数 = 1
交换次数 = 1

现在，计算排序数组所需的比较总数
= (n-1) + (n-2) + (n-3) + 。. . 2 + 1
= (n-1)*(n-1+1)/2 { 通过使用 N 个自然数之和公式 }
= n (n-1)/2

对于最坏的情况：

交换总数 = 比较总数 比较
总数（最坏情况）= n(n-1)/2
交换总数（最坏情况）= n(n-1)/2

最坏和平均案例时间复杂度： O(N 2 )。最坏的情况发生在对数组进行反向排序时。

最佳案例时间复杂度： O(N)。最好的情况发生在数组已经排序时。

辅助空间(空间复杂度)： O(1)---->原地算法（冒泡排序是一种就地算法）

冒泡排序的边界：在使用冒泡排序的时候要是事先检查是否是已经排好序的避免时间复杂度为O(n^2)

冒泡排序是稳定的排序:在进行交换时候只交换不相等的元素。

---

选择排序

选择排序思想：

选择排序算法通过从未排序的部分重复找到最小元素（考虑升序）并将其放在开头来对数组进行排序。该算法在给定数组中维护两个子数组。

• 已经排序的子数组。
• 剩余未排序的子数组。

在选择排序的每次迭代中，未排序的子数组中的最小元素（考虑升序）被挑选出来并移动到已排序的子数组中。

交换移动数据次数较少

选择排序主要是最开始将第一个元素看做是有序的，然后从第一个元素后面未排序的数字中挑选出最小的与第一个元素交换，然后在将前两个看做是有序的，在第二个元素后面寻找一个次小的数字与第二个数字进行交换.....以此类推，也就是维护两个子数组，一个是排好序的子数组，一个是未排序的子数组，然后将未排序的子数组的元素移动到已经排好序的子数组中，最后整体有序。

---

代码实现：

    //选择排序
    public static void selectSort(int[] array){
        for(int i =0;i<array.length;++i){
            int minIndex = i;
            for(int j=i+1;j<array.length;++j){
                if(array[j]<array[minIndex]){
                    minIndex = j;
                }
            }
            swap(array,i,minIndex);
        }
    }

选择排序时间复杂度：

选择排序是选择一个元素(一个for循环)，然后在这个元素后面找最小值(一个for循环) 在进行交换，所以时间复杂度是O(N^2).

选择排序空间复杂度：

O(1) 作为唯一使用的额外内存用于临时变量，同时交换 Array 中的两个值。选择排序的好处是它永远不会超过 O(n) 交换，并且在内存写入是一项昂贵的操作时很有用。

选择排序稳定性

选择排序默认是不稳定的

插入排序

插入排序动图

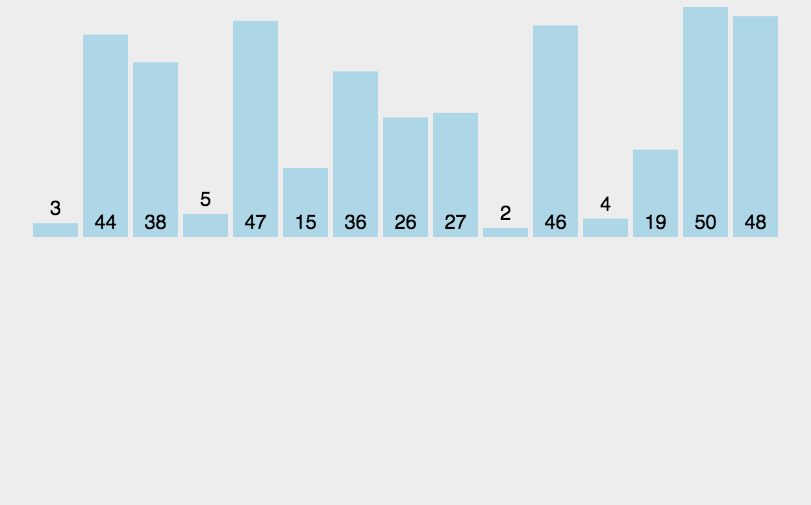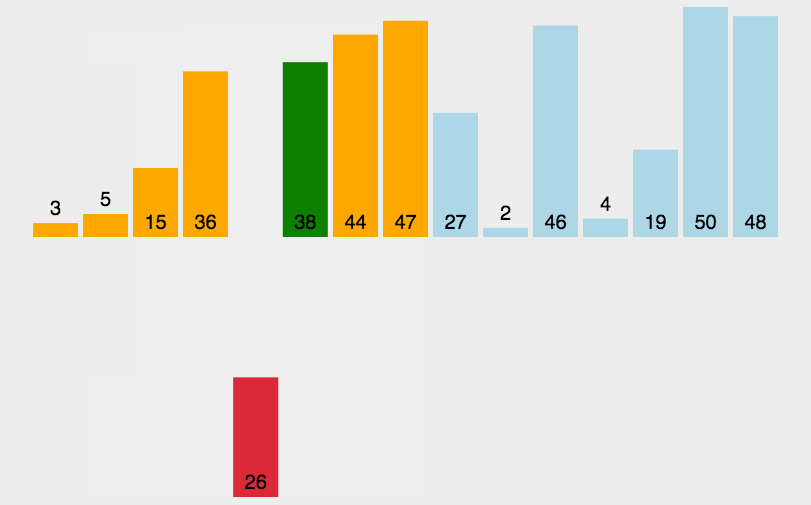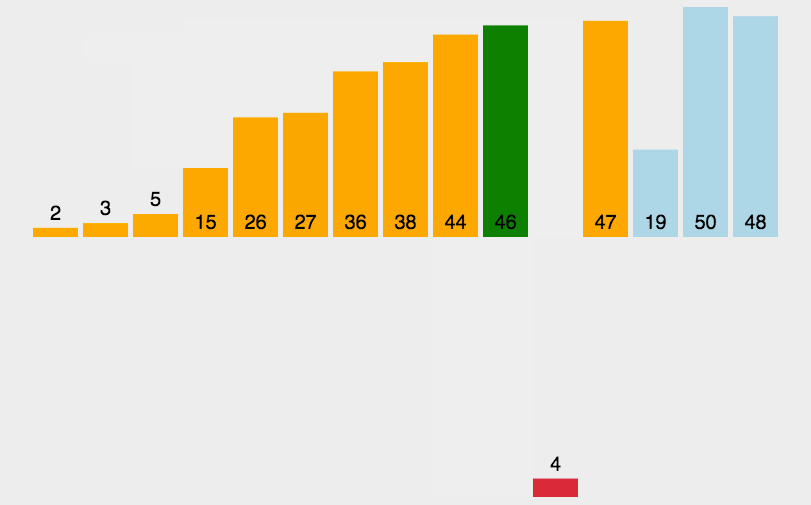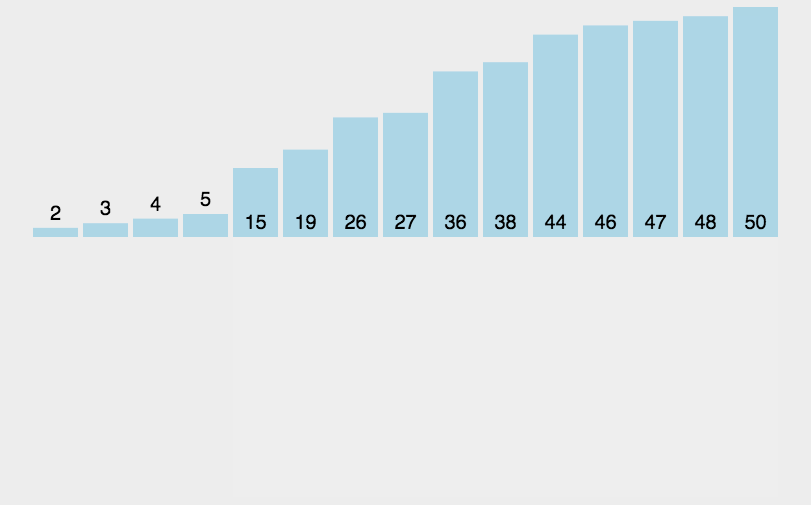
插入排序思想：

插入排序分为有序子数组和语序子数组，我们将无序子数组中的元素一一插入到有序子数组当中，最终整个数组就是有序的。(最开始将下标1前面的元素看做是有序的(不包括1本身)，然后将1下标的元素插入到前面让数组变得有序，那么当插入完成之后下标0,1就都是有序的，接着2,3.....,最终数组就是有序的)。

代码实现：

    //插入排序
    public static void insertSort(int[] array){
        for(int i =1;i<array.length;++i){
            int tmp = array[i];
            int j =i-1;
            for(;j>=0;j--){
                if(array[j]>tmp){
                    array[j+1] = array[j];
                }else {
                    break;
                }
            }
            array[j+1] = tmp;
        }
    }

插入排序时间复杂度、空间复杂度、稳定性

时间复杂度：当情况好的时候也就是数组本身就是与预期排序一样，本身就有序，只进行n-1次比较不进行移动元素，时间复杂度是O(N)

当情况不好的时候也就是与预期排序相反比如你要的是升序，而数组本身是降序的，比较次数突然升到n^2次数，交换次数也是要交换n^2次。

空间复杂度：需要借助O(1)的辅助空间来临时保存待插入元素，空间复杂度是O(1)

稳定性：由于array[j]>tmp这个条件，移动元素时候没有=，插入排序是一个稳定的排序

插入排序适用情况：当数据量趋近于有序，或者少量的插入元素是直接插入排序更加的高效，比如适合快速排序数据量较小时可以使用直接插入排序进行优化，是快速排序算法更加快，优秀。

参考文献：

---

希尔排序

希尔排序思想：

希尔排序是对直接插入排序的改进，如果插入排序数据量较大并且是逆序的不好情况就会很慢，时间复杂度为O(n^2),而希尔排序将其数组分成若干子数组，让子数组有序，整个数组就基本趋近于有序(这个基本有序并不是真正的有序，而是让小的数组进本都在前面，大的数字基本都在后面，不大不小的数字都在中间)，希尔排序又叫做缩小增量排序，原来直接插入排序是间隔为1的进行插入，希尔排序是间隔为gap的进行插入，gap每一次都在缩小，使得数组基本有序，但最终一定要再进行一次直接插入排序，这样数组就是有序的。

代码实现：

    //希尔排序
    public static void shellSort(int[] array){
        int gap = array.length;
        while(gap>1){
            gap=gap/3+1;
            for(int i =gap;i<array.length;++i){
                int tmp = array[i];
                int j =i-gap;
                for(;j>=0;j-=gap){
                    if(array[j]>tmp){
                        array[j+gap] = array[j];
                    }else {
                        break;
                    }
                }
                array[j+gap] = tmp;
            }
        }
    }

希尔排序时间复杂度、空间复杂度、稳定性分析

时间复杂度：O(n^1.5)~O(n^1.7)

空间复杂度：与插入排序一样利用了O(1)的辅助空间来临时存储元素，时间复杂度为O(1)，就地排序

稳定性：希尔排序由于增量一直在改变，是跳跃式的移动，所以是希尔排序是一个不稳定的排序。

---

堆排序

堆排序思想：

堆排序主要是建堆(从小到大排序建大堆，从大到小排序建小堆)和向下调整，由于我们建立大堆，堆顶元素是最大的，我们将其堆顶元素与数组最后一个有效元素进行交换，当交换之后最后的一个元素已经是有序的，然后每交换一次元素都要调整为大堆，反复执行最终就是有序的。

代码实现：

//建堆
public void createHeap(int[] array){
    //将array数组元素都保存到elem数组中去
    for(int i =0;i<array.length;++i){
        this.elem[i] = array[i];
        this.usedSize++;
    }
    //上面那段代码只是拷贝数组不能算做建堆中
    //通过找到最后一个父节点来进行向下调整
    for(int p = (this.usedSize-1-1)/2;p>=0;p--){
        shiftDown(this.elem,p,this.usedSize);
    }
}

//向下调整算法
public void shiftDown(int[] array,int parent,int len){
    int child = 2*parent+1;
    while(child<len){
        //找左右孩子节点最大的值
        if(child+1<len&&array[child]<array[child+1]){
            child++;
        }
        //此时child就是左右孩子节点最大的
        //与父亲节点进行比较
        if(array[parent]<array[child]){
            swap(array,parent,child);
        }else {
            break;//并不需要进行交换这棵树已经是大根堆
        }
        parent = child;
        child = 2*parent+1;
    }
}
//堆排序
public void heapSort(int[] array){
    //从小到大排序需要建大堆
    int end = array.length-1;
    while(end>0){
        swap(array,0,end);
        shiftDown(array,0,end);
        end--;
    }
}

堆排序时间复杂度、空间复杂度、稳定性分析

时间复杂度：堆排序建堆是O(N),每一次向下调整需要调整高度log2(N),要将对堆顶做n-1次交换，所以时间复杂度是O(N+N*log2N) ===》O(N*log2N)

空间复杂度：没有利用额外的辅助空间空间复杂度为O(1)

稳定性：比较和交换是跳跃式的，是一个不稳定的排序

---

快速排序

快速排序相当于二叉树的前序遍历，先去寻找基准位置，将基准元素放到里面，然后划分为左右区间递归左区间和有区间，最终整体就是变得有序，快速排序的关键就是Partition函数，它会将基准元素放到数组他应该所处的位置，然后通过递归将所有元素都放到自己应该所处的位置，最终就变得有序了。

快速排序的关键partition函数

前后指针动图：

前后指针算法思想：

• Partition：定义两个指针prev,cur, 选取左边作为基准元素，cur负责在前面找比基准元素小的同时cur也会跳过比基准元素大的，所以prev和cur之间就是比基准元素大的，cur找到小，就++prev在交换，就把比基准元素大的放在后边，小的放在了前面。最终prev的位置就是基准元素的位置，将prev的位置与基准元素交换。
• 根据Paratition函数来划分出左边区间和右边区间，然后进行递归---->相当于二叉树的前序遍历(根-左-右)

代码实现：

//前后指针法
public static int partition3(int[] array,int left,int right){
    int pivot = left;
    int prev = left;
    int cur = left+1;
    while(cur<=right){
        //cur主要是找小，然后++prev就是大的元素在交换
        if(array[cur]<array[pivot]&&++prev!=cur){
            swap(array,cur,prev);
        }
        ++cur;
    }
    swap(array,prev,pivot);
    return prev;
}

hoare法动图：

hoare算法思想：

选取左边为基准元素，右边开始找比基准元素小的停下来，左边再开始找比基准元素大的停下俩，两者在进行交换，当两指针相遇则停下来，相遇位置就是基准元素应该所处的位置，将其与基准元素交换，此时基准元素前面的都比它小，后面的都比它大，为我们划分出左右区间然后在递归左边，和右边，最终有序

    //hoare法
    public static int partition2(int[] array,int left,int right){
        int pivot = left;
        while(left<right){
            //右边找小
            while(left<right&&array[right]>=array[pivot]){
                right--;
            }
            //左边找大
            while(left<right&&array[left]<=array[pivot]){
                left++;
            }
            swap(array,left,right);
        }
        //此时两者相遇，更新基准元素位置
        swap(array,left,pivot);
        return left;
    }

挖坑法动图：

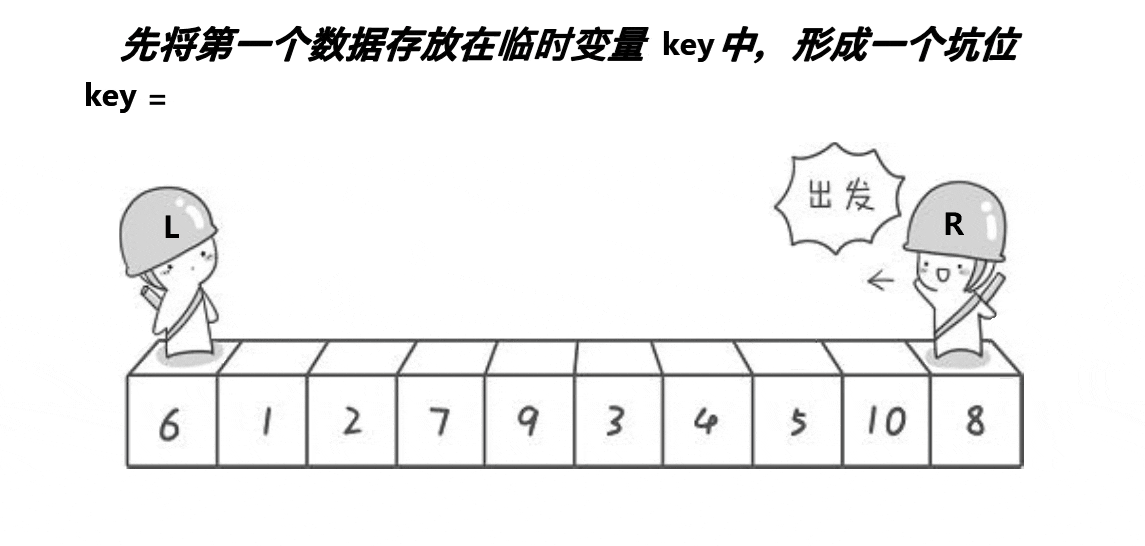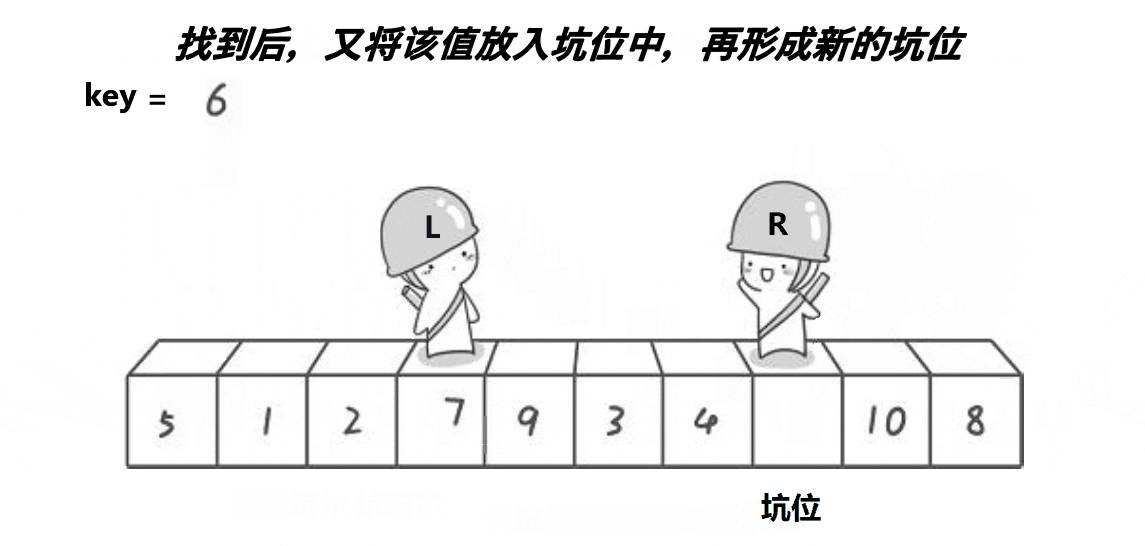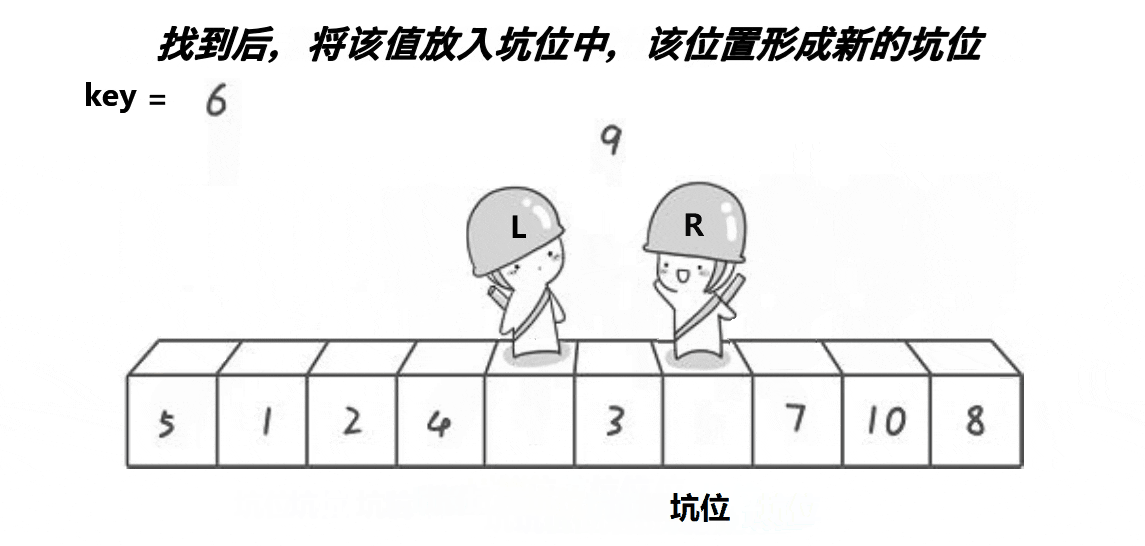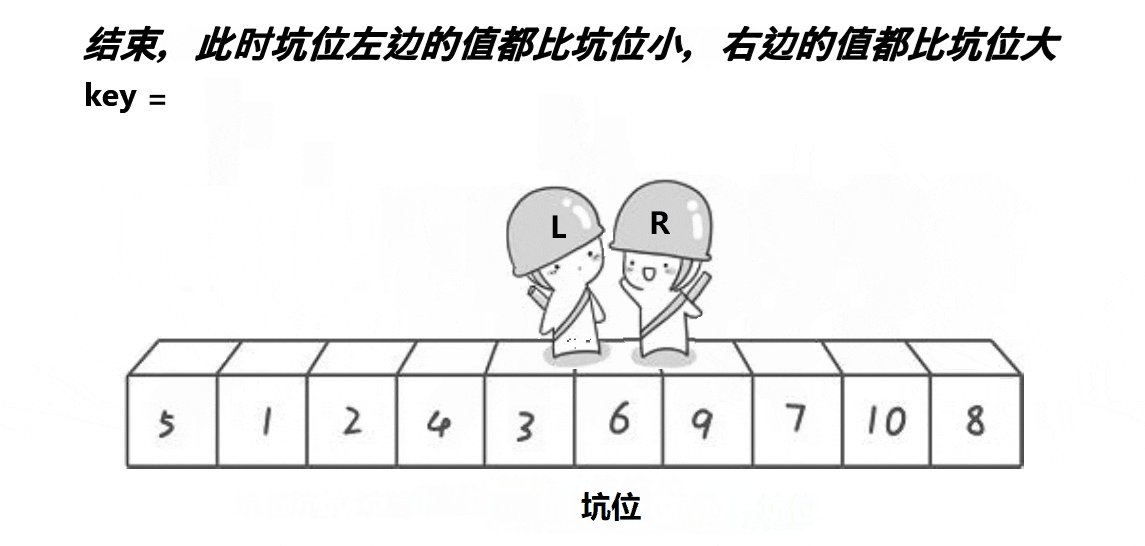
挖坑法思想：

• 选取左边元素作为基准元素保存起来，然后定义两个指针，左边作为基准元素相当于挖坑位，右边指针开始寻找比基准元素小的填上坑，也相当于在右边指针位置挖坑，同时左边指针也往后走寻找比基准元素大的填坑，重复执行后，左右指针相遇的位置就是基准元素应该所处的位置，然后将基准元素放到这个位置上面，从而这个相遇位置也给我们划分了左边区间和右边区间进行递归，最终就是有序的。

    //挖坑法
    public static int partition1(int[] array,int left,int right){
        int pivot =array[left];
        while(left<right){
            //左边挖坑右边埋坑-->右边找小
            while(left<right&&array[right]>=pivot){
                right--;
            }
            array[left] = array[right];
            //右边挖坑左边埋坑-->左边找大
            while(left<right&&array[left]<=pivot){
                left++;
            }
            array[right] = array[left];
        }
        array[left] = pivot;
        return left;
    }

快速排序的整体实现

上面的只是快速排序的核心函数，下面是快速排序的整体实现

代码实现：

    public static void quickSort(int[] array,int left,int right){
        if(left>=right) return ;
        int mid = partition3(array,left,right);
        quickSort(array,left,mid-1);
        quickSort(array,mid+1,right);
    }
    
    //for Test

    public static void main(String[] args) {
        int[] array = {27,15,19,18,28,34,65,49,25,37};
        //快速排序
        quickSort(array,0,array.length-1);
        System.out.println(Arrays.toString(array));
    }

快速排序的优化

直接插入排序优化

快速排序好的情况时间复杂度是O(n*log2N),而快速排序最坏的情况能到达O(N^2),最坏的情况也就是数据量区域有序的情况，而直接插入排序在数据量较小时，趋近于有序时候，直接插入排序更加的高效，所以我们可以，当快速排序数据量较小的时候，不要继续采用快速排序，而是直接采用直接插入排序。

public static void InsertSortToQuick(int[] array,int left,int right){
        for(int i = left;i<=right;++i){
            int tmp = array[i];
            int j = i-1;
            for(;j>=0;j--){
                if(array[j]>tmp){
                    array[j+1] = array[j];
                }else {
                    break;
                }
            }
            array[j+1] = tmp;
        }
    }
    public static void quickSort(int[] array,int left,int right){
        if(left>=right) return ;
        //插入排序优化
        if((left-right+1)<=5){
            InsertSortToQuick(array,left,right);
            return;
        }
        int mid = partition3(array,left,right);
        quickSort(array,left,mid-1);
        quickSort(array,mid+1,right);
    }

三数取中法优化

当数据量有序时候，不管是升序还是降序，快速排序的时间复杂度都是O(N^2),也就是一颗单分支的二叉树(有可能是往左边斜的树，有可能是往右边斜的树)，这样就是最坏的情况，我们选取的基准元素都是比后边元素大的或者都比后边元素小，这样有一个指针就会不动，复杂度就会特别高，那么有没有一种方法可以使得我们基准元素是不大不小的么？我们还可以采用三数取中法，就是在左边界，右边界，中间位置，选取中间大小的数字当做基准元素。

代码实现：

    public static int MiddleOfThree(int[] array,int left,int right){
        int mid = left+((right-left)>>>1);
        if(array[left]<array[right]){
            if(array[mid]>array[left]){
                return mid ;
            }else if(array[mid]>array[right]){
                return right;
            }else {
                return left;
            }
        }else {
            //left right
            if(array[mid]>array[left]){
                return left;
            }else if(array[mid]>array[right]){
                return right;
            }else {
                return mid;
            }
        }
    }

结合优化快速排序最终代码

  //挖坑法
    public static int partition1(int[] array,int left,int right){
        int pivot =array[left];
        while(left<right){
            //左边挖坑右边埋坑-->右边找小
            while(left<right&&array[right]>=pivot){
                right--;
            }
            array[left] = array[right];
            //右边挖坑左边埋坑-->左边找大
            while(left<right&&array[left]<=pivot){
                left++;
            }
            array[right] = array[left];
        }
        array[left] = pivot;
        return left;
    }

    //hoare法
    public static int partition2(int[] array,int left,int right){
        int pivot = left;
        while(left<right){
            //右边找小
            while(left<right&&array[right]>=array[pivot]){
                right--;
            }
            //左边找大
            while(left<right&&array[left]<=array[pivot]){
                left++;
            }
            swap(array,left,right);
        }
        //此时两者相遇，更新基准元素位置
        swap(array,left,pivot);
        return left;
    }

    //前后指针法
    public static int partition3(int[] array,int left,int right){
        int pivot = left;
        int prev = left;
        int cur = left+1;
        while(cur<=right){
            //cur主要是找小，然后++prev就是大的元素在交换
            if(array[cur]<array[pivot]&&++prev!=cur){
                swap(array,cur,prev);
            }
            ++cur;
        }
        swap(array,prev,pivot);
        return prev;
    }
    
    public static int MiddleOfThree(int[] array,int left,int right){
        int mid = left+((right-left)>>>1);
        if(array[left]<array[right]){
            if(array[mid]>array[left]){
                return mid ;
            }else if(array[mid]>array[right]){
                return right;
            }else {
                return left;
            }
        }else {
            //left right
            if(array[mid]>array[left]){
                return left;
            }else if(array[mid]>array[right]){
                return right;
            }else {
                return mid;
            }
        }
    }
    
    public static void InsertSortToQuick(int[] array,int left,int right){
        for(int i = left;i<=right;++i){
            int tmp = array[i];
            int j = i-1;
            for(;j>=0;j--){
                if(array[j]>tmp){
                    array[j+1] = array[j];
                }else {
                    break;
                }
            }
            array[j+1] = tmp;
        }
    }
    public static void quickSort(int[] array,int left,int right){
        if(left>=right) return ;
        //插入排序优化
        if((left-right+1)<=5){
            InsertSortToQuick(array,left,right);
            return;
        }
        //三数取中优化
        int index = MiddleOfThree(array,left,right);
        swap(array,left,index);
        int mid = partition3(array,left,right);
        quickSort(array,left,mid-1);
        quickSort(array,mid+1,right);
    }

    //for Test

    public static void main(String[] args) {
        int[] array = {27,15,19,18,28,34,65,49,25,37};
        
        //快速排序
        quickSort(array,0,array.length-1);
        System.out.println(Arrays.toString(array));
    }

快速排序非递归实现

快速排序非递归版本是利用栈来模拟递归过程每一次将递归的左右区间入栈，然后出栈，对左右进行Partition函数操作对齐进行划分，然后继续入栈左右两段区间到栈为空时，划分完毕。

//非递归法
    public static void partitionNor(int[] array,int left,int right){
          Stack<Integer> stack = new Stack<>();
          int mid = partition3(array,left,right);
          if(left<mid-1){
              stack.push(left);
              stack.push(mid-1);
          }
          if(right>mid+1) {
              stack.push(mid+1);
              stack.push(right);
          }
          while(!stack.isEmpty()){
              right = stack.pop();
              left = stack.pop();
              mid = partition3(array,left,right);
              if(left<mid-1){
                  stack.push(left);
                  stack.push(mid-1);
              }
              if(right>mid+1) {
                  stack.push(mid+1);
                  stack.push(right);
              }
          }
    }

快速排序时间复杂度、空间复杂度、稳定性分析

时间复杂度：好的情况下，递归深度(也就是树的高度)，每一次都要对N个元素进行划分所以时间复杂度为O(N*logN) 坏的情况下，也就是一颗单分支的树，一颗往左斜的树或者往右斜的树，每次再划分时都有一个指针不动，另一个指针遍历整个数组，所以时间复杂度是O(N^2)(所以为了解决这个问题就有了快速排序的优化)

空间复杂度：O(logN) ~ O(N)（正产情况下递归深度也就是树的高度为O(logN）不好的情况下树的高度就是数组总元素个数，所以不好的情况空间复杂度为O(N)）

稳定性分析：不稳定(在进行Partition函数的时候有跳跃式的移动所以是不稳定的排序)

归并排序动图：

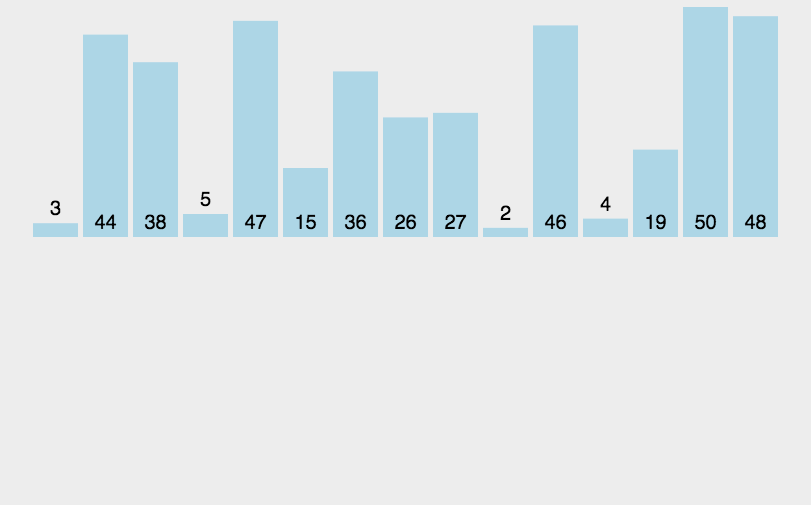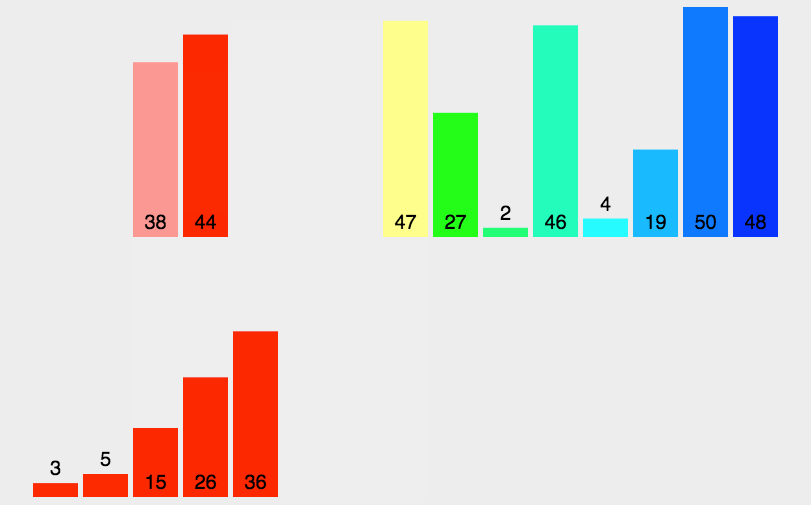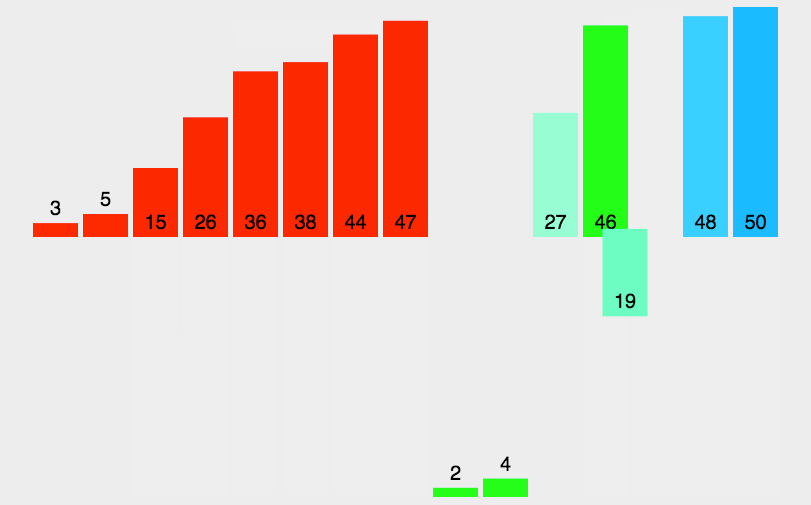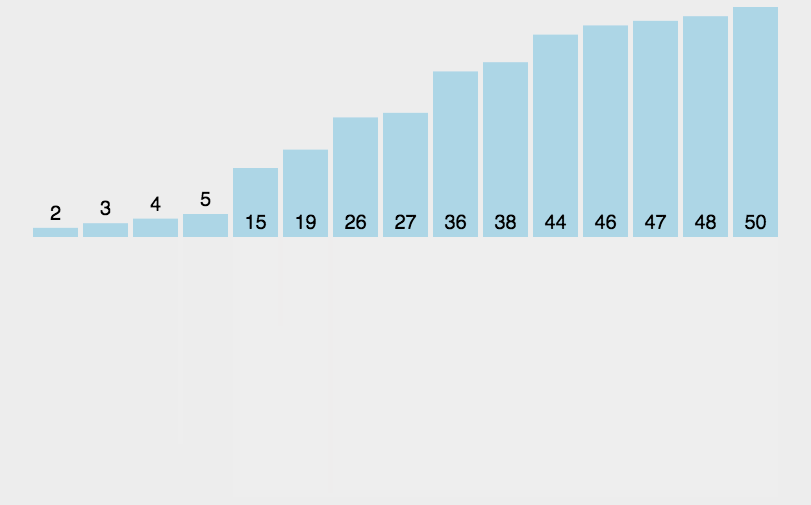
归并排序思想：

先对其划分区间，通过递归调用让其左边区间有序，在让其右边区间有序，最后在通过归并过程让其整体有序。

归并过程：我们先将其划分为左右两个区间，在设置两个指针，一个指针指向左区间开始位置，一个指针指向右区间开始位置，两个指针指向的元素进行比较谁小就拷贝谁，将其拷贝到一个临时数组中去，最后如果有剩余的元素没有拷贝到数组中，再将其拷贝到这个临时数组中，再把临时数组存放的元素拷贝回原数组当中。最后原数组有序

归并排序代码实现：

    public static void merge(int[] array,int left,int mid,int right){
         int b1 = left;
         int e1 = mid;
         int b2 = mid+1;
         int e2 = right;
          //合并成一个数组里面
         int[] tmp = new int[right-left+1];
         int k =0;
         while(b1<=e1&&b2<=e2){
             if(array[b1]<array[b2]){
                 tmp[k++] = array[b1++];
             }else {
                 tmp[k++] = array[b2++];
             }
         }
         while(b1<=e1){
             tmp[k++] = array[b1++];
         }
         while(b2<=e2){
             tmp[k++] = array[b2++];
         }
         for(int i =0;i<k;++i){
             array[i+left] = tmp[i];
         }
    }

    public static void mergeSort(int[] array,int left,int right){
        if(left>=right) return;
        int mid = left+((right-left)>>>1);
        mergeSort(array,left,mid);
        mergeSort(array,mid+1,right);
        merge(array,left,mid,right);
    }

归并排序非递归版本

非递归：依据归并排序原理，先让其一个一个有序，2个2个有序，然后4......到整体有序，我们可以模拟递归过程，每次都对其区间进行调整，然后调用归并过程让其有序，每次增量都在改变(1,2,4,.......)。

    public static void mergeSortNor(int[] array){
        //归并排序非递归实现
        int gap =1;
        while(gap<array.length){
            for(int i =0;i<array.length;i+=2*gap) {
                int left = i;
                int mid = left + gap - 1;
                if(mid>array.length-1){
                    mid = array.length-1;
                }
                int right = mid + gap;
                if(right>array.length-1){
                    right = array.length-1;
                }
                merge(array, left, mid, right);
            }
            gap*=2;
        }
    }

归并排序时间复杂度、空间复杂度、稳定性分析

时间复杂度：O(N*logN) 每一次归都要对每个元素进行让其有序，需要进行树的高度次

空间复杂度：O(N) 开辟临时数组辅助空间O(N),加上递归深度O(logN)--》O(n+logn)->O(N)

稳定性：稳定