前言

给定节点和边(节点对)，求关于连通分量及其变种。第一想法都是根据节点和节点对(边)来建立邻接矩阵，在DFS做事。
但还有一种和连通分量紧密相关的思想，并查集，它不建立完整的图，但能做相应的事，所以运行时间短。
它将原有的图，从中选出一个节点作为根节点，所有直接/间接相连的节点都作为子节点，能解很多连通分量/连通分量变种问题。
并查集除上述优点外，我感觉它的数组hash比hashMap快，毕竟数组为JVM层面，且连续内层分配，比API快。

一、统计无向图中无法互相到达点对数

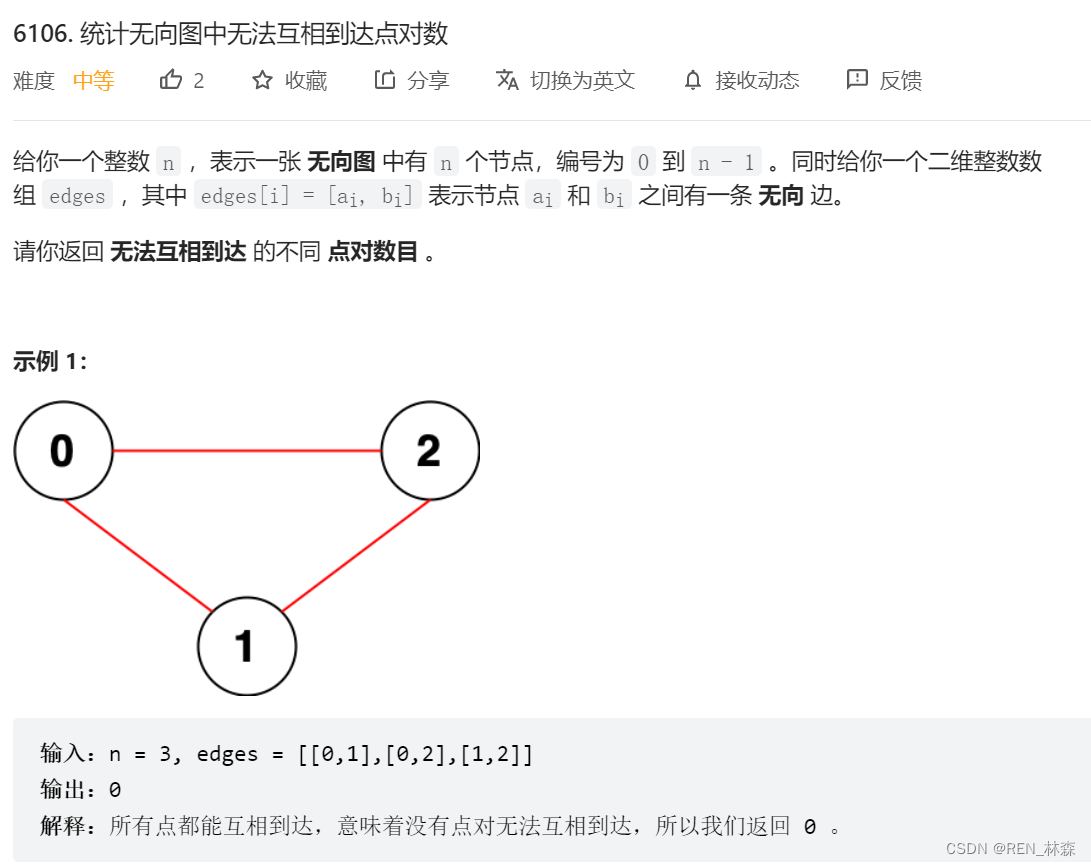
二、经典建邻接表+DFS统计 -> 并查集优化

1、经典建邻接表+DFS统计

public class CountPairs {
    public long countPairs(int n, int[][] edges) {
        // 加入所有节点。
        for (int i = 0; i < n; i++) addNode(i);
        for (int[] edge : edges) addEdge(edge[0], edge[1]);
        List<Long> arr = new ArrayList<>();
        for (int i = 0; i < n; i++) if (graph.containsKey(i)) arr.add(dfs(i));
        //
        long[] prefix = new long[arr.size()];
        long sum = 0, ans = 0;
        int idx = 0;

        for (long i : arr) prefix[idx++] = (sum += i);
        for (int i = 0; i < arr.size() - 1; i++) ans += arr.get(i) * (prefix[arr.size() - 1] - prefix[i]);
        return ans;
    }

    private long dfs(int n) {
        long rs = 1;
        Set<Integer> next = graph.get(n);
        if (next == null) return rs;
        graph.remove(n);
        for (Integer i : next) {
            if (graph.containsKey(i)) rs += dfs(i);
        }
        return rs;
    }

    private void addEdge(int a, int b) {
        addNode(a);
        addNode(b);

        graph.get(a).add(b);
        graph.get(b).add(a);
    }

    private void addNode(int b) {
        if (!graph.containsKey(b)) graph.put(b, new HashSet<>());
    }

    Map<Integer, Set<Integer>> graph = new HashMap<>();
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

2、并查集优化

// 练习哈并查集，它是关于连通分量的利器。
class CountPairs2 {
    public long countPairs(int n, int[][] edges) {
        // 并查集标准第一步：初始化。
        int[] father = new int[n];
        Arrays.fill(father, -1);
        // 并查集标准第二步：union
        cnt = n;// 这里想统计连通分量个数，方便等会统计每个连通分量的节点数，可以用到数组，而不是可扩容的list.| 也可直接list
        for (int[] edge : edges) union(father, edge[0], edge[1]);
        // 非特定逻辑，具体需求具体写。
        // 统计每个连通分量节点数。
        int[] arr = new int[cnt];
        cnt = 0;
        for (int f : father) if (f < 0) arr[cnt++] = -f;
        // 非特定逻辑，具体需求具体写。
        // 得到不同连通分量的节点数，利用前缀和，空间换时间。
        long[] prefix = new long[arr.length];
        long sum = 0;
        cnt = 0;
        for (int a : arr) prefix[cnt++] = (sum += a);
        // 得到结果
        long ans = 0;
        for (int i = 0; i < arr.length - 1; i++) ans += arr[i] * (prefix[prefix.length - 1] - prefix[i]);
        return ans;
    }

    int cnt = 0;// 连通分量个数。

    private void union(int[] father, int m, int n) {
        // 并查集标准第三步：findFather
        int r1 = findFather(father, m);
        int r2 = findFather(father, n);
        // 非同一逻辑，根据实际情况来写。
        if (r1 != r2) {
            // 合并两者，就将一个作为根，得到其整个树的节点数，这里负数表示。
            father[r1] += father[r2];
            // 并把另一个作为子树，并把其根节点修改。
            father[r2] = r1;
            // 可选操作，当用list时，则不必。
            --cnt;
        }
    }

    private int findFather(int[] father, int r) {
        // 一路返回根，并把根作为路径上每个节点的根.
        // 体现在 if (father[r] != r) father[r] = findFather(father, father[r]); return father[r];这将把有深度的树平铺起来。

        // 但是这里不行，因为根节点的值不是等于其下标，是负数，需要统计节点个数。
        // 这里需要一改传统做法，要灵活变通。

        // 若该节点是根
        if (father[r] < 0) return r;
        return father[r] = findFather(father, father[r]);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

总结

1）经典邻接表建立 + 在dfs遍历（图操作的基础）做各自事。
2）并查集将图的形状改掉，但不影响解题，则它降低的运行时间就变成了优点。
3）并查集除上述优点外，我感觉它的数组hash比hashMap快，毕竟数组为JVM层面，且连续内层分配，比API快。
4）并查集经典三步，每步都可因具体需求，而灵活变通写法。具体三步为：初始化数组father[size]{}(数组hash非常nice)、union(int[],int,int)联结两节点、findFather(int[],int)寻找根节点。

参考文献

[1] LeetCode 统计无向图中无法互相到达点对数