题目地址：

https://www.luogu.com.cn/problem/P5020

题目描述：
在网友的国度中共有$n$种不同面额的货币，第$i$种货币的面额为$a[i]$，你可以假设每一种货币都有无穷多张。为了方便，我们把货币种数为$n$、面额数组为$a[1..n]$的货币系统记作$(n,a)$。在一个完善的货币系统中，每一个非负整数的金额$x$都应该可以被表示出，即对每一个非负整数$x$，都存在$n$个非负整数$t[i]$满足$a[i]\times t[i]$的和为$x$。然而， 在网友的国度中，货币系统可能是不完善的，即可能存在金额$x$不能被该货币系统表示出。例如在货币系统$n=3,a=[2,5,9]$中，金额$1,3$就无法被表示出来。 两个货币系统$(n,a)$和$(m,b)$是等价的，当且仅当对于任意非负整数$x$，它要么均可以被两个货币系统表出，要么不能被其中任何一个表出。 现在网友们打算简化一下货币系统。他们希望找到一个货币系统$(m,b)$，满足$(m,b)$与原来的货币系统$(n,a)$等价，且$m$尽可能的小。他们希望你来协助完成这个艰巨的任务：找到最小的$m$。

输入格式：
输入文件的第一行包含一个整数$T$，表示数据的组数。
接下来按照如下格式分别给出$T$组数据。 每组数据的第一行包含一个正整数$n$。接下来一行包含$n$个由空格隔开的正整数$a[i]$。

输出格式：
输出文件共有$T$行，对于每组数据，输出一行一个正整数，表示所有与$(n,a)$等价的货币系统$(m,b)$中，最小的$m$。

数据范围：

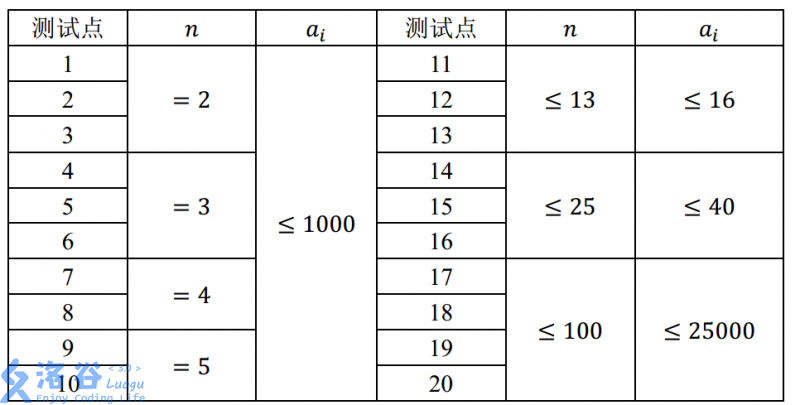
对于$100\%$的数据，满足$1\le T\le 20,n,a[i]\ge 1$。

思路参考https://blog.csdn.net/qq_46105170/article/details/114298230。代码如下：

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 110, M = 25010;
int n, a[N];
bool f[M];

int main() {
  int T;
  scanf("%d", &T);
  while (T--) {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
    sort(a + 1, a + 1 + n);

    memset(f, 0, sizeof f);
    f[0] = true;

    int res = 0;
    for (int i = 1; i <= n; i++) {
      if (!f[a[i]]) res++;
      // 看看新增一种货币a[i]能使得哪些数量得以表示
      for (int j = 0; j <= a[n] - a[i]; j++)
        f[j + a[i]] |= f[j];
    }

    printf("%d\n", res);
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

每组数据时间复杂度$O(n{\max }_i{a}_i)$，空间$O({\max }_i{a}_i)$。