6.1 - 6.2 公钥密码学简介

对称密码方案优点：

1. 加密、解密处理速度快，具有很高的数据吞吐率；
2. 密钥相对较短；
3. 硬件加密实现可达到几百兆字节每秒，软件也可以达到兆字节每秒的吞吐率。

对称密码方案缺点：

• 密钥分配问题；
• 密钥个数；
• 对Alice 或 Bob 的欺骗没有防御机制。

公钥算法的主要安全机制（优点）：

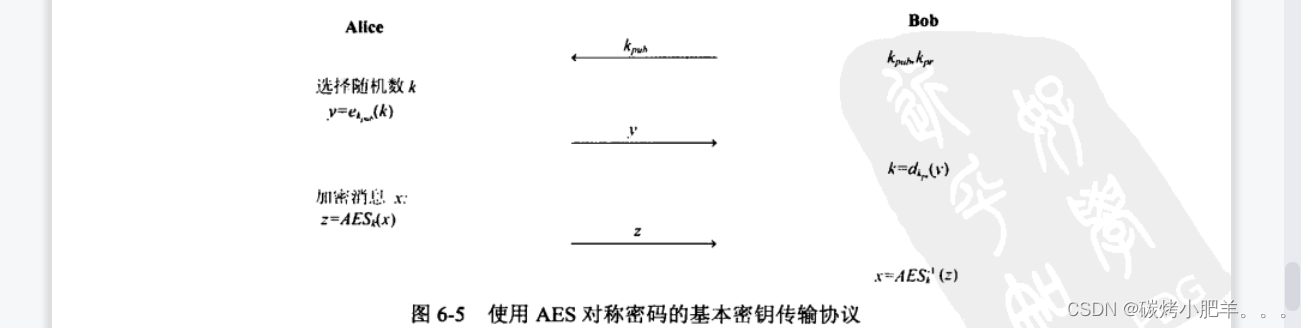
1. 密钥建立 在不安全信道上建立密钥的协议有若干种,包括 Diffie-Hellman密钥交换(DHKE)协议或RSA密钥传输协议。
2. 不可否认性 可以通过数字签名算法(比如 RSA、DSA 或ECDSA)实现不可否认性和消息完整性。
3. 身份标识 在类似银行智能卡或手机等的应用中,可使用质询-响应协议与数字签名相结合的方法识别实体。
4. 加密 可使用类似RSA 或Elgamal的算法对消息进行加密。

公钥方案的主要缺点：由于公钥算法的密钥非常长，导致使用公钥算法对数据进行加密的计算量非常大———通俗地说，就是非常慢。

函数f()是一个单项函数，仅当：

1. $y=f(x)$在计算上是很容易的，且
2. $x=f^{-1}(y)$在计算上是不可行的。
   

实际的公钥方案中常使用两种主流的单向函数：

1. 整数分解方案。 它是RSA的基础。给定两个大素数，计算它们的乘积非常容易;但是将它们的乘积分解因式却是非常困难的。
2. 离散对数方案。 离散对数方案有不少算法都基于有限域内的离散对数问题，最典型的例子包括Diffie-Hellman密钥交换、Elgamal加密或数字签名算法(DSA)。
3. 椭圆曲线(EC)方案。 离散对数算法的一个推广就是椭圆曲线公钥方案。典型例子包括椭圆曲线Diffie-Hellman密钥交换(ECDH)和椭圆曲线数字签名算法(ECDSA)。

密钥等级与安全等级：

“n位安全等级”： 如果已知最好的攻击需要$2^n$步才能破解某个算法，则这个算法可以称为拥有“n位安全等级”。这个定义非常容易理解，因为安全等级为n的对称算法对应的密钥长度也为n位。非对称算法的密码强度与安全性之间的关系没有这么直观。下表显示了位数为80、128、192和256的四个安全等级对应的公钥算法推荐使用的位长度。从表中可以看出，类似RSA的方案和离散对数方案都需要非常长的