如何通俗地理解合同矩阵 - 码农知识堂

如何通俗地理解合同矩阵

如何通俗地解释合同矩阵

同一个二次曲线，在不同基下需要用不同的二次型矩阵表示。这两个二次型矩阵就称为合同矩阵。

1 解释

1.1 直角坐标系

假设我们有这样一个椭圆,它在直角坐标系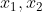下的对应方程为

1.2 自然基

下面，我们这个方程用二次型表示为

$[\boldsymbol{x}]_\mathcal{E}^T \boldsymbol{A}[\boldsymbol{x}]_\mathcal{E}=1$

其中 $[\boldsymbol{x}]_\mathcal{E}$ 就是椭圆上的点在自然基下的坐标

1.3 非自然基

既然椭圆可以表示在自然基下，当然也可以表示在非自然基下

假设椭圆在某非自然基的对应方程为

$[\boldsymbol{x}]_\mathcal{P}^T \boldsymbol{B}[\boldsymbol{x}]_\mathcal{P}=1$

$[\boldsymbol{x}]_\mathcal{P}$ 就是椭圆上的点在非自然基下的坐标

1.4 合同矩阵

可以看到， $\boldsymbol{A},\boldsymbol{B}$ 是同一个椭圆在不同基下对应的二次型,它们就被称为合同矩阵。

而我们知道，若 $\boldsymbol{A},\boldsymbol{B}$ 满足

$\boldsymbol{B}=\boldsymbol{P}^T\boldsymbol{A}\boldsymbol{P}$

它们才能称为合同阵,那这又是怎么得来的呢？下面我们就来推导一下

2 验证

假设由自然基到非自然基的过渡矩阵为 $\boldsymbol{P}$

首先，根据坐标变换公式有

$[\boldsymbol{x}]_\mathcal{E}=\boldsymbol{P}[\boldsymbol{x}]_\mathcal{P}$

然后，将这个式子与左边的椭圆方程联立

最后，令

$\boldsymbol{B}=\boldsymbol{P}^T\boldsymbol{A}\boldsymbol{P}$

这样，我们就得到了上面那幅图中，曲线在非自然基下的表达式

$[\boldsymbol{x}]_\mathcal{P}^T\boldsymbol{B}[\boldsymbol{x}]_\mathcal{P}=1$

3 例题

例:已知某曲线 ,在直角坐标系下的方程为 $\frac{5}{8}x_1^2-\frac{3}{4}x_1x_2+\frac{5}{8}x_2^2=1$ ,现将坐标系逆时针旋转 $\frac{\pi}{4}$ ,形成新的坐标系。

求此曲线在坐标系下的表达式

3.1 分析

本题，我们可以利用合同矩阵的知识来做

(1)首先,将曲线用向量形式，表示在自然基下

(2)然后,利用过渡矩阵，对向量空间进行换基

(3)最后,再将新的基下的曲线写回一般方程的形式

这样，我们可以就利用黄色路径来完成题目

3.2 求解

解:(1)令自然基下的坐标向量为 $[\boldsymbol{x}]_\mathcal{E}=\begin{pmatrix}x_1\\x_2\end{pmatrix}$ ,则 $\frac{5}{8}x_1^2-\frac{3}{4}x_1x_2+\frac{5}{8}x_2^2=1$ 在自然基下可以表示为

$\begin{pmatrix}x_1&x_2\end{pmatrix}\begin{pmatrix}\frac{5}{8}&-\frac{3}{8}\\-\frac{3}{8}&\frac{5}{8}\end{pmatrix}\begin{pmatrix}x_1\\x_2\end{pmatrix}=1$

(2)令非自然基的坐标向量为 $[\boldsymbol{x}]_\mathcal{P}=\begin{pmatrix}y_1\\y_2\end{pmatrix}$ ,则

$\begin{pmatrix}x_1\\x_2\end{pmatrix}=\boldsymbol{P}\begin{pmatrix}y_1\\y_2\end{pmatrix}$

其中 $\boldsymbol{P}$ 为旋转矩阵

$\boldsymbol{P}=\begin{pmatrix}\cos \frac{\pi}{4}&-\sin \frac{\pi}{4}\\\sin \frac{\pi}{4}&\cos \frac{\pi}{4}\end{pmatrix}=\begin{pmatrix}\frac{\sqrt{2}}{2}&-\frac{\sqrt{2}}{2}\\\frac{\sqrt{2}}{2}&\frac{\sqrt{2}}{2}\end{pmatrix}$

那么曲线在非自然基下的表达式为

$[\boldsymbol{x}]_\mathcal{P}^T\boldsymbol{P}^T\boldsymbol{A}\boldsymbol{P}[\boldsymbol{x}]_\mathcal{P}=1$

带入数据,整理后可得

$\begin{pmatrix}y_1&y_2\end{pmatrix}\begin{pmatrix}\frac{1}{4}&0\\0&1\end{pmatrix}\begin{pmatrix}y_1\\y_2\end{pmatrix}=1$

这里的 $\begin{pmatrix}\frac{1}{4}&0\\0&1\end{pmatrix}$ 就是 $\begin{pmatrix}\frac{5}{8}&-\frac{3}{8}\\-\frac{3}{8}&\frac{5}{8}\end{pmatrix}$ 的合同矩阵

(3)最后将非自然基下这个矩阵方程写回坐标系,得到曲线在下的表达式为

$\frac{1}{4}y_1^2+y_2^2=1$
相关阅读:
Leetcode 2099. Find Subsequence of Length K With the Largest Sum [Python]
用户案例 | 珍岛集团基于 Apache DolphinScheduler 打造智能营销云平台
 基于SpringBoot+Vue的服装销售系统
 js将两张图片合并成一张图片
 TairSearch：加速多列索引查询
 reflect 与 func
MySQL篇---第三篇
 嵌入式学习之Linux驱动（第九期_设备模型_教程更新了）_基于RK3568
【七夕特别篇】七夕已至，让爱闪耀
 反片语 set+哈希表就C++代码而言，我很短
原文地址：https://blog.csdn.net/ccnt_2012/article/details/125390368