题面

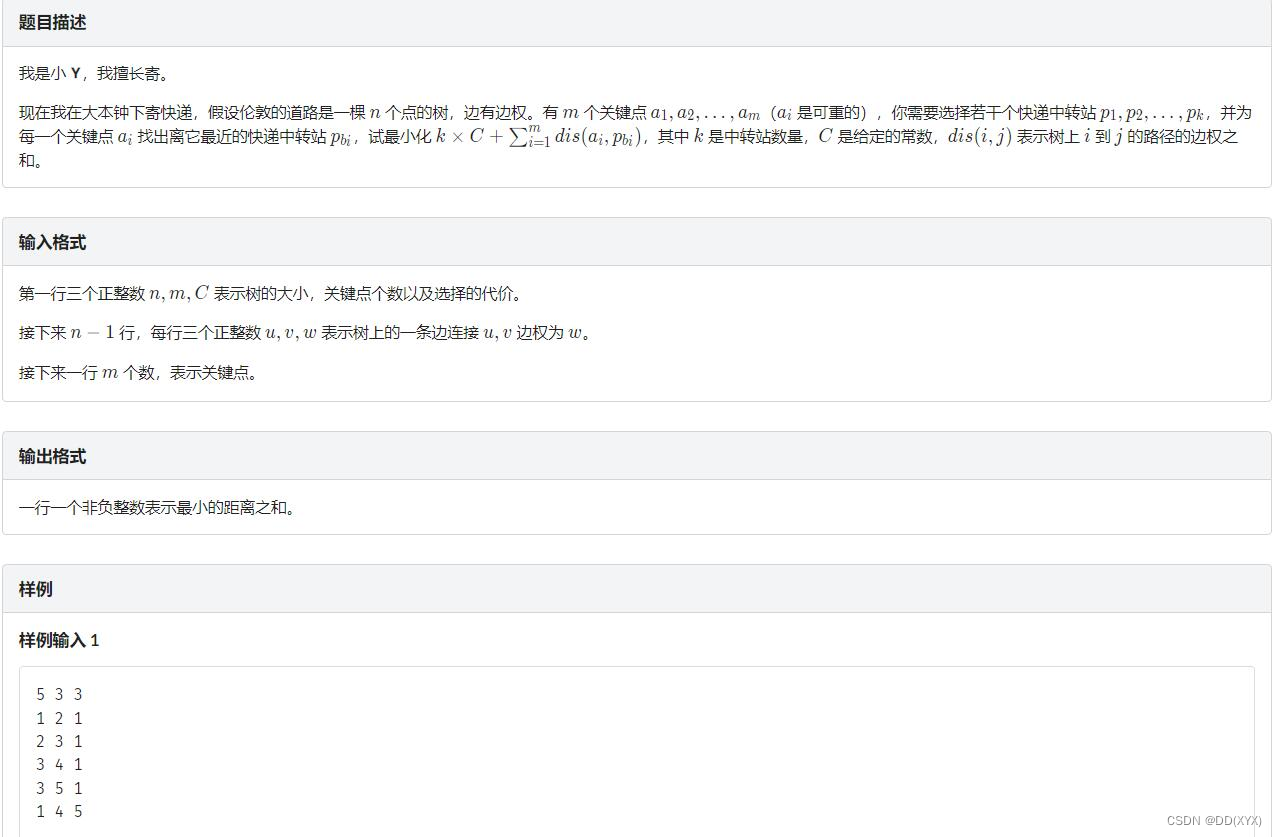
题解

找出最近的中转站可以直接转化为随便匹配一个中转站。

树形DP，这个没什么好说的。

主要是状态怎么设计。

正解以及大部分人设计的状态非常⭐，所以不需要什么别的东西直接可过。

但是我设计了个不太好的 DP：

令 $d{p}_1[i][j]$ 表示在 $i$ 的子树内，目前有 $j$ 个关键点无主，子树内所有边贡献和的最小值。$d{p}_2[i][j]$ 表示在 $i$ 子树外总共有 $j$ 个关键点要连进来，子树内所有边贡献和的最小值。

合并两个子树 $x,y$ 时，两个 DP 可以分别单独背包转移，除此之外，$d{p}_2[x][i]$ 还可以从 $d{p}_2[x/y][i+j]+d{p}_1[y/x][j]+...$ 转移过来。贪心的想，我们只需要往外的需求吞掉无主的需求，这时候无主的关键点一定不用多出来。最后再讨论一下在子树的根处设中转站。

但是有个小问题：每个子树的状态数都是抵满 $O(n)$ 的，虽然 $d{p}_1$ 的复杂度可以保证是 $O(n^2)$ ，但是 $d{p}_2$ 是 $O(n^3)$ 的。再次利用贪心技巧：子树外的需求总量不会超过子树内关键点总数，不然中转站可以上移。

时间复杂度 $O(n^2)$ 。

CODE

#include<map>
#include<set>
#include<cmath>
#include<ctime>
#include<queue>
#include<stack>
#include<random>
#include<bitset>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<unordered_map>
#pragma GCC optimize(2)
using namespace std;
#define MAXN 3005
#define LL long long
#define ULL unsigned long long
#define ENDL putchar('\n')
#define DB double
#define lowbit(x) (-(x) & (x))
#define FI first
#define SE second
#define PR pair<int,int>
int xchar() {
	static const int maxn = 1000000;
	static char b[maxn];
	static int pos = 0,len = 0;
	if(pos == len) pos = 0,len = fread(b,1,maxn,stdin);
	if(pos == len) return -1;
	return b[pos ++];
}
// #define getchar() xchar()
LL read() {
	LL f = 1,x = 0;int s = getchar();
	while(s < '0' || s > '9') {if(s<0)return -1;if(s=='-')f=-f;s = getchar();}
	while(s >= '0' && s <= '9') {x = (x<<1) + (x<<3) + (s^48);s = getchar();}
	return f*x;
}
void putpos(LL x) {if(!x)return ;putpos(x/10);putchar((x%10)^48);}
void putnum(LL x) {
	if(!x) {putchar('0');return ;}
	if(x<0) putchar('-'),x = -x;
	return putpos(x);
}
void AIput(LL x,int c) {putnum(x);putchar(c);}

int n,m,s,o,k;
int hd[MAXN],nx[MAXN<<1],v[MAXN<<1],w[MAXN<<1],cne;
void ins(int x,int y,int z) {
	nx[++cne] = hd[x]; v[cne] = y; hd[x] = cne; w[cne] = z;
}
LL dp[MAXN][MAXN],dp2[MAXN][MAXN],td[MAXN],td2[MAXN];
int siz[MAXN],ct[MAXN],C;
void dfs(int x,int ff) {
	siz[x] = ct[x];
	for(int i = 0;i <= n;i ++) dp[x][i] = 1e18,dp2[x][i] = 1e18;
	dp[x][0] = C; dp[x][ct[x]] = 0;
	for(int i = 0;i <= ct[x];i ++) dp2[x][i] = C;
	for(int ii = hd[x];ii;ii = nx[ii]) {
		int y = v[ii],W = w[ii]; if(y == ff) continue;
		dfs(y,x);
		for(int i = siz[x];i >= 0;i --) {
			td[i] = dp[x][i],td2[i] = dp2[x][i];
			dp[x][i] = 1e18; dp2[x][i] = 1e18;
		}
		for(int i = siz[x];i >= 0;i --) {
			for(int j = siz[y];j >= 0;j --) {
				dp[x][i+j] = min(dp[x][i+j],td[i] + dp[y][j] + W*1ll*j);
				dp2[x][i+j] = min(dp2[x][i+j],td2[i] + dp2[y][j] + W*1ll*j);
			}
			for(int j = 0;j <= siz[y] && j <= i;j ++) {
				dp2[x][i-j] = min(dp2[x][i-j],td2[i] + dp[y][j] + W*1ll*j);
			}
		}
		for(int i = siz[y];i >= 0;i --) {
			for(int j = 0;j <= siz[x] && j <= i;j ++) {
				dp2[x][i-j] = min(dp2[x][i-j],dp2[y][i] + W*1ll*i + td[j]);
			}
		}
		siz[x] += siz[y];
	}
	LL mn = 1e18;
	for(int i = 0;i <= siz[x];i ++) mn = min(mn,dp[x][i] + C);
	dp2[x][0] = dp[x][0] = min(min(dp2[x][0],dp[x][0]),mn);
	for(int i = 1;i <= siz[x];i ++) dp2[x][i] = min(dp2[x][i],mn);
	return ;
}
int main() {
	freopen("post.in","r",stdin);
	freopen("post.out","w",stdout);
	n = read(); m = read(); C = read();
	for(int i = 1;i < n;i ++) {
		s = read();o = read();k = read();
		ins(s,o,k); ins(o,s,k);
	}
	for(int i = 1;i <= m;i ++) {
		ct[read()] ++;
	}
	dfs(1,0);
	AIput(dp[1][0],'\n');
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104