Python中的集合(set)是一个无序的不重复元素序列，如果在初始化时有重复的元素，重复的元素会被合并处理。
可以使用花括号 { } 或者 set() 函数创建集合，注意：创建一个空集合必须用 set() 而不是 { }，因为 { } 是用来创建一个空字典。

接下来，通过示例来学习Python中的集合(set)及其操作方法。

声明：博主(昊虹图像算法)写这篇博文时，用的Python的版本号为3.9.10。

01-集合(set)的创建及重复元素的自动合并

创建方法有两种：

parame = {value01,value02,...}
1

或

set(value)
1

示例代码如下：

set1 = {'pear', 'banana', 'orange', 'apple'}

set2 = {'apple', 'orange', 'apple', 'pear', 'orange', 'banana'}

set3 = set('abracadabra')

set4 = set('abcdefg')
1
2
3
4
5
6
7

运行结果如下：

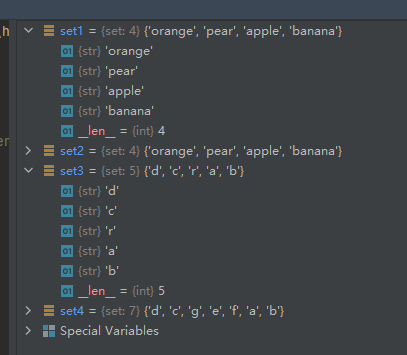
从上面的运行结果可以看出，set2和set3中的重复元素都被合并了。
对比列表的存储结构：

我们是不是可以作这样一种推测：集合中的元素不分顺序？答：是的，Python集合的特点之一就是无序性。

02-使用方法add()往集合中添加一个元素

示例代码如下：

set1 = {'pear', 'banana', 'orange', 'apple'}
set1.add('kkk')
1
2

运行结果如下：

03-使用方法update()往集合中添加多个元素

set1 = {'pear', 'banana', 'orange', 'apple'}
set1.update({'kkk', 'ppp'})
1
2

运行结果如下：

04-使用方法remove()和discard()将指定元素从集合中移除

示例代码如下：

set1 = {'pear', 'banana', 'orange', 'apple'}
set1.remove('pear')

set2 = {'pear', 'banana', 'orange', 'apple'}
set2.remove('orange')
1
2
3
4
5

运行结果如下：

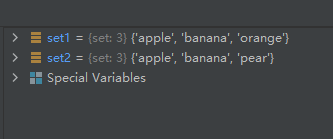
方法remove()和方法discard()的区别在于，方法remove()在移除元素时，如果元素不存在，会报错，中止程序运行，而方法discard()不会。

05-使用方法pop()随机删除集合中的一个元素

示例代码如下：

set1 = {'pear', 'banana', 'orange', 'apple'}
set1.pop()
1
2

运行两次，结果如下：
第一次：

第二次：

可见，第一次随机删除的是元素’banana’，第二次随机删除的是元素’orange’。
实际上， pop()方法会对集合进行无序的排列，然后将这个无序排列集合的左面第一个元素进行删除。所以我们看到原集合中元素的相对位置都变了。

06-使用函数len()得到集合中元素的个数

示例代码如下：

set1 = {'pear', 'banana', 'orange', 'apple'}

count1 = len(set1)
1
2
3

运行结果如下：

07-使用方法clear()清空集合

示例代码如下：

set1 = {'pear', 'banana', 'orange', 'apple'}
set2 = {'pear', 'banana', 'orange', 'apple'}
set1.clear()

1
2
3
4

运行结果如下：

08-使用“in”判断元素是否在集合里

示例代码如下：

set1 = {'pear', 'banana', 'orange', 'apple'}
bool1 = 'apple' in set1
bool2 = 'swh' in set1
1
2
3

运行结果如下：

09-使用方法difference() 或运算符“-”返回两个集合的差集

方法difference() 返回两个集合的差集，差集是指这个集合的元素在集合x中，但不在集合y中。
设z表示集合x与y的差集，则z=x-(x∩y)。

示例代码如下：

x = {"apple", "banana", "cherry"}
y = {"apple", "google", "microsoft"}

z1 = x.difference(y)
z2 = x-y
1
2
3
4
5

运行结果如下：

10-使用方法difference_update()将原集合与另一集合的交集元素去掉【实质上还是求差集】

方法difference_update()实际上和方法difference()做的是同样的运算，只是方法difference()做的是运算：z=x-(x∩y) 而方法difference_update()做的是运算：x=x-(x∩y)
示例代码如下：

x = {"apple", "banana", "cherry"}
y = {"apple", "google", "microsoft"}

x.difference_update(y)
1
2
3
4

运行结果如下：

11-使用方法intersection()、intersection_update()和运算符“&”求两集合的交集

方法intersection()有返回值，而方法intersection_update()没有返回值。
示例代码如下：

x1 = {"apple", "banana", "cherry"}
x2 = {"apple", "banana", "cherry"}
y = {"apple", "google", "microsoft"}

z1 = x1.intersection(y)
z2 = x1 & y

x2.intersection_update(y)
1
2
3
4
5
6
7
8

运行结果如下：

12-使用方法isdisjoint()判断原集合中是不是不包含另一集合中的任一元素(判断两个集合是否包含相同的元素)

isdisjoint() 方法用于判断两个集合是否包含相同的元素，如果没有返回 True，否则返回 False。。
示例代码如下：

x = {'apple', 'banana', 'cherry'}
y1 = {'apple', 'google', 'microsoft'}
y2 = {'facebook', 'google', 'microsoft'}

bool1 = x.isdisjoint(y1)
bool2 = x.isdisjoint(y2)

1
2
3
4
5
6
7

运行结果如下：

分析：y1中有x中的元素’apple’，所以bool1值为False; y2中没有x中的元素，所以bool2值为True。

13-使用方法issubset()判断原集合是否是另一集合的子集

示例代码如下：

x = {"a", "b", "c"}
y1 = {"f", "e", "d", "c", "b", "a"}
y2 = {"f", "e", "d", "g", "h", "m"}

bool1 = x.issubset(y1)
bool2 = x.issubset(y2)

1
2
3
4
5
6
7

运行结果如下：

14-使用方法issuperset()判断另一集合是否是原集合的子集

示例代码如下：

x = {'a', 'b', 'c', 'd', 'e', 'f'}
y1 = {'a', 'b', 'c'}
y2 = {'g', 'h', 'i'}

bool1 = x.issuperset(y1)
bool2 = x.issuperset(y2)

1
2
3
4
5
6
7

运行结果如下：

15-使用方法symmetric_difference()、运算符“^”和symmetric_difference_update()得到两个集合中不重复的元素集合。

方法symmetric_difference()和运算符“^”是等价的，所以下面对方法symmetric_difference()的介绍就是对运算符“^”的介绍。
设两个集合为x，y，z是方法symmetric_difference()的结果，则：
z=[x-(x∩y)]+[y-(x∩y)]
示例代码如下：

x = {1, 2, 3, 4, 5, 6}
y = {1, 2, 3, 7, 8, 9}

z1 = x.symmetric_difference(y)
z2 = x ^ y

1
2
3
4
5
6

运行结果如下：

方法symmetric_difference_update()和symmetric_difference()做的运算是一样的，惟一的区别是symmetric_difference_update()无返回值，symmetric_difference()有返回值：
symmetric_difference()的运算式如下：
z=[x-(x∩y)]+[y-(x∩y)]
而symmetric_difference_update()的运算式如下：
x = [x-(x∩y)]+[y-(x∩y)]
示例代码如下：

x = {1, 2, 3, 4, 5, 6}
y = {1, 2, 3, 7, 8, 9}

x.symmetric_difference_update(y)

1
2
3
4
5

16-使用函数union()或运算符“|”返回多个集合的并集

示例代码如下：

x1 = {1, 2}
x2 = {3, 4}
x3 = {5, 6}
x4 = {7, 8}

y1 = set.union(x1, x2, x3)
y2 = set.union(x1, x2, x3, x4)

y3 = x1 | x2 | x3
y4 = x1 | x2 | x3 | x4
1
2
3
4
5
6
7
8
9
10

运行结果如下：

17-使用方法copy()复制集合

示例代码如下：

fruits = {"apple", "banana", "cherry"}

x = fruits.copy()
1
2
3

运行结果如下：

参考资料：
https://blog.csdn.net/wenhao_ir/article/details/125100220