哈喽~大家好呀，期末考试终于结束了，暑假准备去哪里玩呀？假期期间大家别忘了来充实自己，注意防疫安全。那么接下来我们的算法合集第三篇来了（题外话：最近肝的心疼~），今天我们来看看这篇最有趣的算法（三）数论篇吧。

 🥇个人主页：个人主页​​​​​             

🥈 系列专栏：【算法】           

🥉与这篇相关的文章：            

恭喜你~遇到了最有趣的排序算法（一）	恭喜你~遇到了最有趣的排序算法（一）_程序猿追的博客-CSDN博客
恭喜你~遇到了最有趣的算法（二）	恭喜你~遇到了最有趣的算法（二）_程序猿追的博客-CSDN博客
操作系统中几种最最最常见的调度算法	操作系统中几种最最最常见的调度算法（适用于软件设计师考试与期末考试复习）_程序猿追的博客-CSDN博客_操作系统先进先出算法例题

目录

一、 欧几里得算法

二、扩展欧几里得算法

三、求素数问题

3.1 试除法

3.2 朴素版的筛素数

3.3 埃式筛法

3.4 线性筛法

3.5 比较快的判断素数的方法

四、欧拉函数

---

一、 欧几里得算法

✅欧几里得算法又称辗转相除法，是指用于计算两个非负整数a，b的最大公约数。

✨作用：求两个正整数的最大公约数。

🎀时间复杂度： O(logn)。

int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}

我们这里求了最大公约数那么最小公倍数就不要落下了

int lcm(int a, int b)
{
    return a * b / gcd(a, b);
}

二、扩展欧几里得算法

✅这里我们有一个定理

裴蜀定理：若 a, b是整数,且 (a, b) = d，那么对于任意的整数 x, y, ax + by 都一定是 d 的倍数，特别地，一定存在整数 x, y使 ax + by = d成立。

✨也就是说我们给出 a，b 来求出 x，y 的值。 

🎀时间复杂度： O(logn)

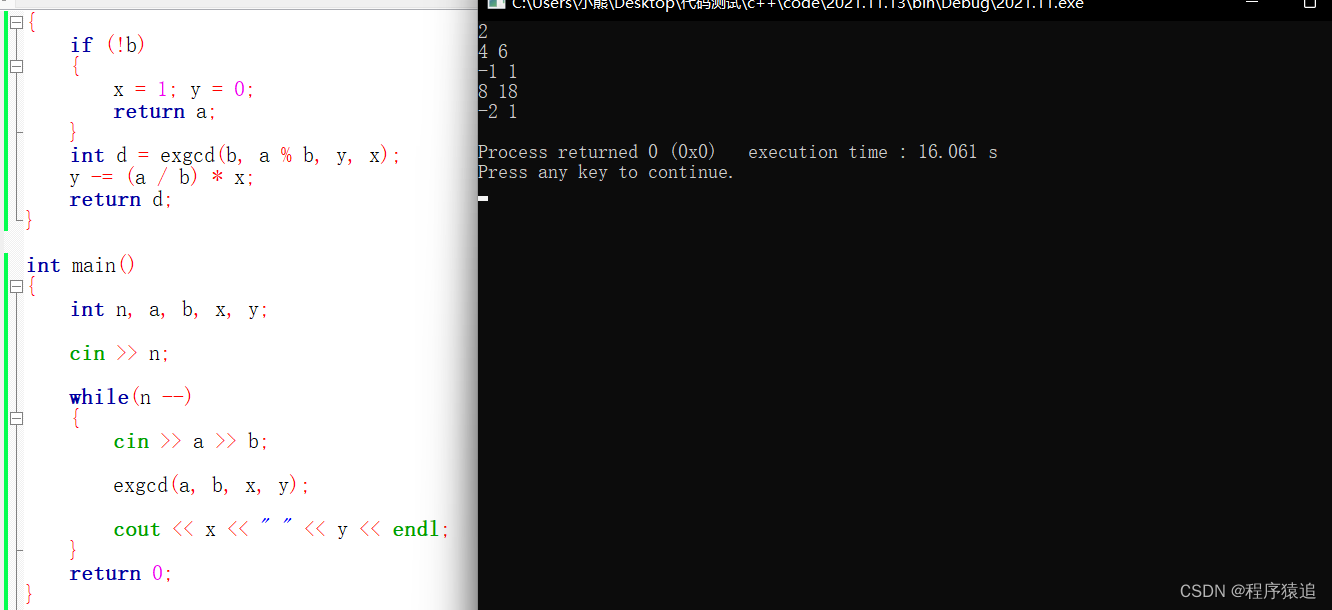
int exgcd(int a, int b, int &x, int &y)
{
    if (!b)
    {
        x = 1; y = 0;
        return a;
    }
    int d = exgcd(b, a % b, y, x);
    y -= (a/b) * x;
    return d;
}

 我们直接上题目

 

 三、求素数问题

✅素数问题是我们经典的题，什么是素数？

素数一般指质数。质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数

✨说明：以下 primes[N]，cnt是属于 int 数组，st[N] 是属于 bool 数组，而 N 是 const 定义的大小。

🎀primes 就是用来装素数的，cnt 用来计数的，st 用来记录是否是素数的。

3.1 试除法

bool sushu(int n)
{
    if(n == 1) return false;
 
    for(int i = 2; i <= n / i; i ++)
        if(n % i == 0)
            return false;
 
    return true;
}

 

这是我们通常的做法，也是最容易理解的做法。 

3.2 朴素版的筛素数

void get_primes1(int n) 
{
    for(int i = 2; i <= n; i++) 
    {
        if(!st[i]) prime[cnt ++] = i;
        for(int j = i + i; j <= n; j += i)
            st[j] = true;
    }
}

通过 st 数组的 true 与 false 来区分是否是素数。 

3.3 埃式筛法

✅以上我们知道了如何判断素数，但在一区间里面例如 2 ~ 10 里面有多少个素数呢？那么接下来我们来看看。

void get_primes2(int n) 
{
    for(int i = 2; i <= n; i++) 
    {
        if(!st[i])
        { 
            prime[cnt ++] = i;
            for(int j = i; j <= n; j += i)
                st[j] = true;
        }
    } 
}

🎀但我们明显发现时间复杂度为O（nlogn），太~高了，很容易 TLE，那么如何提速呢？看看下面的线性筛法吧。

3.4 线性筛法

✅在 O(n) 的时间复杂度内求出 1∼n 之间的所有质数。

void get_prime(int n) 
{
    for(int i = 2; i <= n; i++) 
    {
        if(!st[i]) prime[cnt++] = i;
        for(int j = 0; prime[j] <= n / i; j++)
        {
            st[prime[j] * i] = true;
            if(i % prime[j] == 0) break;
        }
    }
} 

✨这里的用法就和上面的一模一样了，我就不展示了。 

3.5 比较快的判断素数的方法

bool ispri(int k) 
{
    if(k <= 1) return false;
    if(k <= 3) return true;
    if(k % 6 != 1 && k % 6 != 5) return false;
    for(int i = 5;i < k / i;i += 6) {
        if(k % i == 0 || k % (i + 2) == 0) return false;
    }
    return true;
}

四、欧拉函数

✅欧拉函数，一般记为 ϕ(n)，表示小于等于 n 的数中与 n 互质的数的个数。

void get_eulers(int n)
{
    euler[1] = 1;
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i])
        {
            primes[cnt ++ ] = i;
            euler[i] = i - 1;
        }
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0)
            {
                euler[i * primes[j]] = euler[i] * primes[j];
                break;
            }
            euler[i * primes[j]] = euler[i] * (primes[j] - 1);
        }
    }
}

看到这里，首先在这里感谢大家，谢谢大家对我的支持，我创建了一套专栏——Java学习之路(零基础到就业实战)，感兴趣的可以去看看，接下来暑假的时间，我会把这套专栏认真学好写好，我们一起努力向着更好的自己前进，冲冲冲！

 （求关注）持续更新中……