“山大地纬杯”第十二届山东省ICPC大学生程序设计竞赛

打星队的菜比来补题啦

A - Seventeen（构造，签到）

用1~n所有数字用+，-，*，(，)，组成计算式使得其得数为17。

思路：找规律可得，小于4绝对无法组成17，当n为4时，可使得(4+1)*3+2得出17，n为5时，可使得4*5-3*(2-1)，对于n为偶数时，可以以4为基础，剩下的相邻两数两两组成(i+1-i)的形式得到1，从而对答案无影响；n为奇数时，则以5为基础，相同操作即可。

AC Code：

#include <bits/stdc++.h>
 
typedef long long ll;
const int N=2e5+5;
int n;
 
int main(){
	std::ios::sync_with_stdio(false);
	std::cin.tie(0);
	std::cin>>n;
	if(n<4){
		std::cout<<-1<<'\n';
		return 0;
	}
	if(n%2==0){
		std::cout<<"(4+1)*3+2";
		for(int i=5;i<=n;i+=2){
			std::cout<<"*("<<i+1<<"-"<<i<<")";
		}
		std::cout<<'\n';
	}
	else{
		std::cout<<"4*5-3*(2-1)";
		for(int i=6;i<=n;i+=2){
			std::cout<<"*("<<i+1<<"-"<<i<<")";
		}
		std::cout<<'\n';
	}
	return 0;
}

os：这种类型的题之前师哥给的题中有类似的，但是我没有及时想到，在做的时候也很长时间没想到4是最小的界限，使得WA了好多发，，就离谱

K - Coins（规律，暴力枚举）

A有4种硬币2,3,17,19，B有4种硬币5,7,11,13，有若干组询问x，问谁能用更少的硬币凑出x。

思路：若同时有a和b两种面值的硬币，且a<b，则每a个b硬币可以用b个a硬币代替，故a硬币在最优解中小于b，所以对于比较小的范围我们可以暴力枚举得到答案，在一个较大的数情况下答案是一定的。

AC Code：

#include <bits/stdc++.h>
 
#define INF 0x3f3f3f3f
typedef long long ll;
const int N=1e5+5;
int A[]={0,2,3,17,19};
int B[]={0,5,7,11,13};
int a[N],b[N];
int x,q;
 
int main(){
	std::ios::sync_with_stdio(false);
	std::cin.tie(0);
	memset(a,INF,sizeof(a));
	memset(b,INF,sizeof(b));
	a[0]=0,b[0]=0;
	for(int i=1;i<=4;i++){
		for(int j=A[i];j<=100000;j++){
			a[j]=std::min(a[j],a[j-A[i]]+1);
		}
	}
	for(int i=1;i<=4;i++){
		for(int j=B[i];j<=100000;j++){
			b[j]=std::min(b[j],b[j-B[i]]+1);
		}
	}
	std::cin>>q;
	while(q--){
		std::cin>>x;
		if(x>=100000){
			std::cout<<"A"<<'\n';
			continue;
		}
		if(a[x]>=INF&&b[x]>=INF){
			std::cout<<-1<<'\n';
		}
		else if(a[x]==b[x]){
			std::cout<<"both"<<'\n';
		}
		else if(a[x]>b[x]){
			std::cout<<"B"<<'\n';
		}
		else if(a[x]<b[x]){
			std::cout<<"A"<<'\n';
		}
	}
	return 0;
}

os：这个题当时搞了好久到最后终于搞出来了，结果重测的时候被卡了，寄

H - Counting（桶维护）

给出k个人的初始坐标， 给出k个人在T秒内的动作，计算每一秒重叠的人的对数。

思路：直接模拟，每次走之后修改当前状态和下一个状态，注意人的对数是C(n,2)。

AC Code：

#include <bits/stdc++.h>
 
#define INF 0x3f3f3f3f
typedef long long ll;
const int N=3e3+5;
const int M=2e3+5;
int n,m,T,k;
int ans[N],x[M],y[M],mp[M][M];
char s[M][N];
 
int main(){
	scanf("%d%d%d%d",&n,&m,&k,&T);
	for(int i=0;i<k;i++){
		scanf("%d%d",&x[i],&y[i]);
		ans[0]-=(mp[x[i]][y[i]]-1)*mp[x[i]][y[i]]/2;
		mp[x[i]][y[i]]++;
		ans[0]+=(mp[x[i]][y[i]]-1)*mp[x[i]][y[i]]/2;
	}
	for(int i=0;i<k;i++){
		scanf("%s",s[i]);
	}
	int cnt=1;
	for(int j=0;j<T;j++){
		ans[cnt]=ans[cnt-1];
		for(int i=0;i<k;i++){
			ans[cnt]-=(mp[x[i]][y[i]]-1)*mp[x[i]][y[i]]/2;
			mp[x[i]][y[i]]--;
			ans[cnt]+=(mp[x[i]][y[i]]-1)*mp[x[i]][y[i]]/2;
			if(s[i][j]=='U') x[i]--;
			else if(s[i][j]=='D') x[i]++;
			else if(s[i][j]=='R') y[i]++;
			else if(s[i][j]=='L') y[i]--;
			ans[cnt]-=(mp[x[i]][y[i]]-1)*mp[x[i]][y[i]]/2;
			mp[x[i]][y[i]]++;
			ans[cnt]+=(mp[x[i]][y[i]]-1)*mp[x[i]][y[i]]/2;
		}
		++cnt;
	}
	for(int i=0;i<=T;i++){
		printf("%d\n",ans[i]);
	}
	return 0;
}

os：当时做题的时候队友开的计算几何，这个题看都没看，，，完完全全签到啊呜呜呜

E - Subsegments（思维，桶）

 给定数组a和一个数x，问有多少区间的乘积在模这个东西下得数为x。

思路：分两种情况讨论：x==0时，计算包含0的区间即可，注意不仅仅是数组中是0，模那个东西等于0也算；x不等于0时，同样以0为分界，对每一段维护前缀积，用map维护桶即可。

AC Code：

#include <bits/stdc++.h>
 
#define INF 0x3f3f3f3f
typedef long long ll;
const int N=5e5+5;
const int mod=998244353;
ll n,x,b,res,ans;
ll a[N];
 
int main(){
	std::ios::sync_with_stdio(false);
	std::cin.tie(0);
	std::cout.tie(0);
	std::cin>>n>>x;
	if(x==0){
		for(int i=1;i<=n;i++){
			std::cin>>b;
			a[i]=b%mod;
			if(a[i]==0) res=i;
			ans+=res;
		}
	}
	else{
		std::map<int,int>mp;
		res=mp[x]=1;
		for(int i=1;i<=n;i++){
			std::cin>>b;
			a[i]=b%mod;
			if(a[i]==0){
				mp.clear();
				res=mp[x]=1;
			}
			else{
				res=res*a[i]%mod;
				ans+=mp[res];
				++mp[res*x%mod];
			}
		}
	}
	std::cout<<ans<<'\n';
	return 0;
}

os：学习的师哥队的代码，我还是在某些处理上需要加强啊

J - Football Match（计算几何）

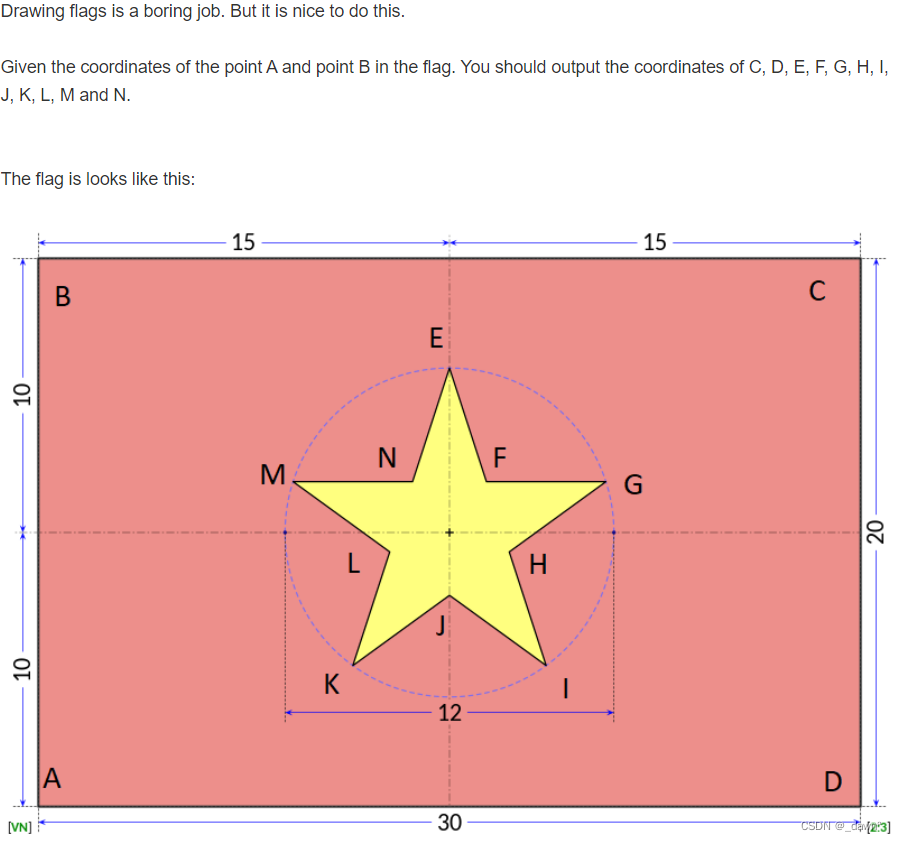
 给出一面旗子的比例，给出A,B两点的坐标，求旗子其他所有点的坐标。

 os：这个题真的是无语，纸质题面和牛客上不一样，，纸质的没有说这个旗子可以旋转，，白费了我们那么长时间，，好叭也是我们不自量力了才会开计算几何题，寄

思路：根据比例计算线段的长度，可以得到点的坐标。对于这个题而言，我们大可以使用原题给的数据按比例缩放后旋转。思路不难，但是非常麻烦。

注：对于关于某点旋转，可以采用矩阵旋转直接带入：

矩阵右乘（x，y）的转置矩阵即可。实际上，我们可以发现，不必考虑顺时针或者逆时针旋转，直接代数，根据角度的正负即可。 

AC Code：

#include <bits/stdc++.h>
 
#define INF 0x3f3f3f3f
typedef long long ll;
typedef long double ld;
const double PI=acos(-1);
int t;
ld xa,ya,xb,yb;
ld xx[]={
	30.000000,30.000000,15.000000,16.347084,20.706339,17.179628,18.526712,15.000000,11.473288,12.820372,9.293661,13.652916
};
ld yy[]={
	20.000000,0.000000,16.000000,11.854102,11.854102,9.291796,5.145898,7.708204,5.145898,9.291796,11.854102,11.854102
};
 
void init(){
	ld MN=(6*sin(PI*2/5))/(1+sin(PI/10));
	ld PF=MN*sin(PI/10);
	ld OP=6*cos(PI*2/5);
	ld PG=6*sin(PI*2/5);
	ld OF=sqrt(PF*PF+OP*OP);
	//F
	xx[3]=15+PF;
	yy[3]=10+OP;
	//G
	xx[4]=15+PG;
	yy[4]=10+OP;
	//H
	xx[5]=15+OF*cos(PI/10);
	yy[5]=10-OF*sin(PI/10);
	//I
	xx[6]=15+6*sin(PI/5);
	yy[6]=10-6*cos(PI/5);
	//J
	yy[7]=10-OF;
	//K
	xx[8]=15-6*sin(PI/5);
	yy[8]=10-6*cos(PI/5);
	//L
	xx[9]=15-OF*cos(PI/10);
	yy[9]=10-OF*sin(PI/10);
	//M
	xx[10]=15-PG;
	yy[10]=10+OP;
	//N
	xx[11]=15-PF;
	yy[11]=10+OP;
}
 
int main(){
	init();
	scanf("%d",&t);
	while(t--){
		scanf("%Lf%Lf%Lf%Lf",&xa,&ya,&xb,&yb);
		xb-=xa,yb-=ya;
		ld sinn=xb,coss=yb;
		for(int i=0;i<12;i++){
			ld sinx=xx[i];
			ld cosx=yy[i];
			ld cosp=cosx*coss-sinx*sinn;
			ld sinp=sinx*coss+cosx*sinn;
			ld ansx=sinp/20+xa;
			ld ansy=cosp/20+ya;
			printf("%.10Lf %.10Lf%c",ansx,ansy,i==11?'\n':' ');
		}
	}
	return 0;
}

os：学习的wygg队的代码，简洁而且很清楚，tqllllll！！！

先这样吧，能力有限，明年省赛再战！

若有错误请指教，谢谢！