-
如何通俗理解海涅定理
如何通俗地解释海涅定理
同学们大家好,今天我们来学习海涅定理。
定理(海涅定理). 对函数
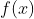 定义域内的任意,且满足
定义域内的任意,且满足 ,
, 的数列
的数列 ,有:
,有:
1 简述
我们知道,极限分为函数极限与数列极限

那么函数极限可以转换为数列极限吗?数列极限可以转换为函数极限吗?

在一定条件下是可以的,海涅定理干的就是这个事。首先来看函数极限转换为数列极限的情况。
2 函数极限转换为数列极限
假设函数在
 处的极限为
处的极限为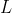

下面在函数定义域内取一数列,令这个数列的极限为

由此数列的函数值组成一个新的数列,这个数列的极限就是
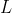
为了看得更清楚一点,我们再建立一个坐标系,左边这个坐标系观察函数极限,横坐标是
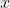 ,纵坐标是
,纵坐标是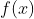 ,右边这个坐标系观察数列极限,横坐标是
,右边这个坐标系观察数列极限,横坐标是 ,纵坐标是
,纵坐标是 ,这里的
,这里的 就是靠近
就是靠近 的那个数列
的那个数列这个数列从左到右排列,可以看到,当
 不断增大时,
不断增大时, 不断靠近靠近一个值,这个值就是
不断靠近靠近一个值,这个值就是 的极限值
的极限值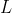
也就是说,若函数在
 处的极限为
处的极限为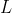 ,且
,且 是极限为
是极限为 的数列,则数列
的数列,则数列 的极限也为
的极限也为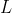

这样我们就从函数极限推出了数列极限
3 数列极限转换为函数极限
还是把目光锁定在有函数曲线这幅图上,这个时候我们只有函数图像,而并不知道其在
 处的极限
处的极限
在定义域内取一数列,使其极限为
 ,并求出其函数值,可以看到这个数列的极限是
,并求出其函数值,可以看到这个数列的极限是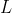
再在定义域内取一极限为
 的数列,可以看到,由它的函数值构成的数列的极限还是
的数列,可以看到,由它的函数值构成的数列的极限还是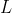
若在定义域内,任取一个极限为
 的数列,它的函数值极限都是
的数列,它的函数值极限都是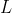 的话,那么函数在
的话,那么函数在 处的极限就为
处的极限就为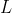
为了将数列极限看得更清楚,这里还是建立一个
 的坐标系
的坐标系
先看蓝色这个数列,这个数列前面讲过了,是从左到右排列的。这里可以很明显的看出,此数列极限为
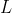 。
。然后看红色数列,红色数列是从右到左排列的。可以看到,当
 趋于无穷时,
趋于无穷时, 的极限也为
的极限也为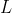
最后来看黄色这个数列,这个数列是交错排列的,可以看到,当
 趋于无穷时,数列
趋于无穷时,数列 的极限还是
的极限还是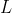
也就是说,若任意一个数列
 ,它的极限都为
,它的极限都为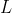 。那么函数在
。那么函数在 处的极限就为
处的极限就为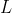 。
。
4 总结
综合前面两节的内容,我们就完成了函数极限与数列极限的互相转换,这就是海涅定理的内容

需要说明的是,海涅定理证明的是一个充要条件。也就是说,如果左边极限不存在,那么右边极限也不存在。反过来,如果右边极限不存在,左边极限也不存在。在实际应用中,我们经常利用这一点。下面来看一道例题。
5 例题
求

5.1 思路
如果我们有做图软件,可以看到函数图像长这样,
 就是白点那个位置。下面我们利用海涅定理,将这个函数极限问题转换为数列极限问题来解决
就是白点那个位置。下面我们利用海涅定理,将这个函数极限问题转换为数列极限问题来解决
因为要求的极限的位置是0,所以我们首先在定义域内找出极限为0的数列,并求出其函数值
接着,我们再在定义域内找出一个极限为0的数列,并求出其函数值
可以很明显地看到,黄色数列和红色数列的极限不一致,因此函数在0点的极限不存在

最后,我们写出证明过程
5.2 证明
(1)

(2)

(3)由于
 均为极限为0的数列,且
均为极限为0的数列,且
由海涅定理可得

-
相关阅读:
java中spark数据集字段下划线改成驼峰
【白话前端】和three.js功能相近的8个js库
Redis使用ZSET实现消息队列使用总结二
python unittest以及coverage report
pytorch【output.topk】用法
9.4 链表删除指定节点(静态创建链表)
Mysql80服务无法启动请输入Net helpMsg3534以获得更多的帮助
AI图像渲染
Spring Cloud Alibaba入门篇
git pull 报错: 在签出前,请清理存储库工作树
- 原文地址:https://blog.csdn.net/ccnt_2012/article/details/125375283