从入门开始手把手搭建千万级Java算法测试-快速排序与随机快速排序比较

  第六天开始呢，我们讲解快速排序与随机快速排序，从算法思路，到算法伪代码实现，到复杂度分析，从这里开始我们手把手搭建一个测试平台的基础，根据你自身硬件水平可以对下列代码进行从1000，到千万级测试，其中算法测试时间与你的机器硬件水平和实现的算法有关系，下面是快速排序与随机快速排序算法的具体讲解。
（1）排序算法的思路并且举例说明
  快速排序基本思想：选择一个基准数，通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小。然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以达到全部数据变成有序。

例如： 8 3 7 4 6 1 2
第一次排序： 2 3 7 4 6 1 8
第二次排序： 1 2 7 4 6 3 8
第三次排序： 1 2 7 4 6 3 8
第四次排序： 1 2 3 4 6 7 8

（2）算法伪代码

//快速排序：
QuickSort(A,left,right):{
   if right<left:
      return   
   m <- Partition(A,left,right)
   QuickSort(A,left, m-1)
   QuickSort(A,m+1,right)
}
Change(A,left,right):{//使用固定位置数
   x <- A[left]
   lower_bound <- left
   greater_bound <- right
   for i from left+1 to right:
      if A[i] <= A[left]:
          swap(A[lower_bound+1],A[i])
          lower_bound <- i+1
   swap(A[lower_bound],A[left])
}
//随机化快速排序：
QuickSort(A,left,right):{
   if right<left:
      return   
   m <- Partition(A,left,right)
   QuickSort(A,left, m-1)
   QuickSort(A,m+1,right)
}
Change(A,left,right):{
   x <- A[left]
   lower_bound <- left
   greater_bound <- right
	j<-  randomNum >=left//使用随机数
   for i from j -1to right:
      if A[i] <= A[left]:
          swap(A[lower_bound+1],A[i])
          lower_bound <- i+1
   swap(A[lower_bound],A[left])
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

（3）复杂度分析
1.快速排序:
  在最优情况下，在上面的change函数中每次都划分得很均匀，如果排序n个关键字,其递归树的深度就为.log2n.+1（.x.表示不大于x的最大整数），即仅需递归log2n次，需要时间为T（n）的话
  第一次change函数应该是需要对整个数组扫描一遍，做n次比较。然后，获得的枢轴将数组一分为二，那么各自还需要T（n/2）的时间（注意是最好情况，所以平分两半）。
  于是不断地划分下去，我们就有了下面的不等式推断。
T（n）≤2T（n/2） +n，T（1）=0
T（n）≤2（2T（n/4）+n/2） +n=4T（n/4）+2n
T（n）≤4（2T（n/8）+n/4） +2n=8T（n/8）+3n
……
T（n）≤nT（1）+（log2n）×n= O(nlogn)
由数学归纳法可证明，其数量级为O(nlogn)。（编者也可以尝试主定理法）
  空间复杂度来说，主要是递归造成的栈空间的使用，最好情况，递归树的深度为log2n，其空间复杂度也就为O(logn)，最坏情况，需要进行n‐1递归调用，其空间复杂度为O(n)，平均情况，空间复杂度也为O(logn)
由于关键字的比较和交换是跳跃进行的，因此，快速排序是一种不稳定的排序方法。

平均时间复杂度：O(nlog2n)
最好时间复杂度：O(nlog2n)(枢纽元选取得当，每次都能均匀的划分序列)
最差时间复杂度：O(n2) (枢纽元为最大或者最小数字)
空间复杂度：O(n)
稳定性：不稳定

2.随机快速排序：
  运行时间不依赖于输入的排序情况,最坏情况仅由随机数的生成决定,所以只是提高了算法的稳定性，对整体的时间复杂度和空间复杂度没有影响。

（4）代码主体部分

package runoob;
import java.util.Arrays;

public class Quick_sort {
    public static void sort(Integer[] arr, int L, int R) {
        //边界条件是只有一个元素的时候退出也就是左边等于右边
        if (L >= R) {
            return;
        }//nextlow指向即将填充比pivot小的值得位置
        long pivot = arr[L];
        int nextLow = L + 1;
        int now = L + 1;//小于等于是因为不排除相同的情况
        while (now <= R) {
            if (arr[now] <= pivot) {
                swap(arr, now, nextLow);
                nextLow++;
                now++;
            } else {
                now++;
            }
        }
        swap(arr, L, nextLow - 1);
        sort(arr, L, nextLow - 1 - 1);
        sort(arr, nextLow, R);
    }
    public static void RondamQuickSort(Integer[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        Process(arr, 0, arr.length - 1);
    }
    public static void swap(Integer[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
        public static void Process(Integer[] arr, int L, int R) {
            if (L >= R) {
                return;
            }
            swap(arr, L + (int) (Math.random() * (R - L + 1)), R);
            Integer[] equalArea = Nether_lands(arr, L, R);
            Process(arr, L, equalArea[0] - 1);
            Process(arr, equalArea[1] + 1, R);
        }
        public static Integer[] Nether_lands(Integer[] arr, int L, int R) {
            if (L > R) {
                return new Integer[]{-1, -1};
            }
            if (L == R) {
                return new Integer[]{L, R};
            }
            int less = L - 1;
            int more = R;
            int index = L;
            while (index < more) {
                if (arr[index].equals(arr[R])) {
                    index++;
                } else if (arr[index] < arr[R]) {
                    swap(arr, index++, ++less);
                } else {
                    swap(arr, index, --more);
                }
            }
            swap(arr, more, R);
            return new Integer[]{less + 1, more};
        }
    public static void Quicksort_text(long num) {
        Integer[] arr = SortHelper.generateRandomArray(num, 0, 100);//使用数的范围1-100
        Integer[] arr2 = Arrays.copyOfRange(arr, 0, arr.length - 1);

        long start = System.nanoTime();
        sort(arr, 0, arr.length - 1);
        long mid = System.nanoTime();
        RondamQuickSort(arr2);
        long end = System.nanoTime();

        System.out.println("当前数据数量为"+num+"为了页面干净选择忽略打印排序结果");
        System.out.println("快速排序"+"花费时间:" + (mid - start)/1000 + "(ms)");
        System.out.println("随机快速排序"+"花费时间:" + (end - mid)/1000 + "(ms)");
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82

  对应代码中的SortHelper类我们留一个小小的悬念，留到最后来进行叙说，其中目前来说他的方法generateRandomArray的参数为，（num，left，right）第一个参数参与算法生成的数量级，作为随机生成序列，它可以为千万，因为是long级别，left和right则为生成序列的大小范围，生成的序列为返回值类型为Integer[]。
（5）测试结果如下：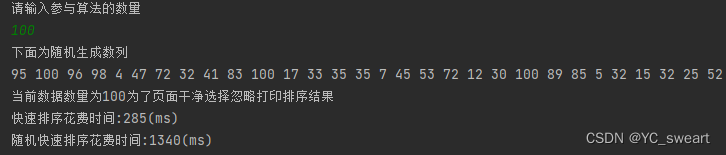

  笔者有兴趣可以尝试千万级的算法测试，这里便不在赘述。