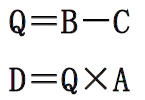向量处理机简介

向量由一组有序、具有相同类型和位数的元素组成。

在流水线处理机中，设置了向量数据表示和相应的向量指令的，称为向量处理机。

不具有向量数据表示和相应的向量指令的流水线处理机，称为标量处理机

典型的向量处理机:

• 1976年Cray-1超级计算机浮点运算速度达到了每秒1亿次
• CDC Cyber 205，Cray Y-MP，NEC SX-X/44，Fujitsu VP2600等性能达到了每秒几十亿～几百亿次浮点运算

4.1 向量的处理方式 🌟

//以计算表达式D=A×（B－C）为例
A、B、C、D── 长度为N 的向量
main()
{   // 设A、B、C、D都是长度为n的数组
    for(int i=0;i<n;i++)
    {
        D[i]=A[i]*(B[i]-C[i]);
    }
}
1
2
3
4
5
6
7
8
9

横向(水平)处理方式

• 向量计算是按行的方式从左到右横向的进行的
  • 
• 组成循环程序进行处理
  • 
• 这样以来:
  • 有数据相关N次
  • 功能切换(也就是加法和乘法功能切换):2N次
• 所以,该种方法并不适合向量处理机的并行处理模式

纵向(垂直)处理方式🌟🌟

• 向量计算是按列的方式从上到下纵向的进行
• 
• 表示成向量指令为:
  • 
• 这样以来:
  • 没有数据相关
  • 功能切换仅仅1次

纵横(分组)处理方式🌟🌟

• 把向量分成若干组,组内按纵向方式处理,依次处理各组
• 
• 计算过程为:
  • 
  • 

4.2 向量处理机的结构

向量处理机的结构因具体机器不同而不同。

由所采用的向量处理方式决定。

有两种典型的结构

4.2.1 存储器-存储器型结构(纵向处理方式采用)

• 采用纵向处理方式的向量处理机对处理机结构的要求：存储器－存储器结构

  • 向量指令的源向量和目的向量都是存放在存储器中，运算的中间结果需要送回存储器。
  • 流水线运算部件的输入和输出端都直接（或经过缓冲器）与存储器相联，从而构成存储器-存储器型操作的运算流水线。
  • 举例:STAR-100、CYBER-205

• “存储器－存储器”型操作的运算流水线

  • 

• 要充分发挥这种结构的流水线效率，存储器要不断地提供源操作数，并不断地从运算部件接收结果。

  • 每拍从存储器读取两个数据，并向存储器写回一个结果）
  • 对存储器的带宽以及存储器与处理部件的通信带宽提出了非常高的要求。
  • 解决方法：一般是通过采用多体交叉并行存储器和缓冲器技术。
    • 

4.2.2 寄存器-寄存器型结构(分组处理方式采用)

• 在向量的分组处理方式中，对向量长度N没有限制，但组的长度n却是固定不变的。
  • 对处理机结构的要求：寄存器－寄存器结构
  • 设置能快速访问的向量寄存器，用于存放源向量、目的向量及中间结果。让运算部件的输入、输出端都与向量寄存器相联，就构成了“寄存器－寄存器”型操作的运算流水线。
  • 典型的寄存器－寄存器结构的向量处理机:美国的CRAY-1、我国的YH-1巨型机
• 以CRAY-1为例进行分析:
  • 基本结构
    • 功能部件:共有12条可并行工作的单功能流水线，可分别流水地进行地址、向量、标量的各种运算。
    • 
    • 6个单功能流水部件：进行向量运算
      • 
      • 括号中的数字为其流水经过的时间，每拍为一个时钟周期，即12.5ns。
    • 向量寄存组V
      • 
    • 标量寄存器S和快速暂存器T
      • 
    • 向量屏蔽寄存器VM
      • 
  • CRAY-1向量处理的一个显著特点
    • 每个向量寄存器Vi都有连到6个向量功能部件的单独总线。
    • 每个向量功能部件也都有把运算结果送回向量寄存器组的总线。
    • 只要不出现Vi冲突和功能部件冲突，各Vi之间和各功能部件之间都能并行工作，大大加快了向量指令的处理。
      • Vi冲突：并行工作的各向量指令的源向量或结果向量使用了相同的Vi。
        • 
      • 功能部件冲突：并行工作的各向量指令要使用同一个功能部件。

4.3 提高向量处理机性能的常用技术

提高向量处理机性能的方法

设置多个功能部件，使它们并行工作；

设置多个独立的功能部件。这些部件能并行工作，并各自按流水方式工作，从而形成了多条并行工作的运算操作流水线

采用链接技术，加快一串向量指令的执行；

• 两条向量指令占用功能流水线和向量寄存器的4种情况
  1. 指令不相关
  2. 功能部件冲突
  3. 源寄存器冲突
  4. 结果寄存器冲突
• 当前一条指令的结果寄存器是后一条指令的源寄存器、且不存在任何其他冲突时，就可以用链接技术来提高性能。
  • 
  • **向量流水线链接：**具有先写后读相关的两条指令，在不出现功能部件冲突和源向量冲突的情况下，可以把功能部件链接起来进行流水处理，以达到加快执行的目的。
  • 
  • 由于同步的需求，链接时，Cray-1中把向量数据元素送往向量功能部件以及把结果存入向量寄存器都需要一拍时间，从存储器中把数据送入访存功能部件也需要一拍时间。
• 进行向量链接的要求
  • 保证：无向量寄存器使用冲突和无功能部件使用冲突
  • 只有在前一条指令的第一个结果元素送入结果向量寄存器的那一个时钟周期才可以进行链接。
  • 当一条向量指令的两个源操作数分别是两条先行指令的结果寄存器时，要求先行的两条指令产生运算结果的时间必须相等，即要求有关功能部件的通过时间相等。
  • 要进行链接执行的向量指令的向量长度必须相等，否则无法进行链接。

采用分段开采技术，加快循环处理；

处理向量的长度大于向量寄存器的长度的情况

当向量的长度大于向量寄存器的长度时，必须把长向量分成长度固定的段，然后循环分段处理，每一次循环只处理一个向量段。这种技术称为分段开采技术。

由系统硬件和软件控制完成，对程序员是透明的

采用多处理机系统，进一步提高性能。

4.4 向量处理机的性能评价

向量指令的处理时间$T_{vp}$

• 一条向量指令的处理时间$T_{vp}$

  • 执行一条向量长度为 n 的向量指令所需的时间为:
    $$T_{vp}=T_s+T_e+(n-1)T_c$$

    $T_{s} $ : 向量处理部件流水线的建立时间为了使处理部件流水线能开始工作（即开始流入数 据）所需要的准备时间。
    $T_e$ : 向量流水线的通过时间第一对向量元素通过流水线并产生第一个结果所花的时间。
    $T_c$ : 流水线的时钟周期时间

  • 把上式中的参数都折算成时钟周期个数：

    $$T_{vp}=[s+e+(n-1)]T_c$$

    s: $T_s$ 所对应的时钟周期数
    e: $\mathbf{T}{\mathrm{e}} $ 所对应的时钟周期数不考虑 $T_s$,并令 $ T{\text {start }}=e-1 $

    $$T_{vp}=\left(T_{start}+n\right)T_c$$

    $ \mathrm{T}_{\text {start }} $ ：从一条向量指令开始执行到还差一个时钟周期就产生第一个结果所需的时钟周期数。可称之为 该向量指令的启动时间 。此后, 便是每个时钟周期 流出一个结果, 共有 $ \mathrm{n} $个结果。

• 一组向量指令的处理时间

  • 对于一组向量指令而言，其执行时间主要取决于三个因素：

    • 向量的长度
    • 向量操作之间是否存在流水功能部件的使用冲突
    • 数据的相关性

  • 把能在同一个时钟周期内一起开始执行的几条向量指令称为一个编队。

    • 可以看出：同一个编队中的向量指令之间一定不存在流水向量功能部件的冲突和数据的冲突。

  • 编队后，这个向量指令序列的总的执行时间为各编队的执行时间的和。
    $$T_{all}=\sum _{i=1}^m{T}_{vp}^{(i)}$$

    ${\mathrm{T}}^{(\mathrm{i})}\mathrm{v}\mathrm{p}$ : 第 $\mathrm{i}$ 个编队的执行时间
    $\mathrm{m}$ ：编队的个数

  • 当一个编队是由若干条指令组成时，其执行时间就应该由该编队中各指令的执行时间的 最大值 来确定。

    • $T(i){}_{\text{start }}$ ：第i编队中各指令的启动时间的最大值

    • $$T_{\text{all }}=\sum _{i=1}^m{T}_{vp}^{(i)}=\sum _{i=1}^m\left(T_{\text{start }}^{(i)}+n\right)T_c=\left(\sum _{i=1}^m{T}_{\text{start }}^{(i)}+mn\right)T_c=\left(T_{\text{start }}+mn\right)T_c$$

    • $T_{\text {start }}=\sum_{i=1}^{m} T_{\text {start }}^{(i)} $该组指令总的启动时间（时钟周期个数）

    • 表示成时钟周期个数
      $${\mathrm{T}}_{\text{all }}={\mathrm{T}}_{\text{start }}+\mathbf{m}\mathbf{n}$$

• 分段开采时,一组向量指令的总执行时间

  • 当向量长度n大于向量寄存器长度MVL时，需要分段开采。

  • 引入一些客外的处理操作(假设: 这些操作所引入的额外时间为 ${\mathrm{T}}_{\text{loop }}$ 个时钟周期) 口 设 $ \left[\frac{n}{M V L}\right\rfloor=p $ $\quad \mathrm{q} $ ： 余数
    共有 $\mathbf{m} $个编队
    对于最后一次循环来说, 所需要的时间为:
    $${\mathrm{T}}_{\text{last }}={\mathrm{T}}_{\text{start }}+{\mathrm{T}}_{\text{loop }}+\mathbf{m}\times \mathbf{q}$$

  • 其他的每一次循环所要花费的时间为:
    $$T_{\text{step }}=T_{\text{start }}+T_{\text{loop }}+m\times MVL$$

    总的执行时间为:
    T all  = T step  × p + T last  = ( T start  + T loop  + m × M V L ) × p + ( T start  + T loop  + m × q ) = ( p + 1 ) × ( T start  + T loop  ) + m ( M V L × p + q ) = [ n M V L ] × ( T start  + T loop  ) + m n

    Tall =Tstep ×p+Tlast =(Tstart +Tloop +m×MVL)×p+(Tstart +Tloop +m×q)=(p+1)×(Tstart +Tloop )+m(MVL×p+q)=[nMVL]×(Tstart +Tloop )+mn$$\begin{array}{rl}{\mathrm{T}}_{\text{all }}& ={\mathrm{T}}_{\text{step }}\times \mathrm{p}+{\mathrm{T}}_{\text{last }}\\ & =\left({\mathbf{T}}_{\text{start }}+{\mathbf{T}}_{\text{loop }}+\mathbf{m}\times \mathbf{M}\mathbf{V}\mathbf{L}\right)\times \mathbf{p}+\left({\mathbf{T}}_{\text{start }}+{\mathbf{T}}_{\text{loop }}+\mathbf{m}\times \mathbf{q}\right)\\ & =(\mathbf{p}+\mathbf{1})\times \left({\mathbf{T}}_{\text{start }}+{\mathbf{T}}_{\text{loop }}\right)+\mathbf{m}(\mathbf{M}\mathbf{V}\mathbf{L}\times \mathbf{p}+\mathbf{q})\\ & =\left[\frac{n}{MVL}\right]\times \left(T_{\text{start }}+T_{\text{loop }}\right)+mn\end{array}$$
    Tall ​​=Tstep ​×p+Tlast ​=(Tstart ​+Tloop ​+m×MVL)×p+(Tstart ​+Tloop ​+m×q)=(p+1)×(Tstart ​+Tloop ​)+m(MVL×p+q)=[MVLn​]×(Tstart ​+Tloop ​)+mn​

最大性能${\mathrm{R}}_{\infty }$ 和半性能向量长度 ${\mathrm{n}}_{1/2}$

• 向量处理机的峰值性能 $R_{\infty }$
  $R_{\infty} $ 表示当向量长度为无穷大时, 向量处理机的 最高性能, 也称为峰值性能。
  $$R_{\infty }=\underset{n\to \infty }{\lim }\frac{\text{ 向量指令序列中浮点运算次数 }\times \text{ 时钟频率 }}{\text{ 向量指令序列执行所需的时钟周期数 }}$$

• 半性能向量长度${\mathrm{n}}_{1/2}$

  • 半性能向量长度$n_{1/2}$是指向量处理机的性能为其最大性能的一半时所需的向量长度。
  • 评价向量流水线的建立时间对性能影响的重要参数。

向量长度临界值$n_v$

• 向量长度临界值$n_v$是指：对于某一计算任务而言，向量方式的处理速度优于标量串行方式处理速度时所需的最小向量长度。