经典问题
题目描述
- 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
- 提示:
- 链表中节点的数目范围是 [0, 5000]。
- -5000 <= Node.val <= 5000。
举个栗子
- 示例 1:
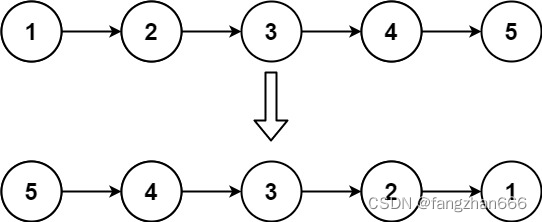
- 输入:head = [1,2,3,4,5]。
- 输出:[5,4,3,2,1]。
- 示例 2:
- 输入:head = [1,2]。
- 输出:[2,1]。

- 示例 3:
解题思路
- 双指针迭代
- 申请两个指针,第一个指针叫 pre,最初是指向 null 的。
- 第二个指针 cur 指向 head,然后不断遍历 cur。
- 每次迭代到 cur,都将 cur 的 next 指向 pre,然后 pre 和 cur 前进一位。
- 都迭代完了(cur 变成 null 了),pre 就是最后一个节点了。
- 递归解法
- 递归解法就是先假设 head 节点之外的节点都已经反转成功了,那么 head 节点反转(head.next.next = head)则是递归的基本条件。
- 递归的两个条件:
- 终止条件是当前节点或者下一个节点==null。
- 在函数内部,改变节点的指向,也就是 head 的下一个节点指向 head。
代码来了
class Solution {
public ListNode reverseList(ListNode head) {
ListNode pre = null;
ListNode cur = head;
while (cur != null) {
ListNode tmp = cur.next;
cur.next = pre;
pre = cur;
cur = tmp;
}
return pre;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
class Solution {
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
ListNode cur = reverseList(head.next);
head.next.next = head;
head.next = null;
return cur;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
题目描述
- 给你一个链表的头节点 head 和一个整数 val,请你删除链表中所有满足 Node.val == val 的节点,并返回新的头节点。
- 提示:
- 列表中的节点数目在范围 [0, 104] 内。
- 1 <= Node.val <= 50。
- 0 <= val <= 50。
举个栗子
- 示例 1:
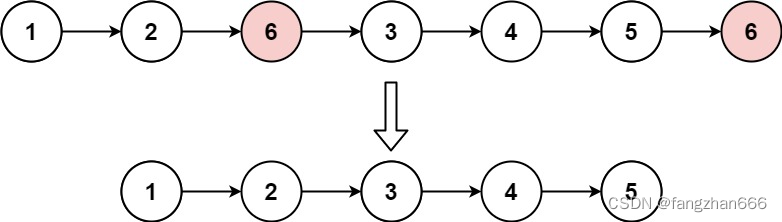
- 输入:head = [1,2,6,3,4,5,6], val = 6。
- 输出:[1,2,3,4,5]。
- 示例 2:
- 输入:head = [], val = 1。
- 输出:[]。
- 示例 3:
- 输入:head = [7,7,7,7], val = 7。
- 输出:[]。
代码来了
class Solution {
public ListNode removeElements(ListNode head, int val) {
ListNode dummy = new ListNode(val - 1);
dummy.next = head;
ListNode cur = dummy;
while (cur.next != null) {
if (cur.next.val == val) {
cur.next = cur.next.next;
}else {
cur = cur.next;
}
}
return dummy.next;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
题目描述
- 给定单链表的头节点 head ,将所有索引为奇数的节点和索引为偶数的节点分别组合在一起,然后返回重新排序的列表。
- 第一个节点的索引被认为是奇数, 第二个节点的索引为偶数,以此类推。
- 请注意,偶数组和奇数组内部的相对顺序应该与输入时保持一致。
- 你必须在 O(1) 的额外空间复杂度和 O(n) 的时间复杂度下解决这个问题。
- 提示:
- n == 链表中的节点数。
-
0
<
=
n
<
=
1
0
4
0 <= n <= 10^4
0<=n<=104。
-
−
1
0
6
<
=
N
o
d
e
.
v
a
l
<
=
1
0
6
-10^6 <= Node.val <= 10^6
−106<=Node.val<=106。
举个栗子
- 示例 1:
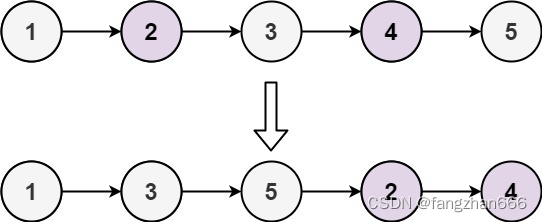
- 输入: head = [1,2,3,4,5]。
- 输出: [1,3,5,2,4]。
- 示例 2:
- 输入: head = [2,1,3,5,6,4,7]。
- 输出: [2,3,6,7,1,5,4]。

解题思路
- 如果链表为空,则直接返回链表。
- 对于原始链表,每个节点都是奇数节点或偶数节点。
- 头节点是奇数节点,头节点的后一个节点是偶数节点,相邻节点的奇偶性不同。
- 因此可以将奇数节点和偶数节点分离成奇数链表和偶数链表,然后将偶数链表连接在奇数链表之后,合并后的链表即为结果链表。
- 原始链表的头节点 head 也是奇数链表的头节点以及结果链表的头节点,head 的后一个节点是偶数链表的头节点。
- 令 evenHead = head.next,则 evenHead 是偶数链表的头节点。
- 维护两个指针 odd 和 even 分别指向奇数节点和偶数节点,初始时 odd = head,even = evenHead。
- 通过迭代的方式将奇数节点和偶数节点分离成两个链表,每一步首先更新奇数节点,然后更新偶数节点。
- 更新奇数节点时,奇数节点的后一个节点需要指向偶数节点的后一个节点,因此令 odd.next = even.next,然后令 odd = odd.next,此时 odd 变成 even 的后一个节点。
- 更新偶数节点时,偶数节点的后一个节点需要指向奇数节点的后一个节点,因此令 even.next = odd.next,然后令 even = even.next,此时 even 变成 odd 的后一个节点。
- 全部节点分离完毕的条件是 even 为空节点或者 even.next 为空节点,此时 odd 指向最后一个奇数节点(即奇数链表的最后一个节点)。
- 最后令 odd.next = evenHead,将偶数链表连接在奇数链表之后,即完成了奇数链表和偶数链表的合并,结果链表的头节点仍然是 head。
代码来了
class Solution {
public ListNode oddEvenList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
ListNode oddDummy = new ListNode(0);
ListNode evenDummy = new ListNode(0);
oddDummy.next = head;
evenDummy.next = head.next;
ListNode curOdd = head;
ListNode curEven = head.next;
while(curEven != null && curEven.next != null) {
curOdd.next = curEven.next;
curOdd =curOdd.next;
curEven.next = curOdd.next;
curEven = curEven.next;
}
curOdd.next = evenDummy.next;
return oddDummy.next;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
题目描述
- 给你一个单链表的头节点 head,请你判断该链表是否为回文链表。
- 如果是,返回 true;否则,返回 false。
- 提示:
- 链表中节点数目在范围
[
1
,
1
0
5
]
[1, 10^5]
[1,105] 内。
- 0 <= Node.val <= 9。
举个栗子
- 示例 1:
- 输入:head = [1,2,2,1]。
- 输出:true。

- 示例 2:
- 输入:head = [1,2]。
- 输出:false。

解题思路
- 避免使用 O(n) 额外空间的方法就是改变输入。
- 我们可以将链表的后半部分反转(修改链表结构),然后将前半部分和后半部分进行比较。
- 比较完成后我们应该将链表恢复原样。
- 虽然不需要恢复也能通过测试用例,但是使用该函数的人通常不希望链表结构被更改。
- 该方法虽然可以将空间复杂度降到 O(1),但是在并发环境下,该方法也有缺点。在并发环境下,函数运行时需要锁定其他线程或进程对链表的访问,因为在函数执行过程中链表会被修改。
- 整个流程可以分为以下五个步骤:
- 找到前半部分链表的尾节点。
- 反转后半部分链表。
- 判断是否回文。
- 恢复链表。
- 返回结果。
- 使用快慢指针在一次遍历中找到:
- 慢指针一次走一步,快指针一次走两步,快慢指针同时出发。
- 当快指针移动到链表的末尾时,慢指针恰好到链表的中间。
- 通过慢指针将链表分为两部分。
- 若链表有奇数个节点,则中间的节点应该看作是前半部分。
代码来了
class Solution {
public boolean isPalindrome(ListNode head) {
if (head == null) {
return true;
}
ListNode firstHalfEnd = endOfFirstHalf(head);
ListNode secondHalfStart = reverseList(firstHalfEnd.next);
ListNode p1 = head;
ListNode p2 = secondHalfStart;
boolean result = true;
while (result && p2 != null) {
if (p2.val != p1.val) {
return false;
}
p1 = p1.next;
p2 = p2.next;
}
firstHalfEnd.next = reverseList(secondHalfStart);
return result;
}
private ListNode reverseList(ListNode head) {
ListNode prev = null;
ListNode curr = head;
while (curr != null) {
ListNode nextTemp = curr.next;
curr.next = prev;
prev = curr;
curr = nextTemp;
}
return prev;
}
private ListNode endOfFirstHalf(ListNode head) {
ListNode fast = head;
ListNode slow = head;
while (fast.next != null && fast.next.next != null) {
fast = fast.next.next;
slow = slow.next;
}
return slow;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65






