算法复杂度是什么？

算法复杂度是什么？

概述

解决问题方法的效率，与算法的巧妙程度和所占的空间大小是有关系的。算法笨拙，消耗的时间就相对较多；空间占用过高，可能导致程序最终没有结果就已经崩溃。

复杂度

空间复杂度S(n)——根据算法写成的程序在执行时占用存储单元的长度。

时间复杂度T(n)——根据算法写成的程序在执行时消耗时间的长度。

复杂度的渐进表示法

为什么我们常看到的复杂度表示是O(n)，这就是复杂度的渐进表示法

O(n)        表示复杂度的最小是上界

Ω(n) 表示复杂度的最大下界

Θ(n) 表示既是复杂度的上界，又是复杂度的下界

常见复杂度量级

函数由上至下，时间复杂度越来越大

作为一个程序员，如果看到一个复杂度是 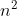$n^{2}$ ，第一个想法就是是否能降成n $\log n$

输入规模n
函数 1 2 4 8 16 32
1 1 1 1 1 1 1
$\log n$ 0 1 2 3 4 5
n 1 2 4 8 16 32
n $\log n$ 0 2 8 24 64 160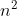
$n^{2}$ 1 4 16 64 256 1024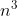
$n^{3}$ 1 8 64 512 4096 32768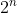
$2^{n}$ 2 4 16 256 65536 4.29* 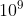$10^{9}$
n! 1 2 24 40326 2.09* $10^{12}$ 2.6* $10^{37}$

复杂度分析窍门

如果有两段算法，我们知道两端算法的复杂度上界是O(f1(n))、O(f2(n))

        当把这两个算法没有嵌套时，复杂度是max(O(f1(n)),O(f2(n)))

        当两个算法有嵌套时，复杂度是O(f1(n)*f2(n))

一个for循环的时间复杂度=循环次数*循环体代码复杂度

if else结构的复杂度，取决于if的条件复杂度、两个分支的复杂度，三者中复杂度最大的。
相关阅读:
2023年中国商业版服务器操作系统市场发展规模分析：未来将保持稳定增长[图]
什么是希尔排序？
424. 替换后的最长重复字符 ●●
MySQL8高级
 成都优优聚是专业美团代运营吗？
基于Qlearning强化学习的机器人路线规划仿真
 python发送企业微信群webhook消息（文本、文件）
【C++编程】类的静态 static 成员 & 常 const 函数
 企业电子招标采购系统源码Spring Boot + Mybatis + Redis + Layui + 前后端分离构建企业电子招采平台之立项流程图
 基于Android的仓库管理系统APP设计与实现
原文地址：https://blog.csdn.net/qq522044637/article/details/125417173

	输入规模n
函数	1	2	4	8	16	32
1	1	1	1	1	1	1
$\log n$	0	1	2	3	4	5
n	1	2	4	8	16	32
n $\log n$	0	2	8	24	64	160
$n^{2}$	1	4	16	64	256	1024
$n^{3}$	1	8	64	512	4096	32768
$2^{n}$	2	4	16	256	65536	4.29* $10^{9}$
n!	1	2	24	40326	2.09* $10^{12}$	2.6* $10^{37}$

概述

复杂度

复杂度的渐进表示法

常见复杂度量级

复杂度分析窍门