Improved Security for a Ring-Based Fully Homomorphic Encryption Scheme-2013：解读

本文记录阅读此论文的笔记

摘要#

（1）1996年，HPS三人提出一个格上的高效加密方案，叫做NTRUEncrypt，但是没有安全性证明；之后2011年，SS等人修改此方案，将其安全规约到标准格上的困难问题；2012年，LTV等人基于修改的方案，提出一个FHE方案。

（2）non-standard assumption：非标准假设，是什么意思？

（3）本片论文是去除了non-standard assumption，通过使用**技术，并且构建了一个新的FHE方案，基于标准格假设问题（比如，SVP，CVP等）和循环安全假设【circular security assumption】。

（4）scale-invariant：缩放比例不变？

（5）该方案不使用模切换【modulus switching】，且密文是一个环元素（在环上）；另外给出一个实用的变体方案，其具有强假设，并给出推荐的参数和性能提升后的结果。

（6）最后，给出了一种优化方法，可以扩展密文大小，利用CRT技术。

介绍#

（1）【On-the-fly multiparty compu- tation on the cloud via multikey fully homomorphic encryption-2012】提出一个多密钥的FHE方案，是基于【Making NTRU as secure as worst-case problems over ideal lattices-2011】--对【NTRU: A ring-based public key cryp- tosystem-1998】的安全性进行证明。但方案为了保证安全性，需要额外的假设（decisional small polynomial ratio (DSPR) ）。
对应摘要中的（1）

（2）该方案去掉了这个额外的假设；原来的是基于理想格，该方案基于的是格上的标准问题；引入张量技术（tensoring technique）【Fully homomorphic encryption without modulus switching from clas- sical GapSVP】降低噪音

（3）该方案是scale-invariant，即可以不使用模交换技术；该方案中的密文是一个环元素，而一半基于(R)LWE的方案密文都是两个以上的环元素，这能降低密文大小；最后给出一种增加明文空间大小的技术，即通过使用CRT技术，将小的明文模数变为大的明文模数。

（4）参数变大，密文大小变大。

预备知识#

环上的有界分布（B-bounded）#

取自该分布中的元素是有界限的，即无穷范数是小于BB的。

具体的分布：离散高斯分布（discrete Gaussian distribution）

DZ,σDZ,σ：均值为0，方差为σσ，采样概率为exp(−π|x|2/σ2)exp(−π|x|2/σ2)。

通常在FHE中，噪音多项式需要采用该方式采样，选取的元素，值小且概率高。

通过拒绝采样法（rejecting samples），来保证该分布是有界的。

通常多项式的系数在环上，一个数xx需要模qq，有两种表示：x∈(−q/2,q/2)x∈(−q/2,q/2)或者x∈[.]qx∈[.]q；还有一种是x∈[0,q)x∈[0,q)，用rq(x)rq(x)表示xx模qq。

该方案中，使用两种模表示。方案中的qq是密文多项式的系数模数，还有一个确定明文消息空间的明文模数t<qt<q，满足：q−rt(q)=Δ∗tq−rt(q)=Δ∗t，其中Δ=⌊q/t⌋Δ=⌊q/t⌋

下面讲解了BitDecomp和PowersOfTwo两个技术以及其性质：
其中，ww相当于是基，这里取w=2w=2。
（1）BitDecomp
当w=2时，给出一个环上的元素（整数多项式，可以看成一个整数向量（多项式系数））x∈R，变为二进制表示的向量。

例如：q=5，即lw,q=4，(1,2)变为([1,0,0,0],[0,1,0,0])

（2）PowersOfTwo
当w=2时，给出一个环上的元素（整数多项式，可以看成一个整数向量（多项式系数））x∈R，变为元素乘以w的倍数。
例如：q=5，即lw,q=4，(1,2)变为([1,2,4,3],[2,4,3,1])

（3）性质
<BitDecomp(x),PowersOfTwo(y)>=xy(modq)
例如：<([1,0,0,0],[0,1,0,0]),([1,2,4,3],[2,4,3,1])>=1∗1+2∗2(mod5)=5

将环上的元素扩展为多个，进行BitDecomp和PowersOfTwo计算，并且介绍了张量乘（tensor product）。
（1）BitDecomp
当w=2时，给出多个环上的元素（整数多项式，每一个可以看成一个整数向量（多项式系数））x∈Rl，变为二进制表示的向量。

例如：q=5,l=2，即lw,q=4，([1,2],[0,1])变为([1,0,0,0],[0,1,0,0],[0,0,0,0],[1,0,0,0])

（2）PowersOfTwo
当w=2时，给出多个环上的元素（整数多项式，每个可以看成一个整数向量（多项式系数））x∈Rl，变为元素乘以w的倍数。
例如：q=5,l=2，即lw,q=4，([1,2],[0,1])变为([1,2,4,3],[2,4,3,1],[0,0,0,0],[1,2,4,3])

（3）张量乘
(a1,12)⨂(b1,b2)=(a1∗b,a2∗b)=(a1∗b1,a1∗b2,a2∗b1,a2∗b2)
例如：([1,0,0,0,0,1,0,0],[0,0,0,0,1,0,0,0])⨂([1,2,4,3,2,4,3,1],[0,0,0,0,1,2,4,3])=([1,0,0,0,0,4,0,0],[0,0,0,0,0,2,0,0],[0,0,0,0,0,0,0,0],[0,0,0,0,1,0,0,0])

最后说到，在方案计算中，会出现有理数计算（小数），所以最后需要摄入操作化为整数，这里的舍入用的是“四舍五入”。

RLWE问题#

RLWE问题来自【On ideal lattices and learning with errors over rings】。
这里给出的是D-RLWR问题，困难性可以“量子规约”到格理想上的SVP问题

DSPR问题#

DSPR问题：区分h和一个随机采样值是难以区分的。

基础方案#

这部分介绍一个公钥加密方案，基于Regev框架，是下面同态加密方案的基础。

密文模数q，明文模数t∈(1,q)，密文空间为Rq=Zq[x]/Φ(x)，明文空间为Rt=Zt[x]/Φ(x)，密钥和误差取自不同的分布。[m]t表示m mod t。
正确性性：

如果满足以上定理，则可以正确解密。
fc=(tf′+1)(q/t.m+e+hs)=(tf′+1)q/t.m+(tf′+1)(e+hs)(modq)=q/t.m+(...)=Δ.m+v

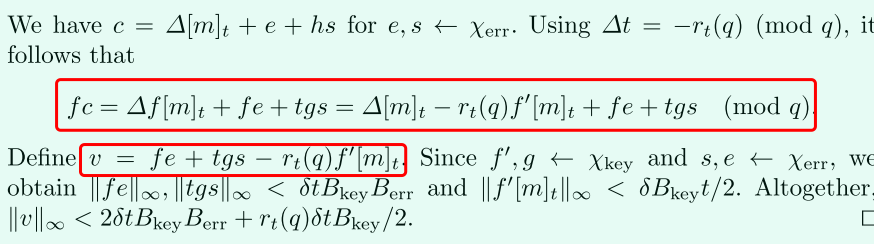
只要v的范数够小，就看可以恢复出明文，所以v也叫做密文c的内在噪音。
下面给出内在噪音v的具体范数范围：

所以能解密成功。

Leveled-FHE方案#

下面基础上面的公钥加密方案，给出一个SWHE方案YASHE，包含同态计算以及分析其计算过程中密文噪音的上限：


可以看到，在乘法后需要进行密钥交换，降低密文维数，加法则不用，因为加法不会导致密文维数变大。
重点在于：计算密钥γ是如何生成的？同态乘法计算后如何降低密文噪音和维数的？

同态加法#

同态加法就是将两个密文直接相加，加完后的噪音小于两个密文的噪音之和+模操作产生的噪音rt(q)，其中rt(q)=qmodt。这里给了相加密文的噪音上限。
这里需要知道：Δt=⌊q/t⌋t=−rt(q)(modq)=−q(modt)(modq)→q(modt)=q−⌊q/t⌋t

同态乘法#

密文乘法分为两步：（1）直接将两密文相乘，获得一个中间密文(对应的明文是[m1.m2]t)，它不能直接使用私钥解密。（2）将其转换为一个可以用私钥解密的新密文，在这里用到了重线性化技术(BV11)/密钥交换技术(BGV)进行密文转换。
噪音处理主要在该步骤。

第一步给出了如何计算中间密文˜cmult，并且分析噪音增长上限，这里可以看出将两个密文先进行PowerOfTwo操作，然后张量乘，维数扩张一倍，所以后面需要降维，同时这步骤也产生了噪音，所以也需要降噪。

第二步给出了密钥交换的过程，以及分析噪音增长的上界。
首先，需要求出用于密钥交换的计算密钥evk，它其实可以看作是f−1P(D(f)⨂D(f))在公钥h下的加密，当然可以用私钥f解密。这里的evk是公开的，所以这里需要做一个“循环安全假设(circular security assumption)”，即即使公开evk，也不会影响方案的安全性。
另外可以看出，这里做密钥交换，也产生了一些噪音。这些噪音通过Decompt和PowerOfTwo技术控制在一定的范围内，增长缓慢。

正确性#

这里给出在解密正确的前提下乘法次数的界限。方案的安全性基于DSPR问题，需要设置好参数。

安全性#

为了证明方案是安全的，需要假设即使敌手知道了evk，方案也可以保证是IND-CPA安全的。
在“循环安全假设”下，YASHE方案的IND-CPA安全性来自基于公钥加密方案的IND-CPA安全，而基于公钥加密方案的IND-CPA安全是基于RLWE困难问题。

要证明循环安全假设，需要方案设置的参数满足：

变为FHE#

如何将Leveled-FHE变为FHE，目前唯一的方法还是Gentry提出的“自举”（bootstrapping）技术。
即方案能够同态的计算自己的解密电路，这里需要用公钥将私钥的每一个比特加密，类似于密钥交换中的计算密，这里需要一个“安全假设”，即加密私钥的每个比特不会影响方案的安全性！

这里将解密电路的复杂度降低为O(log(log(q))+log(d))，具体是将缩放（scaling）和舍入（rounding）操作换成消耗更小的乘法和移位运算。最后的模2并不会增加计算深度。

YASHE的变体YASHE‘#

不同之处是同态乘法，YASHE‘中乘法的中间密文只是一个简单的多项式，而YASHE中的中间密文是一个多项式向量，这就导致了计算密钥evk中只需包含lw,q个多项式，而不是l3w,q个多项式，所以密钥交换更加简单了。下面介绍简化过程和噪音分析。

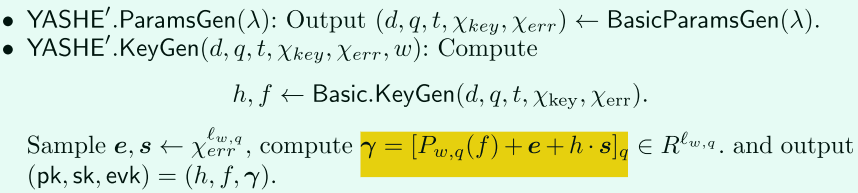
在YASHE方案中，˜cmult相当于是[m1.m2]t在D(f)⨂D(f)下加密的；而在YASHE‘方案中，˜cmult相当于是[m1.m2]t在f2下加密的。
可以看出，在新方案中，乘法中没有使用Decompt和PowerOfTwo技术，仅在密钥交换中使用到。

同态乘法#

这部分给出在乘法计算中，中间密文的噪音上限。

密钥交换#

同样，这里的evk可以看作是私钥f在公钥h下的加密。另外需要额外的“循环安全假设”保证方案的安全性。

正确性#

每一层的密文中的噪音大小是近似的，为了减少计算量，尽量使用更多的加法，使用更少的乘法。

这里给出密文的内在噪音的上限V、乘法深度L，与方案其它参数的关系，需要满足该条件才能执行L次乘法运算，即 Leveled-FHE方案。

安全性#

新方案的安全性依赖于RLWE问题、“循环安全假设”和DSPR问题，原方案可以根据根据参数设置而避免使用DSPR假设。
可以证明在RLWE问题和DSPR问题下，该方案是安全的，即方案的IND-CPA安全是基于RLWE假设和DSPR假设的。且需要满足于当 evk公开时，方案也是安全的。
这里给出一个更弱的DSPR假设（参数选取的分布不同，导致噪音上线不同）。
另外私钥一般取值很小，可以为每一个级提供一个公私钥对从而避免使用“循环安全假设”，此时每一层的evk和该层的公私钥有关，具体如下：

参数推荐#

这里给出了需要事先确定的两个重要参数：
（1）密文模数q
一般在64bit~1024bit之间取值
（2）多项式的级数
n=φ(d)一般取2的次幂，这里给出211和216。
（3）下面给出推荐参数，两种情况：固定q，求nmin，然后给出最大的层数Lmax；固定级数n，求最大的qmax，然后给出最大的层数Lmax

可以看出，随着参数的增大，支持计算的层数就变大，但计算量也随之变大。

（4）【Can homomorphic encryption be practical? 】中给出的实验结果
参数：R=Z[X]/(X4096+1),t=210,q:130bit
结果：加密：756ms，加法：4ms，乘法：1590ms，解密：57ms

（5）该方案的实验结果

代码不依赖于第三方库，基于C编写

参数：q:127bit,w=223，其它参数一样
结果：加密：27ms（百万次循环），加法：0.024ms（7万次循环），乘法：31ms（9070万循环），解密：5ms（1410万循环）

（6）方案的实际乘法次数为22～25，性能更好。

截断密文（Truncating）#

在Bra12中提出scale-变体的LWE方案，即丢弃密文最低位（least significant bits ），基于该思想，方案给出两种优化方向：

（1）约减密文长度
YASHE.Discardw(c,i)：输入一个密文和要被阶段的个数i，输出c′=⌊w−ic⌋，这里的w时基，一般取2。且wi.c′等于c的最低i位取0。
这里举例子：给出密文c=7=(0111)w，w=2
当i=2，c′=1，正好对应c去掉后两位得到的(01)w；且wi.c′=4，即(0100)w
当i=3，c′=0，正好对应c去掉后两位得到的(0)w；且wi.c′=0，即(0000)w

如果cf=Δm+v(modq)，则wic′f=Δm+v′(modq)

通过截取密文，密文的长度变短，且不依赖于q，而是依赖于q和噪音的比值。当用Dw,q(c)表示密文c时，大概需要logw(q/B)的基，且最低logw(B)位为0。

如果c在f2解密，则在密钥交换时，我们仅需要evk中的前logw(q/B)位的信息进行切换。

（2）约减计算密钥中元素个数
每次乘法，都需要减少evk中的元素数量。

通过CRT编码#

上面给出了推荐的参数和输入边界，以此来保证方案的正确性和安全性。
当需要更多的计算时，在不增加参数的情况下，使用该技术可以增大计算量。思想就是，利用中国剩余定理将多个输入编码为一个更大数，使得计算精度更好或者输入的数值更大。其中使用的参数一直不变，只需要密文个数变大。

通过CRT将每个输入编码为都是模ti的集合元素，来进行边界为B的整数计算；然后对集合进行计算，相当于对这些整数不涉及模约减（modular reductions）的运算，只要ti的乘积不超过B。集合中的每个整数都相当于对应模ti的明文（plain text）被加密的密文，并且能并行计算这些密文并返回结果；在解密时，利用CRT将输出或恢复为实际的整数。

此时的技术不同于【Batch fully homomorphic encryption over the integers】【Fully homomorphic simd operations】中的技术，这里没有利用CRT将信息打包到一个密文（single ciphertext）中的不同明文槽中（plain text slots）而是简单加密了一个密文中每一个CRT编码的部分，对应于模ti的明文（plain text ）。密文现在由多个环元素组成，但是可以并行计算，这可以使我们使用相同的参数处理双位（integers of double bit length）长的整数，仅使用不同的值t0,t1扩展到两个密文。

没看太懂。说的太抽象。没有具体例子。