-
吴恩达机器学习笔记(一)
机器学习(一)
学习机器学习过程中的心得体会以及知识点的整理,方便我自己查找,也希望可以和大家一起交流。
—— 吴恩达机器学习第一、二章 ——
一、概述
-
什么是机器学习
Arthur Samuel认为机器学习是在没有明确设置的情况下,是计算机具有学习能力的研究领域。Tom Mitchell认为A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its’performance at tasks in T, as measured by P, imporves with experience. 翻译过来就是:如果用P来衡量计算机程序在任务T上的性能,根据经验E在任务T上获得性能改善,那么我们称该程序从经验E中学习。
机器学习主要分为有监督学习和无监督学习以及还有强化学习和推荐系统等,通俗来说有监督学习就是我们教计算机做事情,无监督学习就是让计算机自己做事情。学术上讲,可以根据是否有label来区分监督学习和无监督学习。监督学习主要包括分类和回归两种形式,无监督学习主要包括聚类和关联分析。
-
有监督学习
有监督学习就是给算法一个数据集,其中包含了正确答案,算法的目的是给出更多的正确答案。
例如回归问题(预测连续数值输出)或者分类问题(预测离散值输出)等,算法的最终目的是解决无穷多个特征的数据集。 -
无监督学习
无监督学习就是只给算法一个数据集,但是不给数据集的正确答案,由算法自行分类。
聚类算法,主要应用例如:
● 每天收集几十万条新闻并按主题分好类
● 对用户进行分类来确定目标用户
● 鸡尾酒算法:两个麦克风分别离两个人不同距离,录制两段录音,将两个人的声音分离开来
二、单变量线性回归
-
概念
假设函数:
hθ(x) = θ0 + θ1x
代价函数:
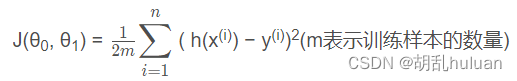
目标:
最小化代价函数,即minimize J(θ0, θ1)代价函数也被称为平方误差函数或者平方误差代价函数,在线性回归问题中,平方误差函数是最常用的手段。改变θ1的值,得到多组J(θ0),并作出下图(右):
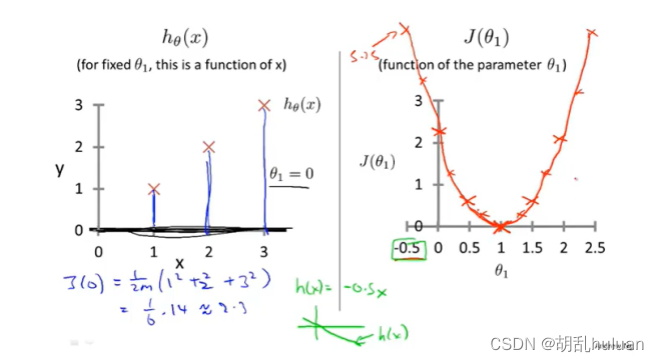
得到的minimize J(θ0) 就是线性回归的目标函数。
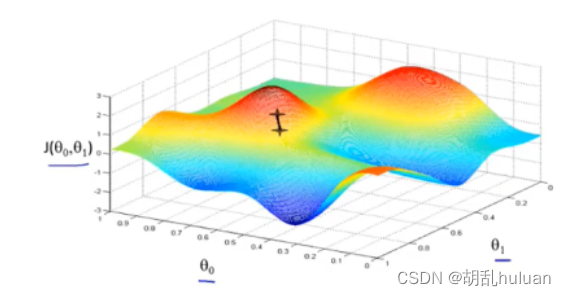
如果同时考虑θ0,和θ1如下图,曲面的高度就是J(θ0, θ1)的值。
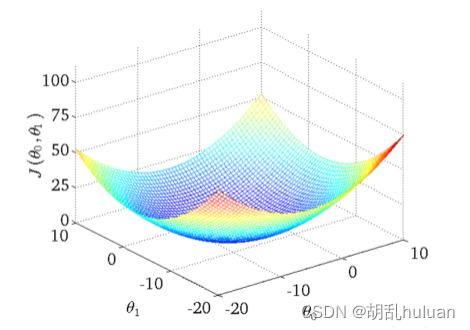
将三维图平面化后如下图所示,等高线的中心对应最小代价函数。
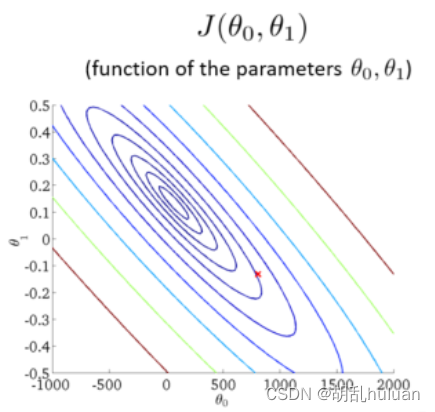
-
梯度下降
梯度指函数中某一点(x, y)的梯度代表函数在该点变化最快的方向,因此选用不同的点开始可能达到另一个局部最小值。
算法思路
● 指定θ0 和 θ1的初始值。
● 不断改变θ0和θ1的值,使J(θ0,θ1)不断减小。
● 得到一个最小值或局部最小值时停止。
梯度下降公式
● ,其中 α 为学习速率
● θ0和θ1应同步更新,否则如果先更新θ0,会使得θ1是根据更新后的θ0去更新的,与正确结果不相符。

对于其中的参数α,如果α选择太小,会导致每次移动的步幅都很小,最终需要很多步才能最终收敛;如果α选择太大,会导致每次移动的步幅过大,可能会越过最小值,无法收敛甚至会发发散。
实现原理
● 偏导表示的是斜率,斜率在最低点左边为负,最低点右边为正。 θj减去一个负数则向右移动,减去一个正数则向左移动。
● 在移动过程中,偏导值会不断变小,进而移动的步幅也不断变小,最后不断收敛直到到达最低点。
● 在最低点处偏导值为0,不再移动。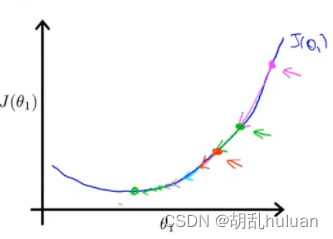
-
-
相关阅读:
Windows10下Maven3.9.5安装教程
uniAPP小程序 子组件使用watch不生效,H5正常,小程序不正常(其实是子组件model选项的问题)
Java update scheduler
Springboot文件上传
很多事情不是有意义了才做,而是因为做了才有意义
进阶JAVA篇-深入了解 Set 系列集合
SpringCloudAlibaba Seata在Openfeign跨节点环境出现全局事务Xid失效原因底层探究
CCF-CSP 29次 第五题【202303-5 施肥】
Linux-网卡和网络配置
el-popover放在el-table中点击无反应问题
- 原文地址:https://blog.csdn.net/qq_44867435/article/details/125005978