KMP算法(多种实现方式)

KMP算法核心思想

利用已经匹配的数据,去除无效的从头匹配

KMP算法流程

首先我们找到 i=9,j=9时不匹配,如果时暴力算法,此时i应重新来到i=2的位置,j返回j=1的位置,开始新一轮的匹配

这样暴力匹配,就白白浪费了已经匹配的串,那么问题来了,我们应该如何利用已经匹配的串呢??

我们看着图片,假设i返回i=2,j返回j=1,i++,j++,i指向b,j指向a,此时就不匹配了,又要重新开始,i来到3,j又回到j=1,双方指向第一个元素就不匹配,kmp算法的核心就是过滤掉这种低效的匹配,我们往下看

我们直到i=9和j=9前面的串 a a b a a b a a无论在S串或者J串是完全相等的,这也就意味着,我下面的操作无论在S串操作或者在J串操作,只要不出这个范围,在哪里操作都是一样的,因为他们都是同一串!

我们找到紧挨着i=9,元素b前的一串后缀(aabaa),一定要紧挨着,然后找到 J串从第一个元素开始的,与aabaa相等的前缀! 为什么要这样找呢?? 我们可以发现i从这个前缀的第一个元素开始能够完全匹配,J从第一个元素开始一直到这个缀结束,这样就可以过滤掉,大量的无效匹配,比如刚才的 i=2,i=3,都属于无效匹配

此时有个疑问,既然是紧挨着i=9的后缀,和J第一个元素出发的前缀,那么aa不可以吗?? 当然可以啦,从aa开始匹配,也就是i=7开始,新一轮匹配,但是这样会丢解,也就是,i跳的步子大了,跨过了可行解的下标!

通过上面的铺垫,我们引出一个概念

最长相等前后缀

从第一个元素开始,不包括最后一个元素结束,和从最后一个元素开始,不包括第一元素得出的前缀和后缀,前缀和后缀满足,相等且最长

通过上面讲解,我们就是要利用这个最长相等前后缀,达到过滤无效匹配的效果,上面讲过,我的操作完全可以只在J串进行,无需在S串进行,所以我让i=9不动,让J移动到J=5的位置,开始匹配i,和j+1所对应元素是否相等即可! 这也就相当于暴力算法,从i=4开始匹配,匹配到了i=8的位置,故通过寻找最长相等前后缀可以快速达到此效果!!

故:在使用kmp算法时,需要求出J串的每个位置的最长相等前后缀 (有的算法实现时会求出,每个位置 ‘前’ 的最长相等前后缀,这在后面会讲解,不同的求法,实现代码不同,因此会有差异)

求解Next数组

我们依J串为例a a b a a b a a a a求出它的Next数组(next数组存放每个位置的最长前后缀)

那么如何用代码实现呢?

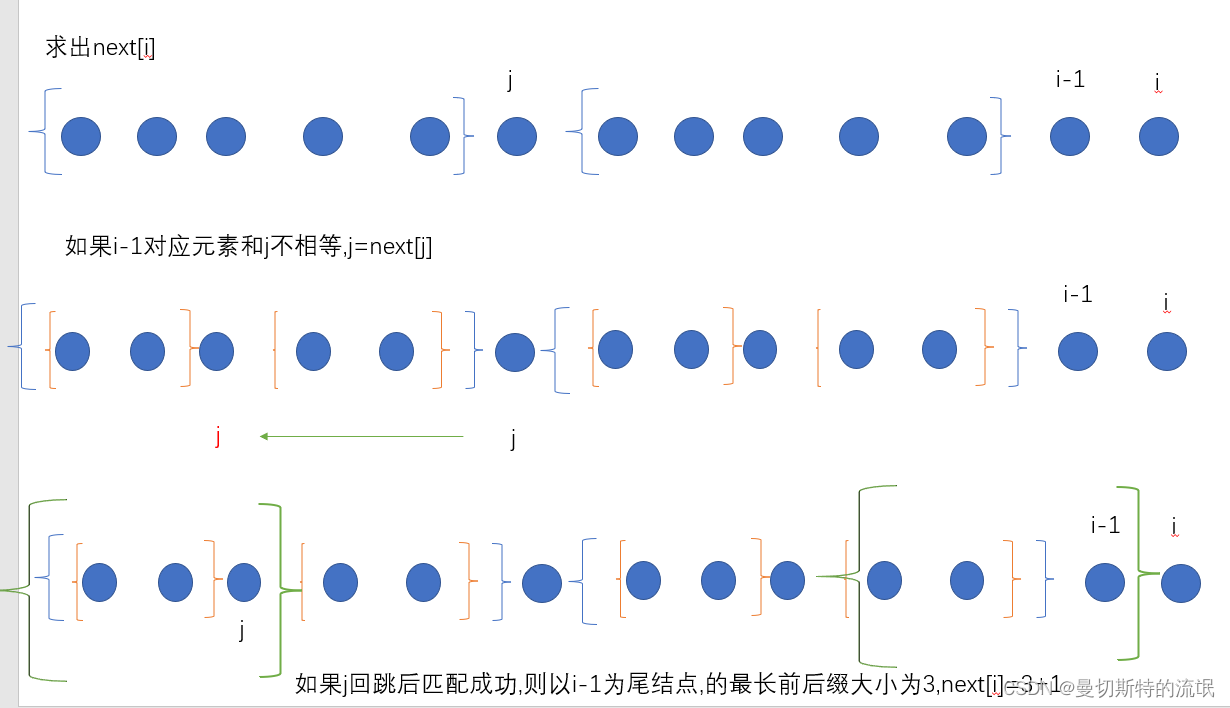
我们先观察next数组,我们发现只要多进来一个元素,并且满足最长前后缀,那么next数组就会增加1,那么如果不满足呢? 实际上我们观察代码可看到i起始从2开始,j从0开始,每次用j+1的位置进行匹配,我们可以理解为虽然用的是同一条串,但是由于i和j从不同起点出发导致,出现了一个新两个串匹配问题,那么就可以转化为我们刚刚讲的kmp思想

我们看以下匹配模拟过程

当i=9时,j=5,j+1元素为b与a并不匹配,也就意味着i=9无法继续发扬光大,无法继承上依次最大前后缀,所以需要寻找新的,也就回到了最初的两个串匹配问题,不同则回退,所以j回退到next[5]的位置(此时next[5]已经求出来了),j落到j=2,用j+1继续匹配i,发现匹配仍然失败b!=a,故j移动到next[j]位置也就是j=1,继续用j+1匹配,匹配成功,退出while循环,i++,j++,接着算出next[10]

这里解释以下为什么j从0开始,i从2开始,如果j从0开始,i从2开始,那么每次只需要用j+1去匹配i(“进可攻”),如果不匹配直接j=next[j] (“退可守”),所以我们现在的next数组含义是如果正在匹配的元素不相等,则需要他们之前的next[j],而不是他们自身的next[j],后面会讲解,直接利用自身的next不必需要前一个位置的next回退(一定注意区分)

模式串与主串匹配过程

这里的代码和求next函数代码十分相似,只是求next函数用的一个串,这里变为了两个串,注意起始位置,i从1开始j从0开始,之前是i从2开始,因为只有从2开始才能领先一个位置,用j+1去比较,不然j+1和i指向同一个元素无法达到进可攻退可守的效果!

竞赛版本代码

kmp模板题目洛谷P3375

#include <bits/stdc++.h>
using namespace std;
const int maxn=1e6+10;

int ne[maxn];
int la,lb; //主串长la,子串长lb
char a[maxn],b[maxn]; //a主串 b子串

int main()
{

    cin>>a+1;
    cin>>b+1;
    la=strlen(a+1);
    lb=strlen(b+1);
    //预处理next函数
    for(int i=2,j=0;i<=lb;i++)
    {
        while(j&&b[i]!=b[j+1])j=ne[j]; //如果不匹配每次向前跳
        if(b[i]==b[j+1])j++;//匹配则j指针前移
        ne[i]=j;
    }

    //根据next数组进行匹配
    for(int i=1,j=0;i<=la;i++)
    {
        while(j&&a[i]!=b[j+1])j=ne[j];//模式串前移动,也就是回跳
        if(a[i]==b[j+1])j++;
        if(j==lb)printf("%d\n",i-lb+1);
    }

    for(int i=1;i<=lb;i++)
    {
        cout<<ne[i]<<" ";
    }


    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

上面版本代码复杂,由于求next数组,遍历第一个for循环,里面还有while循环,并且i和j的起始位置,也不大相同,但是next数组的想法特别简单,就是求解到当前位置的,最长前后缀,我么针对next数组进行动手脚,进而简化代码,下面的代码也是考研常见的版本,竞赛中几乎不会使用这个版本,两个版本各有千秋!

对next数组修改

上面版本每次匹配都需要用j+1的位置去匹配,而非j自身,如果j+1不匹配j进行回退,那么反过来一想,能不能让j自身去匹配,如果不相等,则仍然是执行j=next[j]呢? (回退后仍然是j直接匹配)

答案是可以的!

我么将next数组元素值进行向右移动一位,然后+=1就可以达到此效果!

我们来手动解释以下,当向右移动一位后,next[j]的值表示,前一位的最长相等前后缀,我们此时移动到该位置发现需要用j+1去和i匹配,所以j还需要+=1,才能直接达到移动后直接和i去匹配的效果! (时刻记得和之前next数组的区别)

前面的next数组手推,是以当前元素为最后一个结点的最长前后缀,现在的next数组,需要考虑以前一个元素为结尾的最长前后缀长度然后在+=1即可,我们来手推以下!

手动匹配next数组方法

在当前元素,前画一个括弧,寻找括弧中最长前后缀,最后+=1

考研求解next数组代码

void get_next(String T,int next[])
{
    int i=1,j=0; //i领先一个位置
    next[1]=0;
    while(i<T.length)
    {
        if(j==0||T.ch[i]==T.ch[j]) //如果j=0时,意味着当前i无法和模式串匹配,i需要向后移动
        {
            i++;j++;             //i++相当于next[j]赋值给next[j+1],j++相当于移动到可以直接匹配的位置
            next[i]=j;
        }else{
            j=next[j]; //回退
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

这两个版本的代码差异挺大,主要是由于,next数组右移动一位,然后+=1造成的。初始时i=1,j=0,这样构成字符差,将一串字符划分为两串,然后while循环结束条件为i<T.length,由于最后一个位置的next[j]由next[j-1]向右移动,所以不需要遍历到i=T.length

if中的条件中j==0时,由于i和j一直不匹配导致,j=next[j]一直进行,所以最后移动到j=0,即i元素对应的子串,没有最长前后缀,所以需要next[i+1]应该跳到1号位置,注意:每次都是求前一个元素的最长前后缀,在赋值给当前元素,在代码中体现就是,满足if语句,然后i++,这个i++就是手动求next数组,向右移动一位,然后j++,对应如果发生回跳,应该跳到能够直接去匹配的位置,而不是最长前后缀的最后一位。

if语句中T.ch[i]==T.ch[j],注意此时i宏观上是i-1,也就是以前一个结点为最后结点的最长前后缀,需要注意next[i-1] 并不代表以i-1为最后一个结点的最长前后缀,所以第i-1对应元素作为需要和j匹配的元素,代码视觉上是i去匹配,实际上是i-1去匹配,如果匹配成功证明 i-1可以发扬光大,不过匹配失败,那么最长前后缀只好缩短!

来看下面图解

如果匹配不成功

考研版本代码

#include <bits/stdc++.h>
using namespace std;

#define MAXLEN 225

typedef struct
{
    char ch[MAXLEN];
    int length;
} String;

void get_next(String T,int next[])
{
    int i=1,j=0; //i领先一个位置
    next[1]=0;
    while(i<T.length)
    {
        if(j==0||T.ch[i]==T.ch[j]) //如果j=0时,意味着当前i无法和模式串匹配,i需要向后移动
        {
            i++;
            j++;             //i++相当于next[j]赋值给next[j+1],j++相当于移动到可以直接匹配的位置
            next[i]=j;
        }
        else
        {
            j=next[j]; //回退
        }
    }
}

int  Index_KMP(String S,String T,int next[])
{
    int i=1,j=1;
    while(i<=S.length&&j<=T.length)
    {
        if(j==0||S.ch[i]==T.ch[j])
        {
            i++,j++;//匹配成功,i和j向后移动
        }
        else
        {
            j=next[j];//j回调可以直接匹配的位置

        }
    }
    if(j>T.length) return i-T.length; //不需要+1,因为while1循环退出之前i++,用来while循环判断了
    else return 0;
}



int main()
{
    String s1,s2; //s1母串,s2子串
    char a[MAXLEN],b[MAXLEN];
    cout<<"输入母串:"<<endl; //aabaabaabaabaabaaaa
    cin>>s1.ch+1;
    s1.length=strlen(s1.ch)-1;
    cout<<"输入子串:"<<endl;//aabaabaaaa
    cin>>s2.ch+1;
    s2.length=strlen(s2.ch)-1;
    int next[MAXLEN];
    get_next(s2,next);
    cout<<"next数组如下"<<endl;
    for(int i=1;i<=s2.length;i++)
    {
        cout<<next[i]<<" ";
    }
    cout<<endl;
    printf("匹配位置:%d\n",Index_KMP(s1,s2,next));



    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76

运行结果

对KMP算法求解next数组优化(nextval)

由考研版本可知,next数组是回跳到可以直接匹配的位置,那么问题来了,当前i和j所对应元素发生不匹配,j进行回跳,如果回跳后的元素和回跳前的元素相当,那么岂不是白跳了,跳了也是不匹配!

我们看到i=4,j=4发生不匹配,子串前4个元素相同,那么按照之前的回跳方法需要先跳到j=3,仍然不匹配,在跳j=2,j=1,j=0,最后i++,元素b匹配失败,这样需要回跳好多步,导致性能退化。

解决方法很简单,只需要在求next数组过程中,判断以下当前元素和回跳后的元素是否相等即可,如果不相等,则next[i]=j,如果相等,则next[i]=next[j]即可有点递归感觉,只需要一次就可以,因为是从前向后找,所以前面的next[j]一定保证了不会跳到相同元素对应位置! (有动态规划的感觉了)

实现优化next数组代码

#include <bits/stdc++.h>
using namespace std;

#define MAXLEN 225

typedef struct
{
    char ch[MAXLEN];
    int length;
} String;



int  Index_KMP(String S,String T,int next[])
{
    int i=1,j=1;
    while(i<=S.length&&j<=T.length)
    {
        if(j==0||S.ch[i]==T.ch[j])
        {
            i++,j++;//匹配成功,i和j向后移动
        }
        else
        {
            j=next[j];//j回调可以直接匹配的位置

        }
    }
    if(j>T.length) return i-T.length; //不需要+1,因为while1循环退出之前i++,用来while循环判断了
    else return 0;
}

void get_nextval(String T,int nextval[])
{
    int i=1,j=0;
    while(i<T.length)
    {
        if(j==0||T.ch[i]==T.ch[j])
        {
            i++,j++;
            if(T.ch[i]!=T.ch[j])
            {
                nextval[i]=j;  //如果不相等正常赋值
            }
            else
            {
                nextval[i]=nextval[j]; //相等时
            }
        }
        else
        {
            j=nextval[j];
        }
    }
}


int main()
{
    String s1,s2; //s1母串,s2子串
    char a[MAXLEN],b[MAXLEN];
    cout<<"输入母串:"<<endl; //aaabaaaab
    cin>>s1.ch+1;
    s1.length=strlen(s1.ch)-1;
    cout<<"输入子串:"<<endl;//aaaab
    cin>>s2.ch+1;
    s2.length=strlen(s2.ch)-1;
    int next[MAXLEN];
    get_nextval(s2,next);
    cout<<"nextval数组如下"<<endl;
    for(int i=1; i<=s2.length; i++)
    {
        cout<<next[i]<<" ";
    }
    cout<<endl;
    printf("匹配位置:%d\n",Index_KMP(s1,s2,next));



    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82

KMP算法复杂度分析

母串长n,模式串(子串)长m

首先我们分析一下暴力版本复杂度,i需要从1回退,2回退,3回退,一共回退n次,j每一次回退后都需要遍历自身长度,那么就需要n乘以m次操作,O(nm)

kmp算法i并不会回退,所以i从1到n一共执行n次操作故复杂度O(n),不要忘记还要求next数组的复杂度,求next数组,和kmp一样都i都不会回溯,所以为O(m),故总时间复杂度O(n+m),这个复杂度在代码上很好理解,尤其是考研版本的代码,只需要一个while循环!

总结

整体来说kmp算法,初学复杂,尤其是对于next数组,不同求解,不同含义,容易让人混淆,笔者在这里对next数组来龙去脉进行贯穿讲解,分成了竞赛版,和考研版本,大家各取所需!竞赛版本,next数组想法十分简单,实现起来比考研版本复杂,但考研版本next数组含义复杂,代码实现简单,不过对i位置的理解容易懵掉,大家加油!!!

感谢大家观看,感谢B站董晓算法,十分感谢!
董晓算法讲解kmp