0. 引言

在深度学习（图像领域）中，为了提升训练样本数量数据增强是非常常见的手段。比如：

• 随机水平翻转
• 随机色调(H)、饱和度(S)、明度(V)调整
• 随机旋转，缩放，平移以及错切
• 还有近几年常用的mixup，mosaic等等。

本文涉及的内容有：—— 使用OpenCV进行演示

1. 随机旋转
2. 缩放
3. 平移
4. 错切(shear)

1. 仿射变换（Affine Transformation）

仿射变换，又称仿射映射，是指在几何中，一个向量空间进行一次线性变换并接上一个平移，变换为另一个向量空间。 仿射变换是在几何上定义为两个向量空间之间的一个仿射变换或者仿射映射（来自拉丁语，affine，“和…相关”）由一个非奇异的线性变换(运用一次函数进行的变换)接上一个平移变换组成。

简单来说，“仿射变换”就是：“线性变换”+“平移”。

1.1 线性变换

1.1.1 定义

线性映射（ linear mapping）是从一个向量空间 $\mathbb{V}$ 到另一个向量空间 $\mathbb{W}$ 的映射且保持加法运算和数量乘法运算，而线性变换（linear transformation）是线性空间 $\mathbb{V}$ 到其自身的线性映射（linear transformation）。

实际上线性变换可以理解为在有一定条件（后面会细讲）的一个函数，实现将一个向量映射到另一个向量的效果。

1.1.2 常见的线性变换操作

举一些例子就很清楚在深度学习数据增强中线性变换是什么了，常见的的线性变换有：

1. 旋转
2. 图像拉伸
3. 缩放
4. 投影
5. 镜像
6. 错切(shear)
7. …

值得注意的是，平移并不是线性变换。

1.1.3 线性变换的特点

线性变换有三个特点：

1. 变换前是直线，变换后依然是直线；
2. 直线比例保持不变
3. 变换前是原点，变换后依然是原点

1.1.4 旋转的实现原理

图来源：https://blog.csdn.net/weixin_41107577/article/details/115356839

举这个例子的目的是想明白一件事情，就是矩阵的线性变换都是可以通过乘一个变换矩阵完成的。换到数据增强上，图片的旋转、缩放等一系列线性变换的操作其实也可以通过求一个变换矩阵，之后让我们的图片与变换矩阵相乘得到我们的目的矩阵。

1.2 平移

“仿射变换”就是：“线性变换”+“平移”。刚才我们讲了线性变换，接下来看一下平移是怎么操作的。图来源仍是https://blog.csdn.net/weixin_41107577/article/details/115356839。

平移属于仿射变换

1.3 仿射变换的特点

1. 变换前是直线，变换后依然是直线；
2. 直线比例保持不变

相比线性变换而言，少了原点保持不变这一条。主要的原因就是因为仿射变换包含平移。

2. OpenCV中的仿射变换

一般数据增强使用的库有：①Pillow；②OpenCV。一般而言使用OpenCV居多（因其功能齐全）。在OpenCV中可以通过仿射变换来实现①旋转，②缩放，③平移以④及错切等一系列操作。仿射变换的矩阵乘法形式如下：

[ x ′ y ′ 1 ] = [ m 11 m 12 m 13 m 21 m 22 m 23 0 0 1 ] [ x y 1 ] \left[

\right] = \left[ \right] \left[ \right] ⎣⎡​x′y′1​⎦⎤​=⎣⎡​m11​m21​0​m12​m22​0​m13​m23​1​⎦⎤​⎣⎡​xy1​⎦⎤​

其中x , $x,y$是变换前的坐标，$x^{\prime },y^{\prime }$是变换后的坐标。其中$m_{11},m_{12},m_{21},m_{22}$为线性变换参数，$m_{13},m_{23}$为平移参数。如果仿射矩阵是对角矩阵，相当于不做任何操作。

我们看上面的公式其实可以发现，和1.1.4、1.2中的示例是一个意思。

注意：变换矩阵在图片矩阵的左侧。

OpenCV中仿射变换的流程如下：

2.1 旋转、平移、缩放操作

首先再次强调下图像处理中的坐标系，水平向右为$x$轴正方向，竖直向下为$y$轴正方向。

对于图像的旋转，缩放，平移都可以直接通过使用OpenCV提供的getRotationMatrix2D方法来求得仿射矩阵，

getRotationMatrix2D官方文档

需要传入

• 旋转中心center
• 旋转角度angle（逆时针为正）
• 以及缩放因子scale

变换将旋转中心映射到自身。
参数

• center 源图像中的旋转中心。
• angle 以度为单位的旋转角度。 正值表示逆时针旋转（假设坐标原点为左上角）。
• scale 各向同性比例因子。

假设以图片中心为旋转中心，顺时针旋转30度（OpenCV里是以逆时针为正，所以angle=-30），并缩放0.5倍：

import cv2


img = cv2.imread("img_exp.jpg")  # 默认以彩色BGR格式读入图片
h, w = img.shape[0], img.shape[1]  # 获取图片的高度和宽度

"""
    + center: 旋转中心
    + angle: 旋转角度（逆时针为正）
    + scale: 缩放因子
"""
M = cv2.getRotationMatrix2D(center=(w//2, h//2), 
                            angle=-30, 
                            scale=0.5)
print(f"仿射矩阵: \n{M}")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

得到如下的仿射矩阵（旋转矩阵）：

仿射矩阵: 
[[  0.4330127   -0.25       145.55771366]
 [  0.25         0.4330127   53.65578987]]
1
2
3

接着使用OpenCV中的warpAffine的方法利用求得的仿射矩阵M做仿射变换，

warpAffine官方文档

其中

• src为原图像
• dsize为输出图像的大小
• borderValue为边界填充颜色（注意OpenCV默认读取通道为BGR顺序，(0,0,0)代表黑色）

import cv2


img = cv2.imread("img_exp.jpg")  # 默认以彩色BGR格式读入图片
h, w = img.shape[0], img.shape[1]  # 获取图片的高度和宽度

# 根据传入的参数计算仿射矩阵M
M = cv2.getRotationMatrix2D(center=(w//2, h//2),  # 旋转中心
                            angle=-30,  # 旋转角度
                            scale=0.5)  # 缩放因子
print(f"仿射矩阵: \n{M}")

# 根据仿射矩阵M对图片执行仿射变换
affined_img = cv2.warpAffine(src = img,  # 被执行图片
                             M = M,  # 仿射矩阵
                             dsize = (w, h),  # 输出图片大小
                             borderValue = (0, 0, 0))  # 边界填充值

# 显示原图和经过仿射变换后的图
cv2.imshow("origin", img)
cv2.imshow("affined img", affined_img)
cv2.waitKey()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

结果如下：

如图，左边是原图，右边是旋转、缩放、平移后的图片。

注意，旋转后如果有超出指定范围dsize的像素都会被截去。我们可以尝试一下将desize=(w//2, h//2)：

2.2 上一节操作的理论讲解

https://blog.csdn.net/qq_37541097/article/details/119420860

接着结合上面的仿射变换公式来讲。其中$m_{11},m_{12},m_{21},m_{22}$为线性变换参数（沿坐标原点旋转就是一个简单的线性变换），$m_{13},m_{23}$为平移参数（分别对应x轴方向平移和y轴方向平移）。

[ m 11 m 12 m 13 m 21 m 22 m 23 0 0 1 ] \left[

\right] ⎣⎡​m11​m21​0​m12​m22​0​m13​m23​1​⎦⎤​

上一节的操作可以分解为如下三步

1. 沿坐标原点旋转
2. 缩放图片
3. 平移图片

前两步属于线性变换，最后一步属于仿射变换

2.2.1 旋转

对于第一步的原点旋转对应的仿射矩阵为：

# 根据传入的参数计算仿射矩阵M
M = cv2.getRotationMatrix2D(center=(0, 0),  # 旋转中心
                            angle=-30,  # 旋转角度
                            scale=1.0)  # 缩放因子
print(f"仿射矩阵: \n{M}")

"""
仿射矩阵: 
[[ 0.8660254 -0.5        0.       ]
 [ 0.5        0.8660254  0.       ]]
"""
1
2
3
4
5
6
7
8
9
10
11

[ 0.866 − 0.5 0 0.5 0.866 0 0 0 1 ] \left[

\right] ⎣⎡​0.8660.50​−0.50.8660​001​⎦⎤​

当然这里也可以直接使用旋转矩阵模板来计算，但需要注意的是模板里的旋转矩阵默认y轴是竖直向上的，但图像处理中y轴是竖直向下的，且都是以逆时针旋转为正，所以这里的 $\theta =30°$：

[ cos ⁡ ( θ ) − sin ⁡ ( θ ) 0 sin ⁡ ( θ ) cos ⁡ ( θ ) 0 0 0 1 ] \left[

\right] ⎣⎡​cos(θ)sin(θ)0​−sin(θ)cos(θ)0​001​⎦⎤​

2.2.2 缩放

对于第二步图片的缩放，直接使用如下缩放矩阵：

[ S x 0 0 0 S y 0 0 0 1 ] \left[

\right] ⎣⎡​Sx​00​0Sy​0​001​⎦⎤​

假设要将图片缩放0.5倍，那么缩放矩阵为：
[ 0.5 0 0 0 0.5 0 0 0 1 ] \left[

\right] ⎣⎡​0.500​00.50​001​⎦⎤​

2.2.3 将线性变换的变换矩阵进行组合

因为旋转和缩放都属于线性变换（平移是仿射变换），所以二者是可以组合的，由于两个线性变换矩阵满足结合律（在本章开头我们就说了，变换矩阵在图片矩阵的左侧），所以：

[ x ′ y ′ 1 ] 线 性 变 换 后 的 矩 阵 = [ 0.5 0 0 0 0.5 0 0 0 1 ] 缩 放 矩 阵 [ 0.866 − 0.5 0 0.5 0.866 0 0 0 1 ] 旋 转 矩 阵 [ x y 1 ] 图 片 矩 阵 = [ 0.433 − 0.25 0 0.25 0.433 0 0 0 1 ] 旋 转 缩 放 矩 阵 [ x y 1 ] 图 片 矩 阵

线性变换后的矩阵⎣⎡​x′y′1​⎦⎤​​​=缩放矩阵⎣⎡​0.500​00.50​001​⎦⎤​​旋转矩阵⎣⎡​0.8660.50​−0.50.8660​001​⎦⎤​​图片矩阵⎣⎡​xy1​⎦⎤​​=旋转缩放矩阵⎣⎡​0.4330.250​−0.250.4330​001​⎦⎤​​图片矩阵⎣⎡​xy1​⎦⎤​​​

2.2.4 平移 —— 仿射变换

对于第三步图片的平移，即将旋转、缩放后的图像中心移至原图像中心。这里示例中的图片$w=360,h=349$，故原图片中心点坐标是$(180,174)$ ，旋转后的中心点坐标是$(34.44,120.342)$：

import numpy as np

M = np.array([[0.433, -0.25, 0], [0.25, 0.433, 0], [0, 0, 1]])
center_matrix = np.array([180, 174, 1])

print(f"平移后中心点坐标为： \n{M @ center_matrix}")

"""

平移后中心点坐标为： 
[ 34.44  120.342   1.   ]
"""
1
2
3
4
5
6
7
8
9
10
11
12

[ 34.44 120.342 1 ] 旋 转 后 的 中 心 点 = [ 0.433 − 0.25 0 0.25 0.433 0 0 0 1 ] 旋 转 缩 放 矩 阵 [ 180 174 1 ] 中 心 点 矩 阵 \underset{旋转后的中心点}{ \left[

\right]} = \underset{旋转缩放矩阵}{ \left[ \right]} \underset{中心点矩阵}{ \left[ \right]} 旋转后的中心点⎣⎡​34.44120.3421​⎦⎤​​=旋转缩放矩阵⎣⎡​0.4330.250​−0.250.4330​001​⎦⎤​​中心点矩阵⎣⎡​1801741​⎦⎤​​

所以需要向 x 轴正方向平移 $180-34.44=145.56$ ，向 y 轴正方向平移 $174-120.342=53.658$，刚上面说了$m_{13},m_{23}$为平移参数（分别对应x轴方向平移和y轴方向平移）所以$m_{13}=145.56,m_{23}=53.658$（在对角矩阵的基础上设置$m_{13},m_{23}$即可）

[ 1 0 145.56 0 1 53.658 0 0 1 ] 平 移 矩 阵 \underset{平移矩阵}{ \left[

\right]} 平移矩阵⎣⎡​100​010​145.5653.6581​⎦⎤​​

和旋转缩放后的仿射矩阵进一步结合起来：

import numpy as np

translation_matrix = np.array([[1, 0, 145.56], [0, 1, 53.658], [0, 0, 1]])
M = np.array([[0.433, -0.25, 0], [0.25, 0.433, 0], [0, 0, 1]])

print(f"[平移矩阵][旋转缩放矩阵]： \n{translation_matrix @ M}")

"""
[平移矩阵][旋转缩放矩阵]： 
[[  0.433  -0.25  145.56 ]
 [  0.25    0.433  53.658]
 [  0.      0.      1.   ]]
"""
1
2
3
4
5
6
7
8
9
10
11
12
13

[ x ′ y ′ 1 ] 线 性 变 换 后 的 矩 阵 = [ 1 0 145.56 0 1 53.658 0 0 1 ] 平 移 矩 阵 [ 0.433 − 0.25 0 0.25 0.433 0 0 0 1 ] 旋 转 缩 放 矩 阵 [ x y 1 ] 图 片 矩 阵 = [ 0.433 − 0.25 145.56 0.25 0.433 53.658 0 0 1 ] 完 整 的 仿 射 矩 阵 [ x y 1 ] 图 片 矩 阵

线性变换后的矩阵⎣⎡​x′y′1​⎦⎤​​​=平移矩阵⎣⎡​100​010​145.5653.6581​⎦⎤​​旋转缩放矩阵⎣⎡​0.4330.250​−0.250.4330​001​⎦⎤​​图片矩阵⎣⎡​xy1​⎦⎤​​=完整的仿射矩阵⎣⎡​0.4330.250​−0.250.4330​145.5653.6581​⎦⎤​​图片矩阵⎣⎡​xy1​⎦⎤​​​

这个矩阵刚好和前面使用OpenCV方法cv2.getRotationMatrix2D(center=(w // 2, h // 2), angle=-30, scale=0.5)得到的矩阵是一样的。

处理的顺序非常重要，先旋转，在缩放，最后平移（顺序不一样结果不同）

OpenCV中得到的矩阵是$2\times 3$的，我们自己刚刚算的是$3\times 3$的仿射矩阵，最后使用cv2.warpAffine时只用传入前两行就行了。使用$3\times 3$的矩阵是为了方便将多个仿射矩阵进行相乘操作。

2.3 错切 —— shear

图像的错切(shear)变换实际上是平面景物在投影平面上的非垂直投影效果。图像错切变换也称为图像剪切、错位或错移变换。一般错切分为

• 横向错切
• 纵向错切
• 两个方向同时错切

在OpenCV中并没有直接针对错切生成仿射矩阵的方法，所以我们需自己可以构建错切对应的仿射矩阵，然后利用cv2.warpAffine进行仿射变换即可。下面是错切对应的仿射矩阵，其中 $\theta$ 表示错切角度，$\tan ({\theta }_1)$ 是x轴方向的错切参数，$\tan ({\theta }_2)$ 是y轴方向的错切参数。

2.3.1 沿着x方向shear

[ x ′ y ′ 1 ] = [ 1 tan ⁡ ( θ 1 ) 0 tan ⁡ ( θ 2 ) 1 0 0 0 1 ] [ x y 1 ] \left[

\right] = \left[\right] ⎣⎡​x′y′1​⎦⎤​=⎣⎡​1tan(θ2​)0​tan(θ1​)10​001​⎦⎤​⎣⎡​xy1​⎦⎤​

假设要沿水平方向错切$30°$，那么仿射矩阵为：

[ 1 tan ⁡ ( 30 ° ) 0 tan ⁡ ( 30 ° ) 1 0 0 0 1 ] = [ 1 0.577 0 0 1 0 0 0 1 ]

= ⎣⎡​1tan(30°)0​tan(30°)10​001​⎦⎤​=⎣⎡​100​0.57710​001​⎦⎤​

import cv2
import numpy as np
import math


img = cv2.imread("img_exp.jpg")  # 默认以彩色BGR格式读入图片
h, w = img.shape[0], img.shape[1]  # 获取图片的高度和宽度

origin_coordinate = np.array([[0, 0, 1], [w, 0, 1], [w, h, 1], [0, h, 1]])

print(f"原始的图像坐标矩阵为: \n{origin_coordinate}")
"""
[[  0   0   1]
 [360   0   1]
 [360 349   1]
 [  0 349   1]]
"""

# 定义错切角度
theta = 30  # shear角度
tan = math.tan(math.radians(theta))  # 将角度转为弧度再计算tan

# x方向shear
M = np.eye(3)
M[0, 1] = tan

# 计算shear坐标矩阵
shear_coordinate = (M @ origin_coordinate.T).T.astype(int)
print(f"shear坐标矩阵为: \n{shear_coordinate}")
"""
shear坐标矩阵为: 
[[  0   0   1]
 [360   0   1]
 [561 349   1]
 [201 349   1]]
"""

# 应用仿射变换
shear_img = cv2.warpAffine(src = img, 
                           M = M[:2],  # 仿射变换一般前两行就够了
                           dsize=(np.max(shear_coordinate[:, 0]),  # height
                                  np.max(shear_coordinate[:, 1])),  # width
                           borderValue = (0, 0, 0))  # 边界填充值
cv2.imshow("origin", img)
cv2.imshow("shear", shear_img)
cv2.waitKey(0)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

2.3.2 沿着y方向shear

import cv2
import numpy as np
import math


img = cv2.imread("img_exp.jpg")  # 默认以彩色BGR格式读入图片
h, w = img.shape[0], img.shape[1]  # 获取图片的高度和宽度

origin_coordinate = np.array([[0, 0, 1], [w, 0, 1], [w, h, 1], [0, h, 1]])

print(f"原始的图像坐标矩阵为: \n{origin_coordinate}")
"""
[[  0   0   1]
 [360   0   1]
 [360 349   1]
 [  0 349   1]]
"""

# 定义错切角度
theta = 30  # shear角度
tan = math.tan(math.radians(theta))  # 将角度转为弧度再计算tan

# x方向shear
M = np.eye(3)
M[1, 0] = tan

# 计算shear坐标矩阵
shear_coordinate = (M @ origin_coordinate.T).T.astype(int)
print(f"shear坐标矩阵为: \n{shear_coordinate}")
"""
shear坐标矩阵为: 
[[  0   0   1]
 [360 207   1]
 [360 556   1]
 [  0 349   1]]
"""

# 应用仿射变换
shear_img = cv2.warpAffine(src = img, 
                           M = M[:2],  # 仿射变换一般前两行就够了
                           dsize=(np.max(shear_coordinate[:, 0]),  # height
                                  np.max(shear_coordinate[:, 1])),  # width
                           borderValue = (0, 0, 0))  # 边界填充值
cv2.imshow("origin", img)
cv2.imshow("shear_y", shear_img)
cv2.waitKey(0)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

2.3.3 沿着x和y方向同时shear

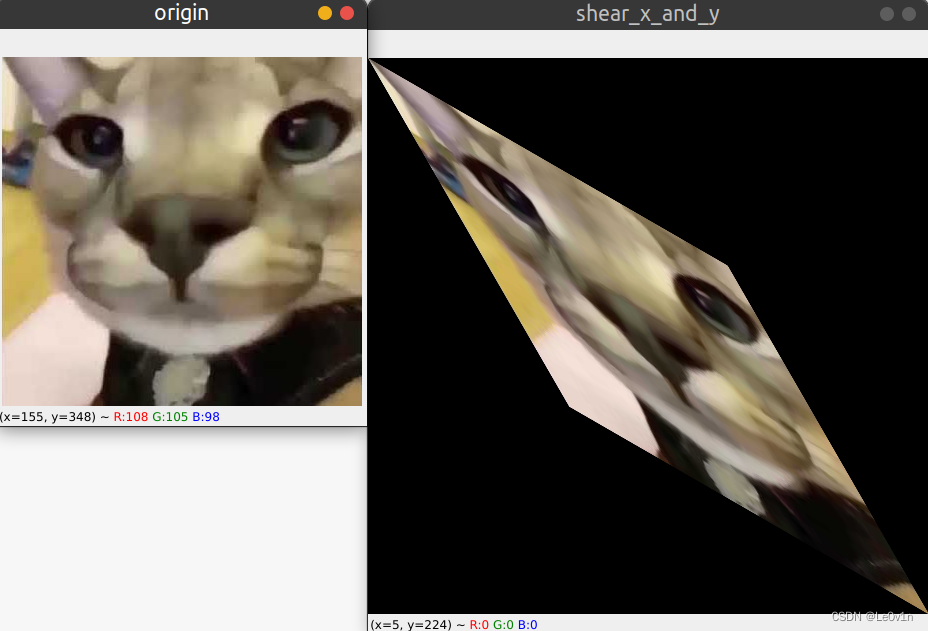
import cv2
import numpy as np
import math


img = cv2.imread("img_exp.jpg")  # 默认以彩色BGR格式读入图片
h, w = img.shape[0], img.shape[1]  # 获取图片的高度和宽度

origin_coordinate = np.array([[0, 0, 1], [w, 0, 1], [w, h, 1], [0, h, 1]])

print(f"原始的图像坐标矩阵为: \n{origin_coordinate}")
"""
[[  0   0   1]
 [360   0   1]
 [360 349   1]
 [  0 349   1]]
"""

# 定义错切角度
theta = 30  # shear角度
tan = math.tan(math.radians(theta))  # 将角度转为弧度再计算tan

# x方向shear
M = np.eye(3)
M[1, 0] = tan
M[0, 1] = tan

# 计算shear坐标矩阵
shear_coordinate = (M @ origin_coordinate.T).T.astype(int)
print(f"shear坐标矩阵为: \n{shear_coordinate}")
"""
shear坐标矩阵为: 
[[  0   0   1]
 [360 207   1]
 [561 556   1]
 [201 349   1]]
"""

# 应用仿射变换
shear_img = cv2.warpAffine(src = img, 
                           M = M[:2],  # 仿射变换一般前两行就够了
                           dsize=(np.max(shear_coordinate[:, 0]),  # height
                                  np.max(shear_coordinate[:, 1])),  # width
                           borderValue = (0, 0, 0))  # 边界填充值
cv2.imshow("origin", img)
cv2.imshow("shear_x_and_y", shear_img)
cv2.waitKey(0)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

3. YOLO v3-SPP关于仿射变换的代码

def random_affine(img, targets=(), degrees=10, translate=.1, scale=.1, shear=10, border=0):
    """
    使用OpenCV对图片进行一列仿射变换：
        随机旋转
        缩放
        平移
        错切
    Args:
        img: 四合一图片 -> img4
        labels：四合一图片的标签 -> labels4
        degrees: 超参数文件中定义的角度（旋转角度） -> 0.0
        translate: 超参数文件中定义的变换方式（平移） -> 0.0
        scale: 超参数文件中定义的scale（缩放） -> 0.0
        shear: 超参数文件中定义的修建（错切） -> 0.0
        border: 这里传入的是（填充大小） -s//2
    """
    # torchvision.transforms.RandomAffine(degrees=(-10, 10), translate=(.1, .1), scale=(.9, 1.1), shear=(-10, 10))
    # https://medium.com/uruvideo/dataset-augmentation-with-random-homographies-a8f4b44830d4
    # targets = [cls, xyxy]

    # 最终输出的图像尺寸，等于img4.shape / 2
    """
        img.shape[0], img.shape[1]为Mosaic相框的宽度和高度（是期待输出图像的两倍）
        因为传入的border=-s//2
            border * 2 -> -s
        所以height和width这个参数和我们期待Mosaic增强的输出是一样的（原图大小而非两倍）
    """
    height = img.shape[0] + border * 2
    width = img.shape[1] + border * 2

    # Rotation and Scale
    # 生成旋转以及缩放矩阵
    R = np.eye(3)  # 生成对角阵
    a = random.uniform(-degrees, degrees)  # 随机旋转角度
    s = random.uniform(1 - scale, 1 + scale)  # 随机缩放因子
    R[:2] = cv2.getRotationMatrix2D(angle=a, center=(img.shape[1] / 2, img.shape[0] / 2), scale=s)

    # Translation
    # 生成平移矩阵
    T = np.eye(3)
    T[0, 2] = random.uniform(-translate, translate) * img.shape[0] + border  # x translation (pixels)
    T[1, 2] = random.uniform(-translate, translate) * img.shape[1] + border  # y translation (pixels)

    # Shear
    # 生成错切矩阵
    S = np.eye(3)
    S[0, 1] = math.tan(random.uniform(-shear, shear) * math.pi / 180)  # x shear (deg)
    S[1, 0] = math.tan(random.uniform(-shear, shear) * math.pi / 180)  # y shear (deg)

    # Combined rotation matrix
    """
        @ 表示矩阵相乘（就是传统意义的矩阵相乘而非对应元素相乘）
    """
    M = S @ T @ R  # ORDER IS IMPORTANT HERE!!
    if (border != 0) or (M != np.eye(3)).any():  # image changed
        # 进行仿射变化
        img = cv2.warpAffine(img, M[:2], dsize=(width, height), flags=cv2.INTER_LINEAR, borderValue=(114, 114, 114))

    """
        对图片进行仿射变换后，对它的labels同样也要做对应的变换
    """
    # Transform label coordinates
    n = len(targets)
    if n:
        """
            将GTBox4个顶点坐标求出来再进行仿射变换
        """
        # warp points
        xy = np.ones((n * 4, 3))
        xy[:, :2] = targets[:, [1, 2, 3, 4, 1, 4, 3, 2]].reshape(n * 4, 2)  # x1y1, x2y2, x1y2, x2y1
        # [4*n, 3] -> [n, 8]
        xy = (xy @ M.T)[:, :2].reshape(n, 8)  # 得到经过放射变换后4个顶点的坐标

        """
            求出4个顶点进行仿射变换之后的xy坐标
            取4个顶点的(x_min, y_min)作为新的GTBox的左上角坐标
            取4个顶点的(x_max, y_max)作为新的GTBox的右下角坐标
            
            为什么这么做呢？
                比如我们的GTBox是一个正常的矩形框，在经过仿射变换后它变成了倾斜的矩形框，但在目标检测中，矩形框一般是正的，不是倾斜的
                所以需要对它的矩形框进行一个重新的调整 -> 这样就求出新的GTBox的合适的坐标了
        """
        # create new boxes
        # 对transform后的bbox进行修正(假设变换后的bbox变成了菱形，此时要修正成矩形)
        x = xy[:, [0, 2, 4, 6]]  # [n, 4]
        y = xy[:, [1, 3, 5, 7]]  # [n, 4]
        xy = np.concatenate((x.min(1), y.min(1), x.max(1), y.max(1))).reshape(4, n).T  # [n, 4]

        # reject warped points outside of image
        # 对坐标进行裁剪，防止越界
        xy[:, [0, 2]] = xy[:, [0, 2]].clip(0, width)
        xy[:, [1, 3]] = xy[:, [1, 3]].clip(0, height)
        w = xy[:, 2] - xy[:, 0]  # 计算新的GTBox的宽度
        h = xy[:, 3] - xy[:, 1]  # 计算新的GTBox的高度

        # 计算调整后的每个box的面积
        area = w * h

        # 计算调整前的每个box的面积（在对标签仿射变换之前GTBox的面积）
        area0 = (targets[:, 3] - targets[:, 1]) * (targets[:, 4] - targets[:, 2])

        # 计算仿射变换之后每个GTBox的比例
        ar = np.maximum(w / (h + 1e-16), h / (w + 1e-16))  # aspect ratio

        # 选取长宽大于4个像素，且调整前后面积比例大于0.2，且比例小于10的box -> mask
        i = (w > 4) & (h > 4) & (area / (area0 * s + 1e-16) > 0.2) & (ar < 10)

        # 筛选GTBox
        targets = targets[i]

        # 使用新的GTBox信息替换原来的
        targets[:, 1:5] = xy[i]

    return img, targets
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114

参考

1. https://blog.csdn.net/qq_37541097/article/details/119420860
2. https://blog.csdn.net/weixin_41107577/article/details/115356839
3. https://docs.opencv.org
4. https://blog.csdn.net/u012005313/article/details/46674305