24/8/15算法笔记 复习_决策树

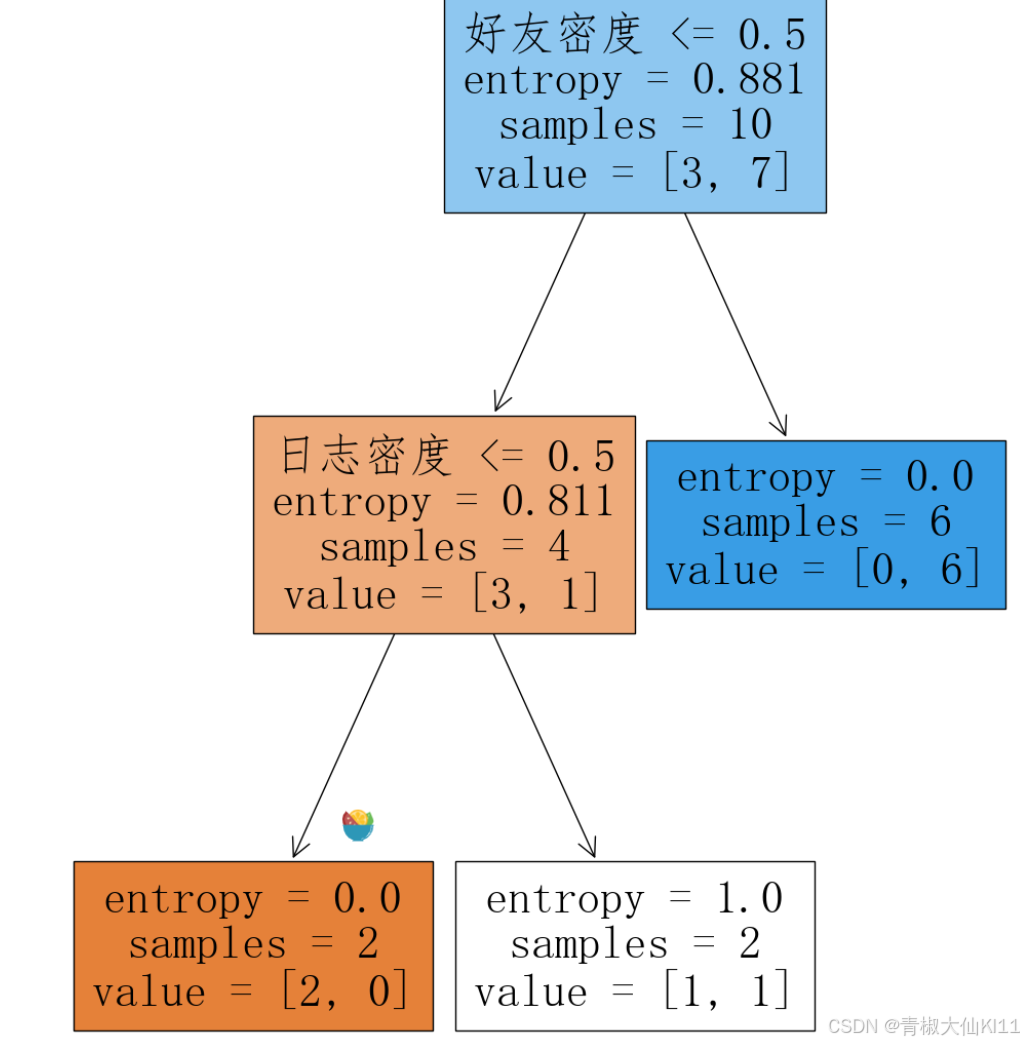
#手动计算决策树到底是如何实现分类的
p1 = (y =='N').mean()
p2 = (y =='Y').mean()
 
p1 * np.log2(1/p1) +p2*np.log2(1/p2)
X['真实用户'] = y
x = X['日志密度'].unique()#.unique() 是一个方法，它返回一个数组，包含 X['日志密度'] 列中所有不同的值。
x.sort()#排序
print(x)
 
#目的是通过遍历可能的分割点来计算信息熵，进而评估数据在不同分割点的概率分布。
for i in range(len(x)-1):
    split = x[i:i+2].mean()
    #概率分布
    cond = X['日志密度']<=split
    
    #左边概率是多少，右边是多少
    p = cond.value_counts()/cond.size  #计算满足条件和不满足条件的样本数量，并将其归一化以得到概率分布。
    indexs = p.index
    entropy = 0
    for index in indexs:
        user = X[cond ==index]['真实用户']#取出了目标值y的数据 # 这行代码的目的是过滤X DataFrame，只保留那些满足cond条件等于当前index的行，并从这些行中提取'真实用户'列。
        
        p_user = user.value_counts()/user.size
        #每个分支的信息熵
        entropy += (p_user*np.log2(1/p_user)).sum()*p[index]
    print(split,entropy)

x = X['好友密度'].unique()
x.sort()#排序
print(x)
for i in range(len(x)-1):
    split = x[i:i+2].mean()
    #概率分布
    cond = X['好友密度']<=split
    
    #左边概率是多少，右边是多少
    p = cond.value_counts()/cond.size
    
    indexs = p.index#True,False
    
    entropy = 0
    for index in indexs:
        user = X[cond ==index]['真实用户']#取出了目标值y的数据
        
        p_user = user.value_counts()/user.size
        #每个分支的信息熵
        entropy += (p_user*np.log2(1/p_user)).sum()*p[index]
    print(split,entropy)

归一化（Normalization）是数据预处理中的一种常用技术，它将数据的数值范围调整到一个特定的区间，通常是0到1之间，或者-1到1。归一化的目的和好处包括：

1. 统一尺度：不同特征的数值范围可能差异很大。归一化确保所有特征都在相同的尺度上，有助于算法更公平地对待每个特征。

2. 提高计算效率：某些算法在数值范围较小的情况下收敛得更快。

3. 避免数值问题：在数值计算中，非常大的数值可能导致计算精度问题或溢出。归一化可以减少这种风险。

4. 改善模型性能：对于基于梯度的优化算法（如神经网络），归一化可以加速收敛并提高模型性能。

5. 特征可比性：归一化后的特征可以更容易地进行比较和解释。

6. 算法要求：某些算法，如k-最近邻（k-NN）和主成分分析（PCA），对数据的尺度非常敏感，归一化可以提高这些算法的效果。

7. 概率解释：在处理概率分布或基于概率的算法时，归一化确保了概率的总和为1，这是概率论的一个基本要求。

8. 公平性：在多目标优化或多任务学习中，归一化可以帮助平衡不同目标或任务的重要性。

9. 兼容性：不同的数据源可能有不同的量纲和数值范围，归一化有助于将它们统一到一个可比较的标准。

10. 可视化：在数据可视化中，归一化可以帮助更清晰地展示数据的分布和关系。

归一化用于计算概率分布，这是为了确保在计算信息熵时，每个类别的概率之和为1，从而正确地反映数据的分布情况。