数据结构(5.5_2)——并查集

逻辑结构——数据元素之间的逻辑关系

并查集：

并查集（Union-Find）是一种树型的数据结构，用于处理一些不交集的合并及查询问题。它支持两种操作：

用双亲表示存储并查集 

首先将所有根节点数组值设为-1，其他结点数组值对应其父节点的数组下标

查找（Find）：

确定某个元素处于哪个子集，它可以用来确定两个元素是否属于同一个子集。

如何“查”到一个元素到底属于哪一个集合？

---从指定元素出发，一路向上，找到根结点---

如何判断两个元素到底是否属于同一个集合？

---分别查到两个元素的根，判断节点是否相同即可---

合并（Union）：

将两个子集合并成一个集合。

把两个集合“并“为一个集合

---让一棵树成为另一棵树的子树即可---

树的存储——双亲表示法(回忆)

并查集的代码实现

初始化

先将所有结点数组值设为-1

#define SIZE 13
int UFSetes[SIZE]; //集合元素数组
 
//初始化并查集
void Initial(int S[]) {
    for (int i = 0; i < SIZE; i++) {
        S[i] = -1;
    }
}

并、查

查操作：

//Find "查"操作，找x所属集合(返回x所属根结点)
int Find(int S[], int x) {
    while (S[x] >= 0)//循环寻找x的根
        x = S[x];
    return x;//根的S[]小于0
}

并操作：

 

//Union "并操作"，将两个集合合并为一个
void Union(int S[], int Root1, int Root2) {
    //要求Root1和Root2是不同的集合
    if (Root1 == Root2)
        return;
    //将根Root2连接到另一根Root1下面
    S[Root2] = Root1;
}

时间复杂度分析

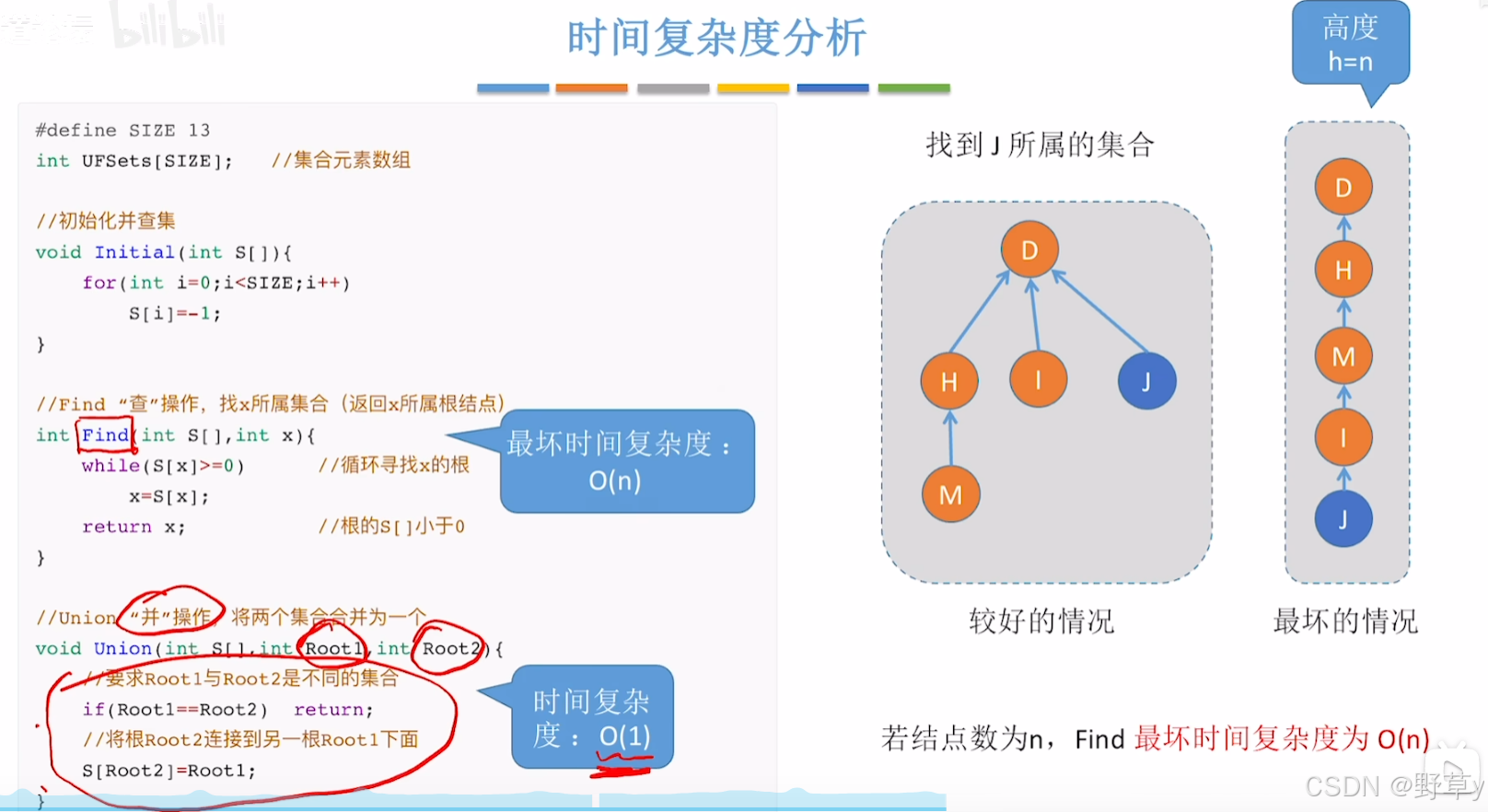
Union的优化操作 

优化思路：在每次Union操作构建树的时候，尽可能让树不长高

1. 用根节点的绝对值表示树的结点总数
2. Union操作，让小树合并到大树

 

代码：

//Union "并操作"，小树合并到大树
void Union(int S[], int Root1, int Root2) {
    if (Root1 == Root2)
        return;
    if (S[Root2] > S[Root1]) {//Root2结点数更少
        S[Root1] += S[Root2];//累加结点总数
        S[Root2] = Root1;//小树合并到大树
    }
    else {
        S[Root2] += S[Root1];//累加结点总数
        S[Root1] = Root2;//小树合并到大树
    }
}

总结：