力扣 240.搜素矩阵II

题目描述：

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

• 每行的元素从左到右升序排列。
• 每列的元素从上到下升序排列。

示例 1：

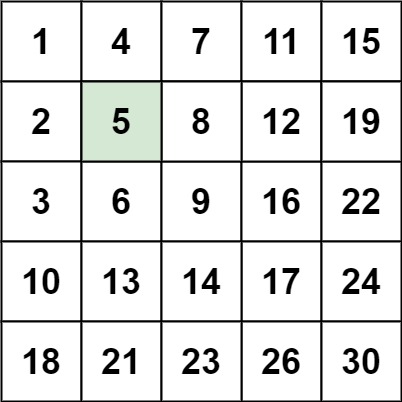
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

示例 2：

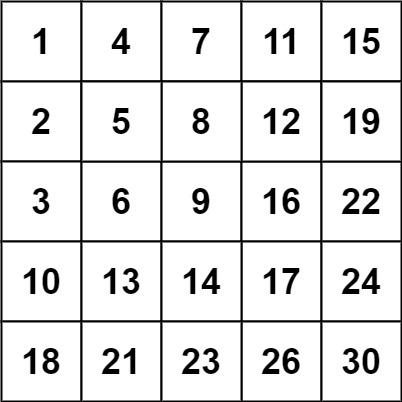
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

题解1：

比较巧妙的排除法，首先从矩阵的右上角开始找起，如果右上角元素x比target大，那么说明右上角这一列都不会存在target，因此这一列就不需要再遍历；如果x比target小，那么就说明，右上角这一行都不会存在target，排除这一行。

实现代码：

public static boolean searchMatrix2(int[][] matrix, int target) {
        int m  = matrix.length;//行数
        int n  = matrix[0].length;//列数
        int i  = 0 ;
        int j = n-1;
        while(i<m&&j>=0){
            if(matrix[i][j]==target){
                return true;
            }else if(matrix[i][j]>target){
                j--;
            }else{
                i++;
            }
        }
        return false;
    }

题解2：

 使用常规方法对每一行进行二分查找，看是否存在target

实现代码：

int m = matrix.length;
        int n = matrix[0].length;
        for (int i = 0; i < m; i++) {
            int l = 0;
            int r = n-1;
            while(l<=r){
                int mid = (r-l)/2+l;
                if(matrix[i][mid]==target){
                    return true;
                }else if(matrix[i][mid]>target){
                    r = mid-1;
                }else{
                    l = mid+1;
                }
            }
        }
        return false;