排序算法——归并排序以及非递归实现

一、归并排序思想

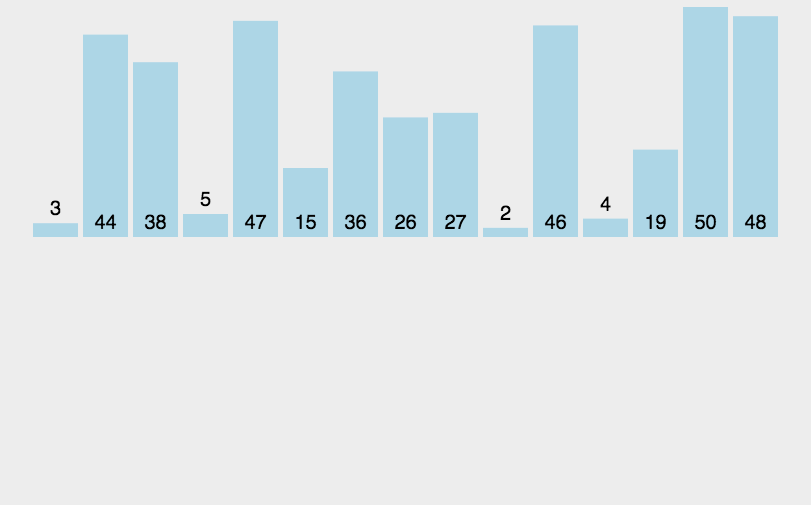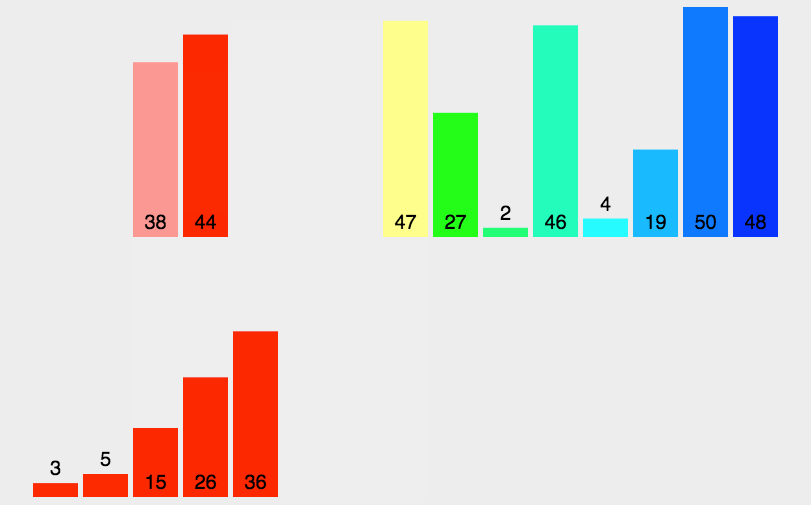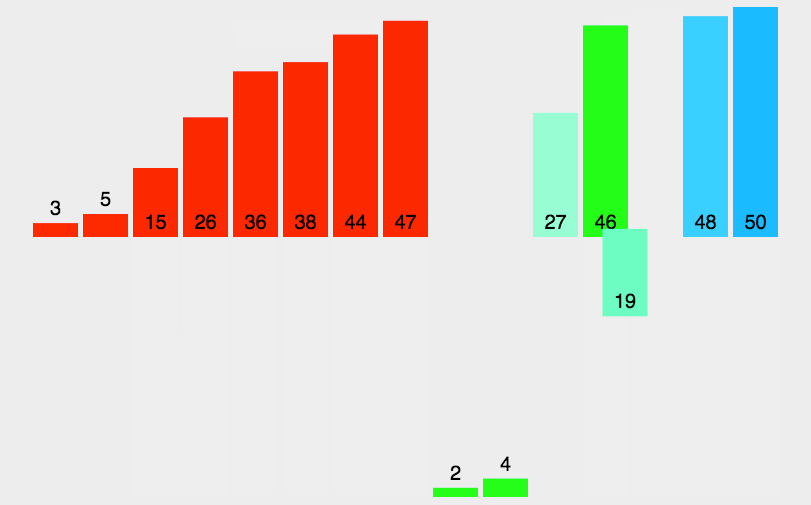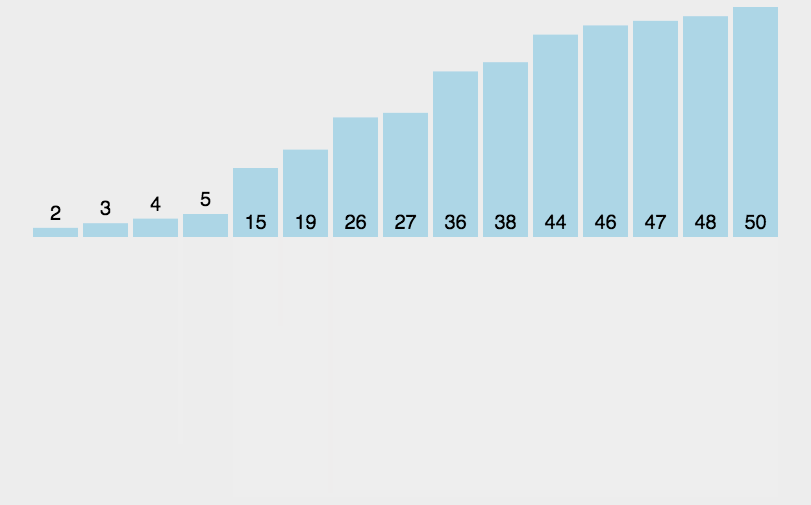
归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide andConquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。 归并排序核心步骤 ：

我们现在要树立这么一个思路，分解数组并不是真的分解数组，而是可以通过下标的形式来区分数组。归并排序实际上就是将一个数组分解到不能子啊分解的部分，两两经行比较排序，再将数据更新到新的数组中去。这非常类似于我们学的数的后序遍历。

二、代码实现

1、单趟：

我们先写单趟，因为归并排序是对半分组，所以最后为两个区间经行比较，思路转化为之前我们学过的两个数组的合并

int mid = (rigt + left) / 2;
int begin1 = left;
int end1 = mid-1;
int begin2 = mid;
int end2 = rigt;
int i = left;
while (begin1 <= end1 && begin2 <= end2)
{
 
	if (a[begin1] > a[begin2])
	{
		tmp[i++] = a[begin2++];
	}
	else
	{
		tmp[i++] = a[begin1++];
	}
}
while (begin1<=end1)
{
	tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
	tmp[i++] = a[begin2++];
}
memcpy(a+left, tmp+left, sizeof(int) * (rigt - left + 1));

这里要注意两个问题：1、区间怎么划分合适，2、为什么每排序一次就得将数组拷贝回去

 2、单趟问题解释

首先我们先解决第一个问题：区间怎么划分合适？

我们这里以下面图为例：

因为有-1的存在很容易导致下标为负数，最后导致数组的违法访问。同时可能还会有死循环的问题：

具体原因如下：

但是如果改为区间为 

int begin1 = left;
int end1 = mid;
int begin2 = mid+1;
int end2 = rigt;就不会出现这个问题：

所以正确代码如下：

int mid = (rigt + left) / 2;
int begin1 = left;
int end1 = mid;
int begin2 = mid+1;
int end2 = rigt;
int i = left;
while (begin1 <= end1 && begin2 <= end2)
{
 
	if (a[begin1] > a[begin2])
	{
		tmp[i++] = a[begin2++];
	}
	else
	{
		tmp[i++] = a[begin1++];
	}
}
while (begin1<=end1)
{
	tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
	tmp[i++] = a[begin2++];
}
memcpy(a+left, tmp+left, sizeof(int) * (rigt - left + 1));

第二个问题：因为比较的时候是在原数组经行比较如果不及时将数组内容更新，可能会导致再排序时经行错误的大小比较，最后导致结果错误 

3、总体代码实现

结束条件当分割区间等于1或者小于1的时候。

void _MergeSort(int* a, int* tmp, int left, int rigt)
{
	if (left >= rigt)
	{
		return;
	}
	int mid = (rigt + left) / 2;
	_MergeSort(a, tmp, left, mid);
	_MergeSort(a, tmp, mid + 1, rigt);
	int begin1 = left;
	int end1 = mid;
	int begin2 = mid+1;
	int end2 = rigt;
	int i = left;
	while (begin1 <= end1 && begin2 <= end2)
	{
 
		if (a[begin1] > a[begin2])
		{
			tmp[i++] = a[begin2++];
		}
		else
		{
			tmp[i++] = a[begin1++];
		}
	}
	while (begin1<=end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}
	memcpy(a+left, tmp+left, sizeof(int) * (rigt - left + 1));
}
void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		return;
	}
	else
	{
		_MergeSort(a, tmp, 0, n - 1);
		free(tmp);
		tmp = NULL;
	}
}

三、非递归

对于归并排序我们实现非递归用循环更好一点，非递归我们可以直接从递归回去那出发，定义一个组个数，通过控制组的个数实现“并”这个过程：

还是我们先写一个数组只有一个数的情况：

for (int i = 0; i < end - begin + 1; i += 2 * gap)//每次比较两组，所以加2gap
{
	int begin1 = i;
	int end1 = begin1 + gap - 1;
	int begin2 = begin1 + 2 * gap - 1;//第二组的开头与第一组的开头差2倍
	int end2 = begin2 + gap - 1;
	int k = i;
	while (begin1 <= end1 && begin2 <= end2)
	{
 
		if (a[begin1] > a[begin2])
		{
			tmp[k++] = a[begin2++];
		}
		else
		{
			tmp[k++] = a[begin1++];
		}
	}
	while (begin1 <= end1)
	{
		tmp[k++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[k++] = a[begin2++];
	}
	memcpy(a + i, tmp + i, sizeof(int) * (2 * gap));//同理这里也得排序一次就拷贝回去
 
}

那么后面就是gap*2控制即可：

void _MergeSortNonR(int* a, int* tmp,int begin, int end)
{
	int gap = 1;
	for (int j = gap; j < end-begin+1; j *= 2)
	{
		for (int i = 0; i < end - begin + 1; i += 2 * gap)//每次比较两组，所以加2gap
		{
			int begin1 = i;
			int end1 = begin1 + gap - 1;
			int begin2 = begin1 + 2 * gap - 1;//第二组的开头与第一组的开头差2倍
			int end2 = begin2 + gap - 1;
			int k = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
 
				if (a[begin1] > a[begin2])
				{
					tmp[k++] = a[begin2++];
				}
				else
				{
					tmp[k++] = a[begin1++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[k++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[k++] = a[begin2++];
			}
			memcpy(a + i, tmp + i, sizeof(int) * (2 * gap));
		}
	}
}

但是上面的代码仍然存在问题，和快排类似这里会存在数组越界问题：这里我们打印数组下标区间来观察一下：、

大致我们可以分为这两种情况：

 如果end1越界，那么说明分为了只有这一组数据，不用排了直接跳出循环，如果end2越界我们就需要给end2修改值。

所以改进代码如下：

void _MergeSortNonR(int* a, int* tmp,int begin, int end)
{
	int gap = 1;
	for (int j = gap; j < end-begin+1; j *= 2)
	{
		for (int i = 0; i < end - begin + 1; i += 2 * gap)//每次比较两组，所以加2gap
		{
			int begin1 = i;
			int end1 = begin1 + gap - 1;
			int begin2 = begin1 + 2 * gap - 1;//第二组的开头与第一组的开头差2倍
			int end2 = begin2 + gap - 1;
			int k = i;
			// 第二组都越界不存在，这一组就不需要归并
			if (begin2 >= end - begin + 1)
				break;
 
			// 第二的组begin2没越界，end2越界了，需要修正一下，继续归并
			if (end2 >= end - begin + 1)
				end2 = end - begin + 1 - 1;
			while (begin1 <= end1 && begin2 <= end2)
			{
 
				if (a[begin1] > a[begin2])
				{
					tmp[k++] = a[begin2++];
				}
				else
				{
					tmp[k++] = a[begin1++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[k++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[k++] = a[begin2++];
			}
			memcpy(a + i, tmp + i, sizeof(int) * (2 * gap));
		}
	}
}
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		return;
	}
	else
	{
		_MergeSortNonR(a, tmp, 0, n - 1);
		free(tmp);
		tmp = NULL;
	}
}

可能有人会想如果只剩一组数据了，我直接return行不行？实际上是可以的，因为break跳出循环后在gap*2还是只有一组数据，所以直接return即可。