决策树算法的一点基础知识补充

熵

1948年，香农提出“信息熵”的概念。一条信息的信息量大小和他的不确定性有直接的关系，要搞清楚意见不确定的事，需要了解大量的信息。

熵用于表示随机变量的不确定性的度量，如果熵越大表示不确定性越大。

定义：用来度量信息的不确定程度

熵越大，信息量越大

不确定程度越低，熵越小。比如“明天太阳从东边升起”这句话的熵为0，因为这句话没有带有任何信息，他描述的事一个事实。

概率

改了就是用数值来标识某件事发生的可能性

当知道了概率这个数值，就代表着可以预测未来，因为能通过概率来判断出那种情况发生的可能性最大。

由于硬币只有两面，也就是说落地后只会有两种结果（立起来当我没说），要么正面朝上，要么反面朝上，所以抛硬币正面朝上的可能性用数值来表示，概率就是50%

概率的值永远在0-1范围之内，如果某件事不可能发生，则其概率为0，对应的就是这条直线上最左端的位置。如果某件事肯定会发送，则其概率为1，对应的就是这条直线上最右端的位置，也就是那个点赞的大拇指。大多数时候，所面临的都是介于0和1之间的概率事件。

比如这条直线上更靠近左端的投骰子，某一面数值朝上的概率是六分之一，处于中间位置的是抛硬币，正面或反面朝上的概率都是二分之一；靠近有段的从四个蓝色球、一个红色球里边，随机拿出四个蓝色球，正好都是蓝色球的概率是四分之五。

在统计概率中用事件表示某件事情，例如刚才投骰子正面朝上数值为1就是一个事件。在一定条件下，可能发生，可能不发生的事件叫做随机事件。例如投骰子就是一个随机事件。

信息量

信息量是确定一个随机事件所需要的信息度量。信息论鼻祖香农认为：信息是用以消除随机不确定性的东西。

举个栗子，竞猜世界杯32支队伍谁会夺冠？

1. 开始时假设对每个球队都不了解，那么就会认为所有队伍的夺冠概率十一月的，都是三十二分之一
2. 但是一旦获取了一些信息，比如通过查看历届的世界杯冠军，发现只有欧洲和南美的球队夺冠。

通过这个信息就能消除一些不确定性，将其他州的球队都排除

那么可能就剩下10支队伍，猜中的概率就变成了十分之一。

由此可知：信息确实能够降低随机事件的不确定性。那么想要确定出不确定性大的事件所需的信息就越多。因此就可以用所需的信息大小来度量事件的不确定性。而通常使用概率来表示事件的不确定性，即事件发生的概率越小，不确定性就越大。

我们就可以得到一个结论：

信息量越大 -> 事件不确定性越小；

使用概率表示事件的不确定性：

概率越大 -> 不确定性越小

根据以上推论，事件发生的概率p和事件的信息量I之间是呈现反比关系的，给出计算公式为：

那么为什么是上述的公式形式呢？有下面几点解释：

• 为什么用对数函数而不是其他函数？
  1. 为例满足一个基本的假设，对于两个不想管的事件X和Y，两者的信息量应为各自信息量之和，即I( X, Y ) = I( X ) + I( Y )。而概率应满足p(X, Y) = P( X ) * P( Y )。因此只有对数函数能够同时实现上述的变换，而底数2则是习惯操作，取其他数也是可以的。
• 为什么取负号？
  1. I和P之间呈现反比关系，且P ∈ [0, 1]，为了保证信息量为正数，因此取负号。当p = 0，即不可能发送事件，那么信息量为无穷大；当p = 1时，为确定事件，信息量最小为0；

人话：取值范围小于1，必然是负数，所以要加负号

• 扩展【何为对数】
  1. 若ab = N(a > 0, a ≠ 1)，则b叫做以a为底N的对数，记作b=logaN。当a = 10时称作常用对数，当a=e时称作自然对数。

熵

英文里的熵是希腊语“变化”的意思，中文的熵是一个生造字，胡刚教授翻译时灵机一动，把商字加火字旁来意译这个词

熵是随机事件所有可能结果信息量的加权平均值：每个事件的概率P与信息量I乘积之和，那么其表达式就是：

举个栗子

根据过去21届世界杯的历史冠军，计算各个球队夺得冠军的概率和信息量如下：

信息熵计算公式为：

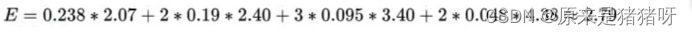
那么最终世界杯历史夺冠这个事件的信息熵就是2.79.此外，当事件的概率分布越均匀时，信息熵就会越大；而越集中，则信息熵也越大。（熵的单位是比特）

当随机变量X只有0、1两种取值，则又：H(X) = -plog(p) - (1-p)log(1-p)，可以画出一个二维坐标表表示他们的关系：

从而可知，当p=0.5时，熵取值最大，随机变量不确定性最大。

条件熵

定义

在一个条件下，随机变量的不确定性。

设有随机变量（X, Y），其联合概率分布为：

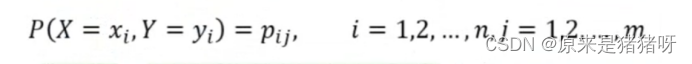
条件熵H(Y|X)表示在已知随机变量X的条件下，随机变量Y的不确定性。随机变量X给定的条件下随机变量Y的条件熵H(Y|X)定义为：X给定条件下Y的概率分布的熵对X的数学期望：

信息增量

信息增量表示的是：得知特征X的信息而使得分类Y的信息的不确定性减少的程度。如果某个特征的信息增益比较大，就表示该特征对结果的影响较大。特征A对数据集D的信息增量表示为：gain(A) = H(D) - H(D|A)

信息增益 = 熵 - 条件熵

信息增益的定义：在一个条件下，信息不确定性减少的程度

简单来说信息增量，就是当我们接收到新的信息时，这个信息给我们带来了多少“额外”的知识或认知上的变化。这里的“额外”是指与我们之前已知的信息相比较而言。

通俗地解释：

假设你正在看天气预报，之前的预报告诉你今天可能会下雨，但概率不是很高。但就在你准备出门前，你看到了最新的天气预报，这次它明确告诉你，由于突然出现的强冷空气，今天下雨的概率已经上升到了90%。

这里，新的天气预报信息给你带来了一个很大的“变化”或“增量”：你原来只知道可能会下雨，但现在你知道下雨的可能性非常高。这个变化的部分，即新信息给你带来的对事物认知上的额外增加，就是信息增量。

所以，信息增量其实就是新信息给我们带来的对事物认知上的额外增加或改变。

ID3算法

概念：ID3算法是一种贪心算法，用于构造决策树。它起源于概念学习系统(CLS)，并使用信息熵的下降速度作为选取测试属性的标准。

原理：

①信息熵：信息熵是衡量数据集混乱程度（或不确定性）的一个指标。当数据集中的样本全部属于同一类别时，信息熵最小（为0），表示数据集最纯净、最确定；反之，如果数据集中的样本均匀分布在不同的类别中，信息熵最大，表示数据集最混乱、最不确定。

②信息增益：信息增益是衡量某个特征对于减少数据集不确定性的贡献。具体地，ID3算法会计算每个特征的信息增益，然后选择具有最高信息增益的特征作为当前节点的划分特征。

③递归构建：根据选择的划分特征，ID3算法将数据集划分成多个子集，并对每个子集递归地应用ID3算法，直到满足停止条件（如所有样本都属于同一类别、没有更多的特征可用于划分、达到预定的树深度等）。

特点：ID3算法倾向于选择取值较多的特征，因为它会给予这些特征更高的信息增益。然而，这可能导致决策树过于复杂，并产生过拟合。

C4.5算法

概念：C4.5是ID3算法的一个改进版本，它使用信息增益率来选择属性。

原理：

①信息增益率：信息增益率是在信息增益的基础上加入了一个分裂信息度量，用于平衡取值较多的特征。这有助于避免ID3算法中过于倾向选择取值较多特征的问题。

②其他特性：C4.5算法能够处理非离散数据和缺失值，并可以对非完整数据进行处理。

特点：C4.5算法通过引入信息增益率，改进了ID3算法在选择属性时的偏向性，并增加了对非离散数据和缺失值的处理能力。

CART算法

概念：CART算法（Classification And Regression Tree）既可以用于创建分类树，也可以用于创建回归树。

原理：

①基尼系数：CART分类树算法使用基尼系数作为选择特征的标准。基尼系数越小，表示模型的不纯度越低，特征越好。

②二分法：CART算法每次仅对某个特征的值进行二分，而不是多分，因此CART算法构建的决策树是二叉树。

特点：CART算法既可以处理分类问题，也可以处理回归问题，并且构建的决策树是二叉树，结构相对简洁。

ID3、C4.5和CART是三种不同的决策树算法，它们在选择特征和构建决策树的过程中各有特点。ID3算法基于信息增益，C4.5算法基于信息增益率，而CART算法则基于基尼系数和二分法。