【线性代数 & C++】结合逆矩阵的克拉默法则

1 原理

对于$n$个变量、$n$个方程的线性方程组$$\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1n}{x}_n=b_1\\ a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2n}{x}_n=b_2\\ \cdots \cdots \cdots \\ a_{n1}{x}_1+a_{n2}{x}_2+\cdots +a_{nn}{x}_n=b_n\end{array},\text{\hspace{1em}(1)}$$如果它的系数行列式$D\ne 0$，则它有唯一解.

• 把方程组(1)写成矩阵方程$$Ax=b,\text{\hspace{1em}(2)}$$因$\left|\begin{array}{c}A\end{array}\right|\ne 0$，故$A^{-1}$存在.
• 方程(2)可以变换为$$A^{-1}Ax=Ex=x=A^{-1}b.\text{\hspace{1em}(3)}$$
• 即$$x=A^{-1}b.$$

2 C++实现

• 采用新方法对博文【线性代数｜C++】克拉默法则的中测试案例进行再计算.

//test.cpp文件
#include 
#include 
#include 

#include "CMatrix.h"

using namespace std;

bool PrintMat
(
  const vector<vector<double>> &vvMat
)
{
  for (int i = 0; i < vvMat.size(); i++)
  {
    for (int j = 0; j < vvMat[i].size(); j++)
    {
      cout << setw(5) << vvMat[i][j];
    }
    cout << endl;
  }
  
  return true;
}

int main()
{
    //系数阵
    vector<vector<double>> vvMatA{{ 2, 1,-5, 1},
                                  { 1,-3, 0,-6},
                                  { 0, 2,-1, 2},
                                  { 1, 4,-7, 6}};
    
    vector<vector<double>> vvMatb{{8}, {9},{-5}, {0}};//常数阵
    vector<vector<double>> vvMatTemp;//存储逆矩阵
    vector<vector<double>> vvMatRet;//存储方程解的矩阵
    
    //求逆矩阵
    if (false == CMatrix::GetInverseMat(vvMatA, vvMatTemp))
    {
        cout << "计算失败" << endl;
    }
    else
    {
        //逆矩阵与常数阵相乘
        if (false == CMatrix::MatMulti(vvMatTemp, vvMatb, vvMatRet))
        {
            cout << "计算失败" << endl;
        }
        else
        {
            PrintMat(vvMatRet);
        }
    } 

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

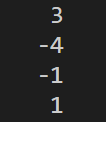
• 两种计算方法结果一致。

---

1. 引用文献：《工程数学 线性代数（第五版）》同济大学数学系编,高等教育出版社
2. 以上为个人学习、练习的记录，如有错误，欢迎指正。