• 机器学习（三）之监督学习2

    前言：

    本专栏一直在更新机器学习的内容，欢迎点赞收藏哦！

    笔者水平有限，文中掺杂着自己的理解和感悟，如果有错误之处还请指出，可以在评论区一起探讨！

     1.支持向量机（Support Vector Machines，简称SVM）

    1.1 前言

    概念：

    支持向量机（support vector machines, SVM）是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机

    引入：

    上一篇讲KRR时，我们也提到了一点SVM。在这一节中我们详细的说明一下这种方法。

    优势：

    1. 对高维空间有效
    2. 当维度比样本数量大时还有效
    3. 使用训练集的子集，空间内存使用较少
    4. 具有通用性，可以指定不同的核函数

    缺点：

    1. 如果维度比样本数量大很多时，注意避免过拟合。可以选择合适的核函数和正则化项（惩罚项）
    2. 不直接提供概率估计

    1.2 分类

    主要是三种分类算法：SVC(C-Support Vector Classification),NuSVC(Nu-Support Vector Classification)和LinearSVC(Linear Support Vector Classification)。我们就简单的来看一下，区别和使用方法。

    区别：

    SVC和NuSVC方法基本一致，唯一区别就是损失函数的度量方式不同。

     • NuSVC中的nu参数（训练误差部分的上限和⽀持向量部分的下限，取值在(0，1)之间，默认是0.5）和SVC中的C参数（c越等于0，惩罚越大，准确率高，但容易过拟合）;

     • LinearSVC是实现线性核函数的支持向量分类，没有kernel参数。

    SVC代码：

    1. import numpy as np
    2. from sklearn.svm import SVC
    3. from sklearn.pipeline import make_pipeline
    4. import matplotlib.pyplot as plt
    5. from sklearn.preprocessing import StandardScaler
    6.  
    7. x = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
    8. y = np.array([1, 1, 2, 2])
    9. clf = make_pipeline(StandardScaler(), SVC(gamma='auto'))
    10. clf.fit(x, y)
    11. x_test = np.array([[-0.8, -1]])
    12.  
    13. y_test = clf.predict(x_test)
    14. x_line = np.linspace(-2, 2, 100)
    15.  
    16. # 绘制训练集数据点
    17. plt.scatter(x[:, 0], x[:, 1], c=y, cmap=plt.cm.Paired, label='Training Points')
    18.  
    19. # 绘制决策边界
    20. x_min, x_max = x[:, 0].min() - 1, x[:, 0].max() + 1
    21. y_min, y_max = x[:, 1].min() - 1, x[:, 1].max() + 1
    22. xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100), np.linspace(y_min, y_max, 100))  # 生成了一个二维的网格点坐标矩阵
    23. Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])  # 预测坐标范围内每个点的类别
    24. Z = Z.reshape(xx.shape)
    25. plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8)  # cmap=plt.cm.Paired 指定了等高线的颜色映射
    26.  
    27. # 绘制测试点
    28. plt.scatter(x_test[:, 0], x_test[:, 1], c='red', marker='x', label='Test Point')
    29.  
    30. plt.xlabel('Feature 1')
    31. plt.ylabel('Feature 2')
    32. plt.title('SVM Classification')
    33. plt.legend()
    34. plt.show()

     NuSVC代码：

    1. import numpy as np
    2. from sklearn.svm import SVC,NuSVC
    3. from sklearn.pipeline import make_pipeline
    4. import matplotlib.pyplot as plt
    5. from sklearn.preprocessing import StandardScaler
    6.  
    7. x = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
    8. y = np.array([1, 1, 2, 2])
    9. clf = make_pipeline(StandardScaler(), NuSVC())
    10. clf.fit(x, y)
    11. x_test = np.array([[-0.8, -1]])
    12.  
    13. y_test = clf.predict(x_test)
    14. x_line = np.linspace(-2, 2, 100)
    15.  
    16. # 绘制训练集数据点
    17. plt.scatter(x[:, 0], x[:, 1], c=y, cmap=plt.cm.Paired, label='Training Points')
    18.  
    19. # 绘制决策边界
    20. x_min, x_max = x[:, 0].min() - 1, x[:, 0].max() + 1
    21. y_min, y_max = x[:, 1].min() - 1, x[:, 1].max() + 1
    22. xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100), np.linspace(y_min, y_max, 100))  # 生成了一个二维的网格点坐标矩阵
    23. Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])  # 预测坐标范围内每个点的类别
    24. Z = Z.reshape(xx.shape)
    25. plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8)  # cmap=plt.cm.Paired 指定了等高线的颜色映射
    26.  
    27. # 绘制测试点
    28. plt.scatter(x_test[:, 0], x_test[:, 1], c='red', marker='x', label='Test Point')
    29.  
    30. plt.xlabel('Feature 1')
    31. plt.ylabel('Feature 2')
    32. plt.title('NuSVC Classification')
    33. plt.legend()
    34. plt.show()

     LinearSVC代码：

    1. import numpy as np
    2. from sklearn.svm import LinearSVC
    3. from sklearn.pipeline import make_pipeline
    4. from sklearn.preprocessing import StandardScaler
    5. from sklearn.datasets import make_classification
    6. import matplotlib.pyplot as plt
    7.  
    8. X, y = make_classification(n_features=4, random_state=0)  #随机生成样本
    9. clf = make_pipeline(StandardScaler(),LinearSVC(dual="auto", random_state=0, tol=1e-5))
    10.  
    11. clf.fit(X,y)
    12. coef=clf.named_steps['linearsvc'].coef_
    13. intercept=clf.named_steps['linearsvc'].intercept_
    14. x_test=np.array([[0,0,0,0]])
    15. y_test=clf.predict(x_test)
    16. from sklearn.decomposition import PCA
    17.  
    18. # 将数据投影到二维平面
    19. pca = PCA(n_components=2)
    20. X_pca = pca.fit_transform(X)
    21.  
    22. # 训练 LinearSVC
    23. clf.fit(X_pca, y)
    24. # 投影测试点到二维空间
    25. x_test_pca = pca.transform(x_test)
    26.  
    27. # 绘制样本点
    28. plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap=plt.cm.Paired)
    29.  
    30. # 绘制决策边界
    31.  
    32.  
    33. # 绘制测试点
    34. plt.scatter(x_test_pca[:, 0], x_test_pca[:, 1], c='red', marker='x', label='Test Point')
    35. # 获取系数和截距
    36. coef = clf.named_steps['linearsvc'].coef_
    37. intercept = clf.named_steps['linearsvc'].intercept_
    38.  
    39. # 绘制样本点
    40. plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap=plt.cm.Paired)
    41.  
    42. # 绘制决策边界
    43. x_min, x_max = X_pca[:, 0].min() - 1, X_pca[:, 0].max() + 1
    44. y_min, y_max = X_pca[:, 1].min() - 1, X_pca[:, 1].max() + 1
    45. xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
    46.                      np.arange(y_min, y_max, 0.02))
    47. Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    48. Z = Z.reshape(xx.shape)
    49. plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8)
    50.  
    51. plt.xlabel('Principal Component 1')
    52. plt.ylabel('Principal Component 2')
    53. plt.title('Linear SVM Decision Boundary (PCA)')
    54. plt.show()

     这一部分不好画在二维图片上，我们使用了PCA降维技术，降维到平面上再显现在二维平面上的。相当于降维之后又训练了一遍，才能画出来的。

    总结：

    • 数据线性可分，或者需要一个训练速度更快的模型，那么可以选择LinearSVC
    • 处理非线性问题，可以尝试使用SVC，并尝试不同的核函数
    • 想要一个介于SVC和LinearSVC之间的模型，你可以尝试使用NuSVC

    1.3 回归

    分为：SVR,NuSVR,LinearSVR。

    方法和上面差不多，我们就不多讲了。

    1.4 复杂度

    和之间

    1.5 使用提示

    1. 避免数据拷贝：SVC、SVR、NuSVC和NuSVR如果不按照特定方法输入，数据就会被拷贝一份。LinearSVC和LogisticRegression任何numpy数组输入都会被拷贝。如果是大规模线性分类器且不想拷贝数据，可以使用SGDC.
    2. 核缓存大小：对SVC、SVR、NuSVC和NuSVR，核缓存的大小对较大问题求解的运行时间有非常强的影响，如果你有足够内存，建议将cache_size设置为一个高于默认值200（MB）的值，比如500（MB）或1000（MB）。
    3. 设置C：默认情况下C设为1，这是一个合理的选择。如果样本中有许多噪音观察点，则应该减小这个值。这意味着对估计结果进行更严格的正则化。
    4. SVM算法会受数据取值范围的影响，所以强烈建议在使用之前对数据进行缩放

     1.6 核方法

     2.随机梯度下降算法（Stochastic Gradient Descent）

    2.1 前言

    优点：

    • 高效
    • 易于实现

    缺点：

    • 需要调参
    • 对特征缩放非常敏感

    警告：

    在拟合数据之前一定要打乱训练数据（shuffle=True）并进行标准化（make_pipeline(StandardScaler(), SGDClassifier())） 

    梯度下降和随机梯度下降的区别：

    梯度下降（Gradient Descent）：

    • 在梯度下降中，每次迭代都使用全部训练数据来计算损失函数的梯度，并更新模型参数。
    • 因为每次迭代都需要对整个数据集进行操作，所以在大数据集上训练时，梯度下降的计算开销会很大。
    • 梯度下降通常用于批量学习（Batch Learning）的情况下，其中数据集可以完全载入内存。

     随机梯度下降（Stochastic Gradient Descent，SGD）：

    • 在随机梯度下降中，每次迭代只使用一个样本（或一小批样本）来计算损失函数的梯度，并更新模型参数。
    • 因为每次迭代只需要处理一个样本（或一小批样本），所以SGD的计算开销较小，特别适合于大数据集和在线学习（Online Learning）的场景。
    • 由于每次迭代只使用部分样本计算梯度，SGD的更新过程可能会更加不稳定，但同时也可能更快地找到局部最优解。

     小批量梯度下降（Mini-batch Gradient Descent）：

    • 除了梯度下降和随机梯度下降外，还存在一种折中的方法，即小批量梯度下降。在每次迭代中，它使用一个小批量的样本来计算梯度。
    • 小批量梯度下降结合了梯度下降和SGD的优点，既可以利用并行计算加速训练，又不会因为单一样本的噪声导致更新过于不稳定

     总结：

    GD和SGD主要区别为训练过程中使用的样本数量不同，GD需要大开销，SGD不稳定。

    2.2 原理：

    主要是通过计算样本的损失函数，迭代更新模型参数。让这个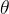\theta不断变换（如下图公式），直到达到最大迭代次数或者损失函数收敛到某个值以内。

     误差函数有很多种可以按需挑选。

     2.3 复杂度

     2.4 使用提示

    1. 对数据进行缩放：将输入向量X上的每个特征缩放为[0，1]或[-1，+1]，或将其标准化为均值为0和方差为1
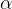    2. 找到合理的\alpha学习率
    3. SGD在观察了大约10^6个训练样本后收敛
    4. 如果将SGD应用于PCA提取的特征，通常明智的做法是将特征值通过某个常数c缩放，使训练数据的L2范数平均值等于1。
    5. 当特征很多或 eta0 很大时， ASGD（平均随机梯度下降） 效果更好。

    先写这么多监督算法，后面再慢慢补充，可能还会补充朴素贝叶斯和决策树、特征选择。

    大家可以先点赞关注，以后慢慢看哦！

  • 相关阅读:
    NVIDIA CUDA Win10安装步骤
    计算机网络 期末复习（谢希仁版本）第3章
    join on后面 加条件 与 where后面加条件的区别
    vue3解决报错：ResizeObserver loop completed with undelivered notifications
    java泛型
    先睹为快_Mandelbrot集
    2毛钱不到的2A同步降压DCDC电压6V频率1.5MHz电感2.2uH封装SOT23-5芯片MT3520B
    硬盘驱动器（HDD）伺服系统鲁棒控制
    数值常量如何转化为内存地址？
    元年专利解析｜元数据管理系统和使用其对模型对象进行建模的方法
  • 原文地址：https://blog.csdn.net/weixin_75205835/article/details/138070419