• 偏微分方程算法之二阶双曲型方程交替方向隐格式

    目录

    一、研究目标

    二、理论推导

    2.1 显差分格式

    2.2 交替方向隐格式

    三、算例实现

    四、结论

    一、研究目标

            本节的研究对象为如下的双曲型偏微分方程初边值问题：

    \left\{\begin{matrix} \frac{\partial^{2}u(x,y,t)}{\partial t^{2}}-(\frac{\partial^{2}u(x,y,t)}{\partial x^{2}}+\frac{\partial^{2}u(x,y,t)}{\partial y^{2}})=f(x,y,t),(x,y)\in \Omega=[0,a]\times [0,b],0<t\leqslant T,\\ u(x,y,0)=\varphi(x,y),\frac{\partial u}{\partial t}(x,y,0)=\Psi(x,y),(x,y)\in \Omega \space\space\space\space(1),\\ u(0,y,t)=g_{1}(y,t),u(a,y,t)=g_{2}(y,t),0\leqslant y \leqslant b,0<t\leqslant T,\\ u(x,0,t)=g_{3}(x,t),u(x,b,t)=g_{4}(x,t),0\leqslant x \leqslant a,0<t \leqslant T \end{matrix}\right.

            为了保证连续性，公式（1）中相关函数满足：

    g_{1}(0,t)=g_{3}(0,t),g_{1}(b,t)=g_{4}(b,t)\\g_{2}(0,t)=g_{3}(a,t),g_{2}(b,t)=g_{4}(a,t)

    \varphi(0,y)=g_{1}(y,0),\varphi(a,y)=g_{2}(y,0)\\\varphi(x,0)=g_{3}(x,0),\varphi(x,b)=g_{4}(x,0)

    二、理论推导

    2.1 显差分格式

            第一步：网格剖分。在三维长方体空间（二维平面加一维时间轴）进行网格剖分，将区域[0,a]等分m份，区域[0,b]等分n份，区域[0,T]等分l份，即

    x_{i}=i\cdot\Delta x=\frac{ia}{m},0\leqslant i\leqslant m,y_{j}=j\cdot\Delta y=\frac{jb}{n},0\leqslant j\leqslant n,t_{k}=k\cdot\Delta t=\frac{kT}{l},0\leqslant k\leqslant l

    得到网格节点坐标为(x_{i},y_{j},t_{k})。我们利用数值方法获得精确解u(x,y,t)在网格节点(x_{i},y_{j},t_{k})处的近似值，即数值解u^{k}_{i,j}。

            第二步：弱化原方程，仅在离散点处成立。即

    \left\{\begin{matrix} \frac{\partial^{2}u}{\partial t^{2}}|_{(x_{i},y_{j},t_{k})}-(\frac{\partial^{2}u}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}})|_{(x_{i},y_{j},t_{k})}=f(x_{i},y_{j},t_{k}),0\leqslant i\leqslant m,0\leqslant j\leqslant n,0<k\leqslant l,\\ u(x_{i},y_{j},t_{0})=\varphi(x_{i},y_{j}),\frac{\partial u}{\partial t}(x_{i},y_{j},t_{0})=\Psi(x_{i},y_{j}),0\leqslant i\leqslant m,0\leqslant j\leqslant n,\space\space(2)\\ u(x_{0},y_{j},t_{k})=g_{1}(y_{j},t_{k}),u(x_{m},y_{j},t_{k})=g_{2}(y_{j},t_{k}),0\leqslant j\leqslant n,0<k\leqslant l,\\ u(x_{i},y_{0},t_{k})=g_{3}(x_{i},t_{k}),u(x_{i},y_{n},t_{k})=g_{4}(x_{i},t_{k}),0\leqslant i\leqslant m,0<k\leqslant l \end{matrix}\right.

            第三步：差商代替微商处理偏导数。方程组二阶偏导数使用中心差商来近似，即

    \frac{\partial^{2}u}{\partial t^{2}}|_{(x_{i},y_{j},t_{k})}\approx\frac{u(x_{i},y_{j},t_{k-1})-2u(x_{i},y_{j},t_{k})+u(x_{i},y_{j},t_{k+1})}{\Delta t^{2}}

    \frac{\partial^{2}u}{\partial x^{2}}|_{(x_{i},y_{j},t_{k})}\approx\frac{u(x_{i-1},y_{j},t_{k})-2u(x_{i},y_{j},t_{k})+u(x_{i+1},y_{j},t_{k})}{\Delta x^{2}}

    \frac{\partial^{2}u}{\partial y^{2}}|_{(x_{i},y_{j},t_{k})}\approx\frac{u(x_{i},y_{j-1},t_{k})-2u(x_{i},y_{j},t_{k})+u(x_{i},y_{j+1},t_{k})}{\Delta y^{2}}

    对于初始条件中的一阶偏导数，也采用二阶中心差商，即

    \frac{\partial u}{\partial t}|_{(x_{i},y_{j},t_{k})}\approx\frac{u(x_{i},y_{j},t_{1})-u(x_{i},y_{j},t_{-1})}{2\Delta t}

            将差商公式带入公式（2），用数值解代替精确解并忽略高阶项，可得对应的数值格式为

    \left\{\begin{matrix} \frac{u^{k-1}_{i,j}-2u^{k}_{i,j}+u^{k+1}_{i,j}}{\Delta t^{2}}-(\frac{u^{k}_{i-1,j}-2u^{k}_{i,j}+u^{k}_{i+1,j}}{\Delta x^{2}}+\frac{u^{k}_{i,j-1}-2u^{k}_{i,j}+u^{k}_{i,j+1}}{\Delta y^{2}})=f(x_{i},y_{j},t_{k}),1\leqslant i\leqslant m-1,1\leqslant j\leqslant n-1,1\leqslant k\leqslant l-1,\\ u^{0}_{i,j}=\varphi(x_{i},y_{j}),u^{1}_{i,j}=u^{-1}_{i,j}+2\Delta t\Psi(x_{i},y_{j}),0\leqslant i\leqslant m,0\leqslant j\leqslant n,\space\space(3)\\ u^{k}_{0,j}=g_{1}(y_{j},t_{k}),u^{k}_{m,j}=g_{2}(y_{j},t_{k}),0\leqslant j\leqslant n,0<k\leqslant l,\\ u^{k}_{i,0}=g_{3}(x_{i},t_{k}),u^{k}_{i,n}=g_{4}(x_{i},t_{k}),0\leqslant i\leqslant m,0<k\leqslant l \end{matrix}\right.

            为消去虚拟边界项u^{-1}_{i,j}，让公式（3）中第1式对k=0成立，可得

    \frac{u^{-1}_{i,j}-2u^{0}_{i,j}+u^{1}_{i,j}}{\Delta t^{2}}-(\frac{u^{0}_{i-1,j}-2u^{0}_{i,j}+u^{0}_{i+1,j}}{\Delta x^{2}}+\frac{u^{0}_{i,j-1}-2u^{0}_{i,j}+u^{0}_{i,j+1}}{\Delta y^{2}})=f(x_{i},y_{j},t_{0})

            再结合公式（3）中第3式中越界的u^{-1}_{i,j}=u^{1}_{i,j}-2\Delta t\Psi(x_{i},y_{j})，消去虚拟边界项u^{-1}_{i,j}，可得

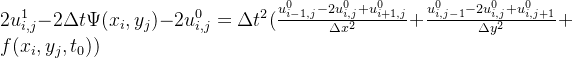
    2u^{1}_{i,j}-2\Delta t\Psi(x_{i},y_{j})-2u^{0}_{i,j}=\Delta t^{2}(\frac{u^{0}_{i-1,j}-2u^{0}_{i,j}+u^{0}_{i+1,j}}{\Delta x^{2}}+\frac{u^{0}_{i,j-1}-2u^{0}_{i,j}+u^{0}_{i,j+1}}{\Delta y^{2}}+f(x_{i},y_{j},t_{0}))

    记r_{1}=\Delta t^{2}/\Delta x^{2}, r_{2}=\Delta t^{2}/\Delta y^{2}，整理上式可得

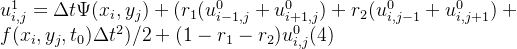
    u^{1}_{i,j}=\Delta t\Psi(x_{i},y_{j})+(r_{1}(u^{0}_{i-1,j}+u^{0}_{i+1,j})+r_{2}(u^{0}_{i,j-1}+u^{0}_{i,j+1})+f(x_{i},y_{j},t_{0})\Delta t^{2})/2+(1-r_{1}-r_{2})u^{0}_{i,j} \space\space\space\space(4)

            由公式（4）知，公式（3）即为三层显格式：

    \left\{\begin{matrix} u^{k+1}_{i,j}=r_{1}(u^{k}_{i-1,j}+u^{k}_{i+1,j})+r_{2}(u^{0}_{i,j-1}+u^{k}_{i,j+1})+2(1-r_{1}-r_{2})u^{k}_{i,j}-u^{k-1}_{i,j}=f(x_{i},y_{j},t_{k})\Delta t^{2},1\leqslant i\leqslant m-1,1\leqslant j\leqslant n-1,1\leqslant k\leqslant l-1,\\ u^{0}_{i,j}=\varphi(x_{i},y_{j}),0\leqslant i\leqslant m,0\leqslant j\leqslant n,\\ u^{1}_{i,j}=\Delta t\Psi(x_{i},y_{j})+(r_{1}(u^{0}_{i-1,j}+u^{0}_{i+1,j})+r_{2}(u^{0}_{i,j-1}+u^{0}_{i,j+1})+f(x_{i},y_{j},t_{0})\Delta t^{2})/2+(1-r_{1}-r_{2})u^{0}_{i,j},1\leqslant i\leqslant m-1,1\leqslant j\leqslant n-1,\\ u^{k}_{0,j}=g_{1}(y_{j},t_{k}),u^{k}_{m,j}=g_{2}(y_{j},t_{k}),0\leqslant j\leqslant n,0<k\leqslant l,\\ u^{k}_{i,0}=g_{3}(x_{i},t_{k}),u^{k}_{i,n}=g_{4}(x_{i},t_{k}),0\leqslant i\leqslant m,0<k\leqslant l \end{matrix}\right.

    该格式的局部截断误差为O(\Delta t^{2}+\Delta x^{2}+\Delta y^{2})，考虑到其稳定性限制，将其改为隐格式。

    2.2 交替方向隐格式

            由于

    \frac{\partial ^{2}u}{\partial x^{2}}|_{(x_{i,}y_{j},t_{k})}\approx\frac{1}{2}(\frac{\partial ^{2}u}{\partial x^{2}}|_{(x_{i},y_{j},t_{k-1})}+\frac{\partial^{2}u}{\partial x^{2}}|_{(x_{i},y_{j},t_{k+1})})

    \frac{\partial ^{2}u}{\partial y^{2}}|_{(x_{i,}y_{j},t_{k})}\approx\frac{1}{2}(\frac{\partial ^{2}u}{\partial y^{2}}|_{(x_{i},y_{j},t_{k-1})}+\frac{\partial^{2}u}{\partial y^{2}}|_{(x_{i},y_{j},t_{k+1})})

    由上面两式可将原来在点(x_{i},y_{j},t_{k})处的连续方程

    \frac{\partial^{2}u}{\partial t^{2}}|_{(x_{i},y_{j},t_{k})}-(\frac{\partial^{2}u}{\partial x^{2}}+\frac{\partial^{2}u}{\partial y^{2}})|_{(x_{i},y_{j},t_{k})}=f(x_{i},y_{j},t_{k})

    改写为

    \frac{\partial^{2}u}{\partial t^{2}}|_{(x_{i},y_{j},t_{k})}-\frac{1}{2}((\frac{\partial^{2}u}{\partial x^{2}}+\frac{\partial^{2}u}{\partial y^{2}})|_{(x_{i},y_{j},t_{k-1})}+(\frac{\partial^{2}u}{\partial x^{2}}+\frac{\partial^{2}u}{\partial y^{2}})|_{(x_{i},y_{j},t_{k+1})})=f(x_{i},y_{j},t_{k})+O(\Delta t^{2})

            再用中心差商处理二阶偏导数，将数值解代替精确解并忽略高阶项，可得数值隐格式为：

    \frac{u^{k-1}_{i,j}-2u^{k}_{i,j}+u^{k+1}_{i,j}}{\Delta t^{2}}-\frac{1}{2}(\frac{u^{k-1}_{i-1,j}-2u^{k-1}_{i,j}+u^{k-1}_{i+1,j}}{\Delta x^{2}}+\frac{u^{k+1}_{i-1,j}-2u^{k+1}_{i,j}+u^{k+1}_{i+1,j}}{\Delta x^{2}})-\frac{1}{2}(\frac{u^{k-1}_{i,j-1}-2u^{k-1}_{i,j}+u^{k-1}_{i,j+1}}{\Delta y^{2}}+\frac{u^{k+1}_{i,j-1}-2u^{k+1}_{i,j}+u^{k+1}_{i,j+1}}{\Delta y^{2}})=f(x_{i},y_{j},t_{k}) \space\space(5)

            公式（5）在求解上存在困难，故参照二维抛物型偏微分方程初边值问题的交替方向隐格式设计思想，先将公式（5）写成算子的形式，可改写为：

    \frac{u^{k-1}_{i,j}-2u^{k}_{i,j}+u^{k+1}_{i,j}}{\Delta t^{2}}-\frac{1}{2}(\frac{\delta^{2}_{x}u^{k-1}_{i,j}}{\Delta x^{2}}+\frac{\delta^{2}_{x}u^{k+1}_{i,j}}{\Delta x^{2}})-\frac{1}{2}(\frac{\delta^{2}_{y}u^{k-1}_{i,j}}{\Delta y^{2}}+\frac{\delta^{2}_{y}u^{k+1}_{i,j}}{\Delta y^{2}})=f(x_{i},y_{j},t_{k})

    也就是          u^{k+1}_{i,j}-2^{k}_{i,j}+u^{k+1}_{i,j}=\frac{r_{1}}{2}(\delta^{2}_{x}u^{k-1}_{i,j}+\delta^{2}_{x}u^{k+1}_{i,j})+\frac{r_{2}}{2}(\delta^{2}_{y}u^{k-1}_{i,j}+\delta^{2}_{y}u^{k+1}_{i,j})+f(x_{i},y_{j},t_{k})\Delta t^{2}

    即

    (1-\frac{r_{1}}{2}\delta^{2}_{x}-\frac{r_{2}}{2}\delta^{2}_{y})u^{k+1}_{i,j}=(\frac{r_{1}}{2}\delta^{2}_{x}+\frac{r_{2}}{2}\delta^{2}_{y}-1)u^{k-1}_{i,j}+2u^{k}_{i,j}+f(x_{i},y_{j},t_{k})\Delta t^{2}

            对上式左端添加一个辅助项，即

    (1-\frac{r_{1}}{2}\delta^{2}_{x}-\frac{r_{2}}{2}\delta^{2}_{y}+\frac{r_{1}r_{2}}{4}\delta^{2}_{x}\delta^{2}_{y})u^{k+1}_{i,j}=(\frac{r_{1}}{2}\delta^{2}_{x}+\frac{r_{2}}{2}\delta^{2}_{y}-1)u^{k-1}_{i,j}+2u^{k}_{i,j}+f(x_{i},y_{j},t_{k})\Delta t^{2} \space\space(6)

            对公式（6）进行分解，可以写为

    (1-\frac{r_{1}}{2}\delta^{2}_{x})(1-\frac{r_{2}}{2}\delta^{2}_{y})u^{k+1}_{i,j}=(\frac{r_{1}}{2}\delta^{2}_{x}+\frac{r_{2}}{2}\delta^{2}_{y}-1)u^{k-1}_{i,j}+2u^{k}_{i,j}+f(x_{i},y_{j},t_{k})\Delta t^{2} \space\space(6)

            通过引入中间变量V_{i,j}，得

    \left\{\begin{matrix} (1-\frac{r_{1}}{2}\delta^{2}_{x})V_{i,j}=(\frac{r_{1}}{2}\delta^{2}_{x}+\frac{r_{2}}{2}\delta^{2}_{y}-1)u^{k-1}_{i,j}+2u^{k}_{i,j}+f(x_{i},y_{j},t_{k})\\ (1-\frac{r_{2}}{2}\delta^{2}_{y})u^{k+1}_{i,j}=V_{i,j} \space\space(7)\end{matrix}\right.

            上式是一个x方向的三对角线性方程组，计算第1式中的V_{i,j}时需要用到V_{0,j}和V_{m,j}，这可以直接从第2式中解得，即

    V_{0,j}=(1-\frac{r_{2}}{2}\delta^{2}_{y})u^{k+1}_{0,j},V_{m,j}=(1-\frac{r_{2}}{2}\delta^{2}_{y})u^{k+1}_{m,j} \space\space(8)

            我们可以直接将公式（7）、（8）写成差分形式，即

    \left\{\begin{matrix} -\frac{r_{1}}{2}V_{i-1,j}+(1+r_{1})V_{i,j}-\frac{r_{1}}{2}V_{i+1,j}=2u^{k}_{i,j}+f(x_{i},y_{j},t_{k})\Delta t^{2}+\\\frac{r_{1}}{2}(u^{k-1}_{i-1,j}+u^{k-1}_{i+1,j})+\frac{r_{2}}{2}(u^{k-1}_{i,j-1}+u^{k-1}_{i,j+1})-(1+r_{1}+r_{2})u^{k-1}_{i,j}\\ -\frac{r_{2}}{2}u^{k+1}_{i,j-1}+(1+r_{2})u^{k+1}_{i,j}-\frac{r_{2}}{2}u^{k+1}_{i,j+1}=V_{i,j} \space\space(9)\end{matrix}\right.

    其中，                            V_{0,j}=-\frac{r_{2}}{2}(u^{k+1}_{0,j-1}+u^{k+1}_{0,j+1})+(1+r_{2})u^{k+1}_{0,j}

    V_{m,j}=-\frac{r_{2}}{2}(u^{k+1}_{m,j-1}+u^{k+1}_{m,j+1})+(1+r_{2})u^{k+1}_{m,j}

            假设第k和k-1个时间层的信息已知，这样在公式（9）的第1式中，先固定某个j，这时公式（9）的第1式就是一个m-1阶线性方程组，其系数矩阵是三对角矩阵，可以用追赶法求解。每解一个方程组就可以得到一个在[0,a]x[0,b]矩形区域内行网格点（即行节点(x_{i},y_{j})）上的中间量V的信息，所以要得到矩形区域内所有的网格点信息，需要求解n-1个这样的线性系统。同样，公式（9）的第2式是一个y方向的三对角线性方程组时，求解时要先固定某个i，这时公式（9）的第2式是一个n-1阶线性方程组，系数矩阵是三对角矩阵，可以用追赶法求解，每解一个方程组得到第k+1个时间层上[0,a]x[0,b]矩形区域内列网格点（即(x_{i},y_{j},t_{k+1})）上的数值解的信息，所以要得到第k+1时间层上所有网格点的信息，需要求解m-1个这样的线性系统。这样就实现了x方向和y方向交替求解的隐格式。

    三、算例实现

            用交替方向隐格式求解下列二维双曲型方程初边值问题：

    \left\{\begin{matrix} \frac{\partial^{2}u}{\partial t^{2}}-(\frac{\partial^{2}u}{\partial x^{2}}+\frac{\partial^{2}u}{\partial y^{2}})=\frac{4t}{(1+x^{2}+y^{2})^{2}}(1-\frac{2(x^{2}+y^{2})}{1+x^{2}+y^{2}}),0<x,y<1,0<t\leqslant 1,\\ u(x,y,0)=0,\frac{\partial u}{\partial t}(x,y,0)=\frac{1}{1+x^{2}+y^{2}},0\leqslant x,y\leqslant 1,\\ u(0,y,t)=\frac{t}{1+y^{2}},u(1,y,t)=\frac{t}{2+y^{2}},0\leqslant y\leqslant 1,0<t\leqslant 1,\\ u(x,0,t)=\frac{t}{1+x^{2}},u(x,1,t)=\frac{t}{2+x^{2}},0<x<1,0<t\leqslant 1. \end{matrix}\right.

    已知精确解为u(x,y,t)=\frac{t}{1+x^{2}+y^{2}}。分别取步长为\Delta x=1/10,\Delta y=1/20,\Delta t=1/40和\Delta x=1/20,\Delta y=1/40,\Delta t=1/80，给出在节点(0.2i,0.25j,1.00),i=1,2,3,4,j=1,2,3处的数值解和误差。

    代码如下：

    1. #include
    2. #include
    3. #include
    4.  
    5.  
    6. int main(int argc, char* argv[])
    7. {
    8.         int i, j, k, m, n, L, gap_i, gap_j;
    9.         double a, b, T, r1, r2, dx, dy, dt, *x, *y, *t, ***u, **v;
    10.         double *a1, *b1, *c1, *d1, *a2, *b2, *c2, *d2, *ans, temp;
    11.         double f(double x, double y, double t);
    12.         double phi(double x, double y);
    13.         double psi(double x, double y);
    14.         double g1(double y, double t);
    15.         double g2(double y, double t);
    16.         double g3(double x, double t);
    17.         double g4(double x, double t);
    18.         double *chase_algorithm(double *a, double *b, double *c, double *d, int n);
    19.         double exact(double x, double y, double t);
    20.  
    21.         a = 1.0;
    22.         b = 1.0;
    23.         T = 1.0;
    24.         m = 10;
    25.         n = 20;
    26.         L = 40;
    27.         dx = a / m;
    28.         dy = b / n;
    29.         dt = T / L;
    30.         temp = dt / dx;
    31.         r1 = temp*temp;
    32.         temp = dt / dy;
    33.         r2 = temp*temp;
    34.         printf("m=%d, n=%d, L=%d.\n", m, n, L);
    35.         printf("r1=%.4f,   r2=%.4f.\n", r1, r2);
    36.  
    37.         x = (double *)malloc(sizeof(double)*(m + 1));
    38.         for (i = 0; i <= m; i++)
    39.                x[i] = i*dx;
    40.  
    41.         y = (double *)malloc(sizeof(double)*(n + 1));
    42.         for (j = 0; j <= n; j++)
    43.                y[j] = j*dy;
    44.  
    45.         t = (double *)malloc(sizeof(double)*(L + 1));
    46.         for (k = 0; k <= L; k++)
    47.                t[k] = k*dt;
    48.  
    49.         u = (double ***)malloc(sizeof(double **)*((m + 1)*(n + 1)*(L + 1)));
    50.         v = (double **)malloc(sizeof(double *)*((m + 1)*(n + 1)));
    51.  
    52.         for (i = 0; i <= m; i++)
    53.         {
    54.                u[i] = (double **)malloc(sizeof(double *)*((n + 1)*(L + 1)));
    55.                v[i] = (double *)malloc(sizeof(double)*(n + 1));
    56.         }
    57.  
    58.         for (i = 0; i <= m; i++)
    59.         {
    60.                for (j = 0; j <= n; j++)
    61.                        u[i][j] = (double *)malloc(sizeof(double)*(L + 1));
    62.         }
    63.  
    64.         for (i = 0; i <= m; i++)
    65.         {
    66.                for (j = 0; j <= n; j++)
    67.                {
    68.                        u[i][j][0] = phi(x[i], y[j]);
    69.                }
    70.         }
    71.  
    72.         for (i = 1; i< m; i++)
    73.         {
    74.                for (j = 1; j < n; j++)
    75.                {
    76.                        u[i][j][1] = u[i][j][0] + dt*psi(x[i], y[j]) + (r1*(u[i - 1][j][0] - 2 * u[i][j][0] + u[i + 1][j][0]) + r2*(u[i][j - 1][0] - 2 * u[i][j][0] + u[i][j + 1][0]) + dt*dt*f(x[i], y[j], t[0])) / 2.0;
    77.                }
    78.         }
    79.  
    80.         for (k = 1; k <= L; k++)
    81.         {
    82.                for (j = 0; j <= n; j++)
    83.                {
    84.                        u[0][j][k] = g1(y[j], t[k]);
    85.                        u[m][j][k] = g2(y[j], t[k]);
    86.                }
    87.                for (i = 1; i <= m - 1; i++)
    88.                {
    89.                        u[i][0][k] = g3(x[i], t[k]);
    90.                        u[i][n][k] = g4(x[i], t[k]);
    91.                }
    92.         }
    93.  
    94.         a1 = (double *)malloc(sizeof(double)*(m - 1));
    95.         b1 = (double *)malloc(sizeof(double)*(m - 1));
    96.         c1 = (double *)malloc(sizeof(double)*(m - 1));
    97.         d1 = (double *)malloc(sizeof(double)*(m - 1));
    98.         for (i = 0; i< m - 1; i++)
    99.         {
    100.                 a1[i] = -r1 / 2.0;
    101.                 b1[i] = 1.0 + r1;
    102.                 c1[i] = a1[i];
    103.         }
    104.  
    105.         a2 = (double *)malloc(sizeof(double)*(n - 1));
    106.         b2 = (double *)malloc(sizeof(double)*(n - 1));
    107.         c2 = (double *)malloc(sizeof(double)*(n - 1));
    108.         d2 = (double *)malloc(sizeof(double)*(n - 1));
    109.         for (j = 0; j < n - 1; j++)
    110.         {
    111.                 a2[j] = -r2 / 2.0;
    112.                 b2[j] = 1.0 + r2;
    113.                 c2[j] = a2[j];
    114.         }
    115.  
    116.         for (k = 1; k < L; k++)
    117.         {
    118.                 for (j = 1; j <= n - 1; j++)
    119.                 {
    120.                         for (i = 1; i <= m - 1; i++)
    121.                         {
    122.                                 d1[i-1]=2 * u[i][j][k] + dt*dt*f(x[i], y[j], t[k])+r1*(u[i-1][j][k-1]+u[i+1][j][k-1])/2.0+r2*(u[i][j-1][k-1]+u[i][j+1][k-1])/2.0-(1+r1+r2)*u[i][j][k-1];
    123.                         }
    124.  
    125.                         v[0][j] = -r2*(u[0][j - 1][k + 1] + u[0][j + 1][k + 1]) / 2.0 + (1 + r2)*u[0][j][k + 1];
    126.                         d1[0] = d1[0] + r1*v[0][j] / 2.0;
    127.                         v[m][j] = -r2*(u[m][j - 1][k + 1] + u[m][j + 1][k + 1]) / 2.0 + (1 + r2)*u[m][j][k + 1];
    128.                         d1[m - 2] = d1[m - 2] + r1*v[m][j] / 2.0;
    129.                         ans = chase_algorithm(a1, b1, c1, d1, m - 1);
    130.  
    131.                         for (i = 1; i <= m - 1; i++)
    132.                                 v[i][j] = ans[i - 1];
    133.  
    134.                         free(ans);
    135.                 }
    136.  
    137.                 for (i = 1; i <= m - 1; i++)
    138.                 {
    139.                         for (j = 1; j <= n - 1; j++)
    140.                                 d2[j - 1] = v[i][j];
    141.                         d2[0] = d2[0] + r2*u[i][0][k + 1] / 2.0;
    142.                         d2[n - 2] = d2[n - 2] + r2*u[i][n][k + 1] / 2.0;
    143.                         ans = chase_algorithm(a2, b2, c2, d2, n - 1);
    144.  
    145.                         for (j = 1; j <= n - 1; j++)
    146.                                 u[i][j][k + 1] = ans[j - 1];
    147.                         free(ans);
    148.                 }
    149.         }
    150.  
    151.         k = L ;
    152.         gap_i = m / 5;
    153.         gap_j = n / 4;
    154.  
    155.         for (i = gap_i; i <= m - 1; i = i + gap_i)
    156.         {
    157.                 for (j = gap_j; j <= n - 1; j = j + gap_j)
    158.                 {
    159.                        temp = fabs(exact(x[i], y[j], t[k]) - u[i][j][k]);
    160.                        printf("(%.2f, %.2f, %.2f)   y=%f,  err=%.4e\n", x[i], y[j], t[k], u[i][j][k], temp);
    161.                 }
    162.         }
    163.  
    164.         free(x); free(y); free(t);
    165.         free(a1); free(b1); free(c1); free(d1);
    166.         free(a2); free(b2); free(c2); free(d2);
    167.         for (i = 0; i <= m; i++)
    168.         {
    169.                 for (j = 0; j <= n; j++)
    170.                         free(u[i][j]);
    171.         }
    172.         for (i = 0; i <= m; i++)
    173.         {
    174.                 free(u[i]);
    175.         }
    176.         free(u);
    177.  
    178.         return 0;
    179. }
    180.  
    181.  
    182.  
    183. double f(double x, double y, double t)
    184. {
    185.         double z,temp;
    186.  
    187.         z = x*x + y*y;
    188.         temp = 1 - 2 * z / (1 + z);
    189.  
    190.         return 4*t*temp/((1+z)*(1+z));
    191. }
    192. double phi(double x, double y)
    193. {
    194.         return 0.0;
    195. }
    196. double psi(double x, double y)
    197. {
    198.         return 1.0/(1+x*x+y*y);
    199. }
    200. double g1(double y, double t)
    201. {
    202.         return t/(1+y*y);
    203. }
    204. double g2(double y, double t)
    205. {
    206.         return t/(2+y*y);
    207. }
    208. double g3(double x, double t)
    209. {
    210.         return t/(1+x*x);
    211. }
    212. double g4(double x, double t)
    213. {
    214.         return t/(2+x*x);
    215. }
    216. double *chase_algorithm(double *a, double *b, double *c, double *d, int n)
    217. {
    218.         int i;
    219.         double * ans, *g, *w, p;
    220.  
    221.         ans = (double *)malloc(sizeof(double)*n);
    222.         g = (double *)malloc(sizeof(double)*n);
    223.         w = (double *)malloc(sizeof(double)*n);
    224.         g[0] = d[0] / b[0];
    225.         w[0] = c[0] / b[0];
    226.  
    227.         for (i = 1; i
    228.         {
    229.                 p = b[i] - a[i] * w[i - 1];
    230.                 g[i] = (d[i] - a[i] * g[i - 1]) / p;
    231.                 w[i] = c[i] / p;
    232.         }
    233.         ans[n - 1] = g[n - 1];
    234.         i = n - 2;
    235.         do
    236.         {
    237.                 ans[i] = g[i] - w[i] * ans[i + 1];
    238.                 i = i - 1;
    239.         } while (i >= 0);
    240.  
    241.         free(g);
    242.         free(w);
    243.  
    244.         return ans;
    245. }
    246. double exact(double x, double y, double t)
    247. {
    248.         return t/(1+x*x+y*y);
    249. }
    250.

    当\Delta x=1/10,\Delta y=1/20,\Delta t=1/40时，计算结果如下：

    1. m=10, n=20, L=40.
    2. r1=0.0625,   r2=0.2500.
    3. (0.20, 0.25, 1.00)   y=0.907133,  err=1.0342e-04
    4. (0.20, 0.50, 1.00)   y=0.775225,  err=3.0722e-05
    5. (0.20, 0.75, 1.00)   y=0.624030,  err=4.5462e-06
    6. (0.40, 0.25, 1.00)   y=0.817921,  err=7.4625e-05
    7. (0.40, 0.50, 1.00)   y=0.709103,  err=1.1636e-04
    8. (0.40, 0.75, 1.00)   y=0.580475,  err=7.6977e-05
    9. (0.60, 0.25, 1.00)   y=0.702808,  err=1.7953e-04
    10. (0.60, 0.50, 1.00)   y=0.620917,  err=2.0139e-04
    11. (0.60, 0.75, 1.00)   y=0.520023,  err=1.3270e-04
    12. (0.80, 0.25, 1.00)   y=0.587236,  err=1.3524e-04
    13. (0.80, 0.50, 1.00)   y=0.528946,  err=1.5470e-04
    14. (0.80, 0.75, 1.00)   y=0.453919,  err=1.1003e-04

    当\Delta x=1/20,\Delta y=1/40,\Delta t=1/80时，计算结果如下：

    1. m=20, n=40, L=80.
    2. r1=0.0625,   r2=0.2500.
    3. (0.20, 0.25, 1.00)   y=0.907056,  err=2.6327e-05
    4. (0.20, 0.50, 1.00)   y=0.775202,  err=7.7268e-06
    5. (0.20, 0.75, 1.00)   y=0.624026,  err=9.2774e-07
    6. (0.40, 0.25, 1.00)   y=0.817978,  err=1.8204e-05
    7. (0.40, 0.50, 1.00)   y=0.709191,  err=2.8662e-05
    8. (0.40, 0.75, 1.00)   y=0.580532,  err=1.9294e-05
    9. (0.60, 0.25, 1.00)   y=0.702943,  err=4.4834e-05
    10. (0.60, 0.50, 1.00)   y=0.621068,  err=5.0469e-05
    11. (0.60, 0.75, 1.00)   y=0.520123,  err=3.2859e-05
    12. (0.80, 0.25, 1.00)   y=0.587338,  err=3.3376e-05
    13. (0.80, 0.50, 1.00)   y=0.529063,  err=3.7709e-05
    14. (0.80, 0.75, 1.00)   y=0.454003,  err=2.6860e-05

    四、结论

            从计算结果可以看出，将时间、空间步长同时减小1/2，误差减小1/4，可见该数值格式是二阶的。

  • 相关阅读:
    kali Linux常用快捷键及vim的基本使用
    AI 边缘计算平台 - 爱芯元智 AX620A 爱芯派开箱
    《拼多多电商业务场景》批量采集产品数据根据关键词获取商品列表示例
    Self-attention与multi-head self-attention
    C++中地递增递减运算符和指针
    react 使用笔记
    compact unwind compressed function offset doesn‘t fit in 24 bits
    MYSQL：主从复制简述
    HTTP协议中的Cookie和Session
    Nginx中配置GZIP压缩详解
  • 原文地址：https://blog.csdn.net/L_peanut/article/details/138168002