小白也能看懂的 ROC 曲线详解

作者：PrimiHub-Kevin

ROC 曲线是一种坐标图式的分析工具，是由二战中的电子和雷达工程师发明的，发明之初是用来侦测敌军飞机、船舰，后来被应用于医学、生物学、犯罪心理学。

如今，ROC 曲线已经被广泛应用于机器学习领域的模型评估，说到这里就不得不提到 Tom Fawcett 大佬，他一直在致力于推广 ROC 在机器学习领域的应用，他发布的论文《An introduction to ROC analysis》更是被奉为 ROC 的经典之作（引用 2.2w 次），知名机器学习库 scikit-learn 中的 ROC 算法就是参考此论文实现，可见其影响力！

不知道大多数人是否和我一样，对于 ROC 曲线的理解只停留在调用 scikit-learn 库的函数，对于它的背后原理和公式所知甚少。

前几天我重读了《An introduction to ROC analysis》终于将 ROC 曲线彻底搞清楚了，独乐乐不如众乐乐！如果你也对 ROC 的算法及实现感兴趣，不妨花些时间看完全文，相信你一定会有所收获！

一、什么是 ROC 曲线

下图中的蓝色曲线就是 ROC 曲线，它常被用来评价二值分类器的优劣，即评估模型预测的准确度。

二值分类器，就是字面意思它会将数据分成两个类别(正/负样本)。例如：预测银行用户是否会违约、内容分为违规和不违规，以及广告过滤、图片分类等场景。篇幅关系这里不做多分类 ROC 的讲解。

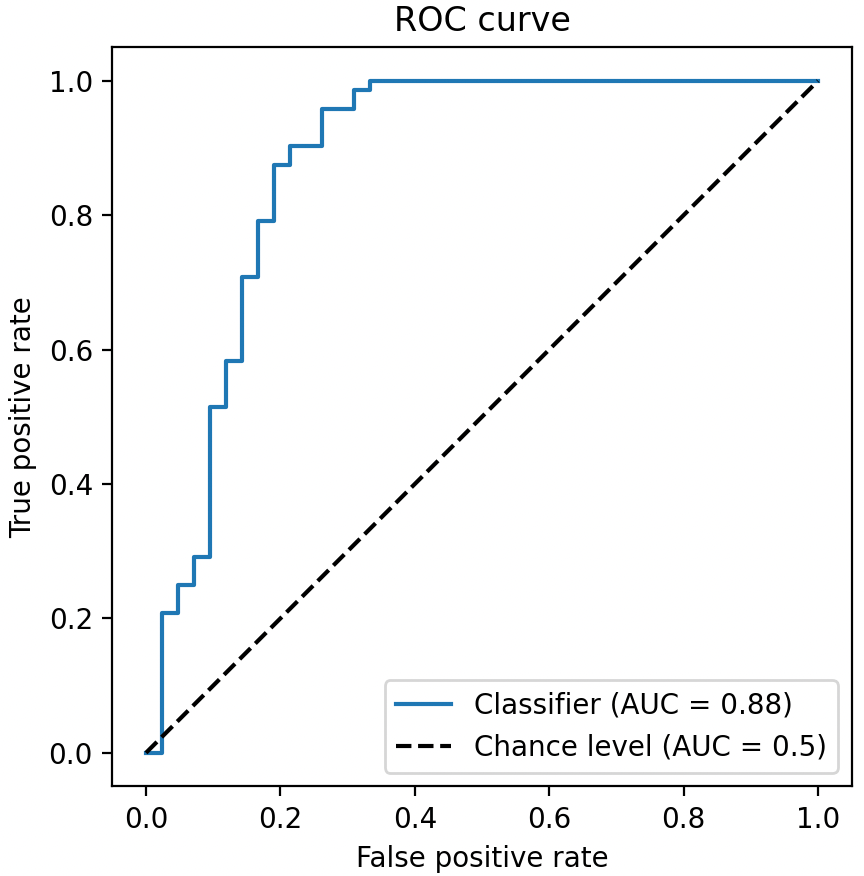
坐标系中纵轴为 TPR（真阳率/命中率/召回率）最大值为 1，横轴为 FPR（假阳率/误判率）最大值为 1，虚线为基准线（最低标准），蓝色的曲线就是 ROC 曲线。其中 ROC 曲线距离基准线越远，则说明该模型的预测效果越好。(TPR: True positive rate; FPR: False positive rate)

• ROC 曲线接近左上角：模型预测准确率很高
• ROC 曲线略高于基准线：模型预测准确率一般
• ROC 低于基准线：模型未达到最低标准，无法使用

二、背景知识

考虑一个二分类模型， 负样本(Negative) 为 0，正样本(Positive) 为 1。即：

• 标签 $y$ 的取值为 0 或 1。
• 模型预测的标签为 $\hat{y}$，取值也是 0 或 1。

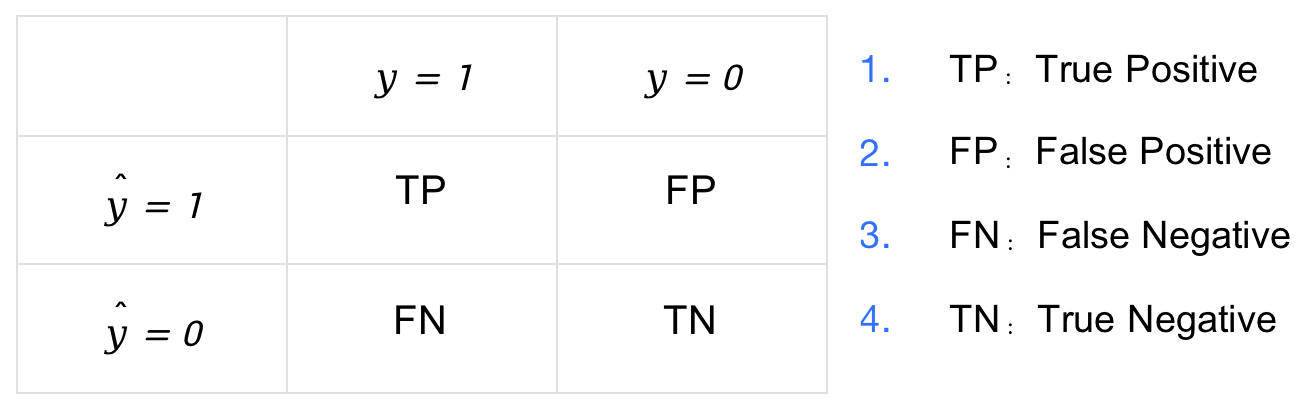
因此，将 $y$ 与 $\hat{y}$ 两两组合就会得到 4 种可能性，分别称为：

2.1 公式

ROC 曲线的横坐标为 FPR（False Positive Rate），纵坐标为 TPR（True Positive Rate）。FPR 统计了所有负样本中 预测错误(FP) 的比例，TPR 统计了所有正样本中 预测正确(TP) 的比例，其计算公式如下，其中 # 表示统计个数，例如 #N 表示负样本的个数，#P 表示正样本的个数

$\text{FPR}=\frac{\#\text{FP}}{\#\text{N}}$，$\text{TPR}=\frac{\#\text{TP}}{\#\text{P}}$

2.2 计算方法

下面举一个实际例子作为讲解，以下表 5 个样本为例，讲解如何计算 FPR 和 TPR。

正样本数 #P=3，负样本数 #N=2。

其中 $y=0$ 且 $\hat{y}=1$ 的样本有 1 个，即 #FP=1，所以 FPR=1/2=0.5

其中 $y=1$ 且 $\hat{y}=1$ 的样本有 2 个，即 #TP=2，所以 FPR=2/3

FPR 和 TPR 的取值范围均是 0 到 1 之间。对于 FPR，我们希望其越小越好。而对于 TPR，我们希望其越大越好。

至此，我们已经介绍完如何计算 FPR 和 TPR 的值，下面将会讲解如何绘制 ROC 曲线。

三、绘制 ROC 曲线

讲到这里，可能有的同学会问：ROC 不是一条曲线吗？讲了这么多它到底应该怎么画呢？下面将分为两部分讲解如何绘制 ROC 曲线，直接打通你的“任督二脉”彻底拿下 ROC 曲线：

• 第一部分：通过手绘的方式讲解原理
• 第二部分：Python 代码实现，代码清爽易读

如果说上面是“开胃小菜”，那下面就是正菜啦！

---

3.1 手绘 ROC 曲线

一般在二分类模型里（标签取值为 0 或 1），会默认设定一个阈值 (threshold)。当预测分数大于这个阈值时，输出 1，反之输出 0。我们可以通过调节这个阈值，改变模型预测的输出，进而画出 ROC 曲线。

以下面表格中的 20 个点为例，介绍如何人工画出 ROC 曲线，其中正样本和负样本都是 10 个，即 #P = #N = 10。

当设定阈值为 0.9 时，只有第一个点预测为 1，其余都为 0，故 #FP=0、#TP=1，计算出 FPR=0/10=0，TPR=1/10=0.1，画出点 (0，0.1)

当设定阈值为 0.8 时，只有前两个点预测为 1，其余都为 0，故 #FP=0、#TP=2，计算出 FPR=0/10=0，TPR=2/10=0.2，画出点 (0，0.2)

当设定阈值为 0.7 时，只有前三个点预测为 1，其余都为 0，故 #FP=1、#TP=2，计算出 FPR=1/10=0.1，TPR=2/10=0.2，画出点 (0.1，0.2)。

以此类推，画出的 ROC 曲线如下：

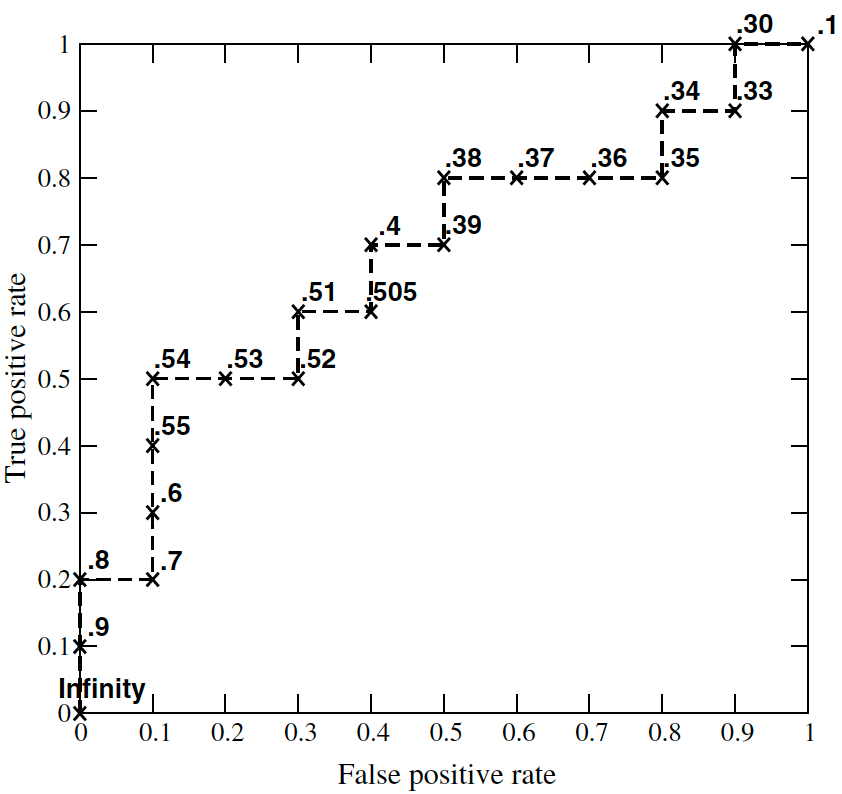
因此，在画 ROC 曲线前，需要将预测分数从大到小排序，然后将预测分数依次设定为阈值，分别计算 FPR 和 TPR。而对于基准线，假设随机预测为正样本的概率为 $x$，即 $\mathrm{Pr}(\hat{y}=1)=x$ 由于 FPR 计算的是负样本中，预测为正样本的概率，因此 FPR=$x$（同理，TPR=$x$）。所以，基准线为从点 (0, 0) 到 (1, 1) 的斜线。

3.2 Python 代码

接下来，我们将结合代码讲解如何在 Python 中绘制 ROC 曲线。

下面的代码参考了《An Introduction to ROC Analysis》中的算法 1（伪代码）。值得一提的是，知名机器学习库 scikit-learn 的 roc_curve 函数 也参考了这个算法。

下面我自己实现的 roc 函数可以理解为是简化版的 roc_curve，这里的代码逻辑更加简洁易懂，算法的时间复杂度 $O(n\log n)$。完整的代码如下：

# import numpy as np
def roc(y_true, y_score, pos_label):
    """
    y_true：真实标签
    y_score：模型预测分数
    pos_label：正样本标签，如“1”
    """
    # 统计正样本和负样本的个数
    num_positive_examples = (y_true == pos_label).sum()
    num_negtive_examples = len(y_true) - num_positive_examples

    tp, fp = 0, 0
    tpr, fpr, thresholds = [], [], []
    score = max(y_score) + 1
    
    # 根据排序后的预测分数分别计算fpr和tpr
    for i in np.flip(np.argsort(y_score)):
        # 处理样本预测分数相同的情况
        if y_score[i] != score:
            fpr.append(fp / num_negtive_examples)
            tpr.append(tp / num_positive_examples)
            thresholds.append(score)
            score = y_score[i]
            
        if y_true[i] == pos_label:
            tp += 1
        else:
            fp += 1

    fpr.append(fp / num_negtive_examples)
    tpr.append(tp / num_positive_examples)
    thresholds.append(score)

    return fpr, tpr, thresholds
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

导入上面 3.1 表格中的数据，通过上面实现的 roc 方法，计算 ROC 曲线的坐标值。

import numpy as np

y_true = np.array(
    [1, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0]
)
y_score = np.array([
    .9, .8, .7, .6, .55, .54, .53, .52, .51, .505,
    .4, .39, .38, .37, .36, .35, .34, .33, .3, .1
])

fpr, tpr, thresholds = roc(y_true, y_score, pos_label=1)
1
2
3
4
5
6
7
8
9
10
11

最后，通过 Matplotlib 将计算出的 ROC 曲线坐标绘制成图。

import matplotlib.pyplot as plt

plt.plot(fpr, tpr)
plt.axis("square")
plt.xlabel("False positive rate")
plt.ylabel("True positive rate")
plt.title("ROC curve")
plt.show()
1
2
3
4
5
6
7
8

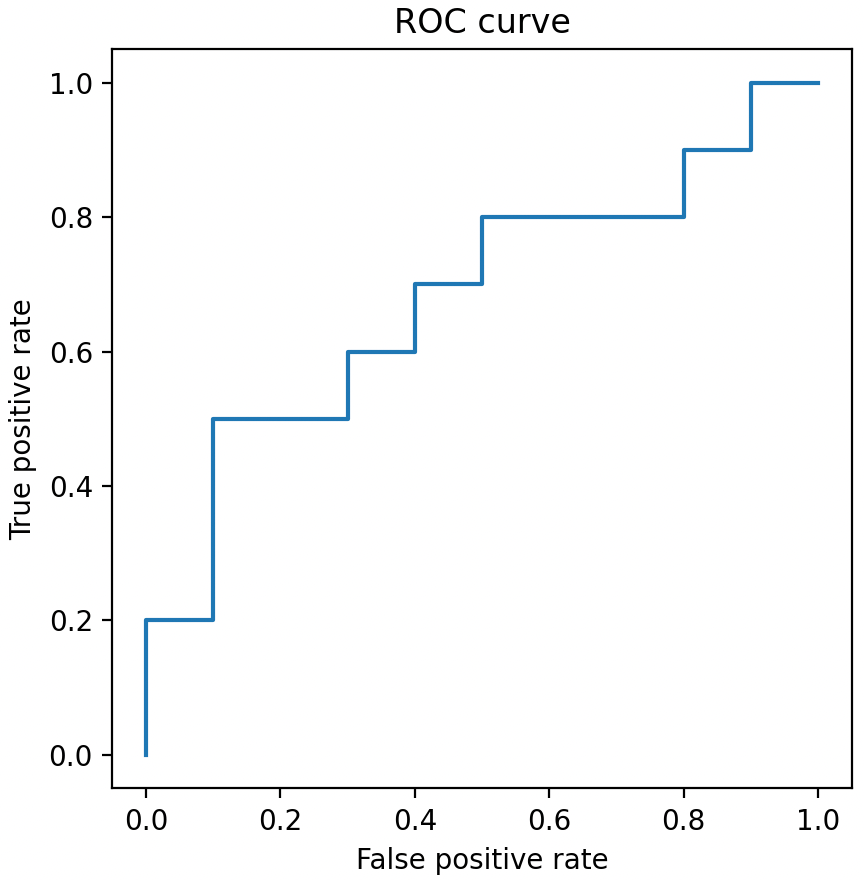
至此，ROC 的基础知识部分就全部讲完了，如果还想深入了解的同学可以继续往下看。

四、联邦学习中的 ROC 平均

如果将上面的内容比作“正餐”，那这里就是妥妥干货了，打起精神冲鸭！

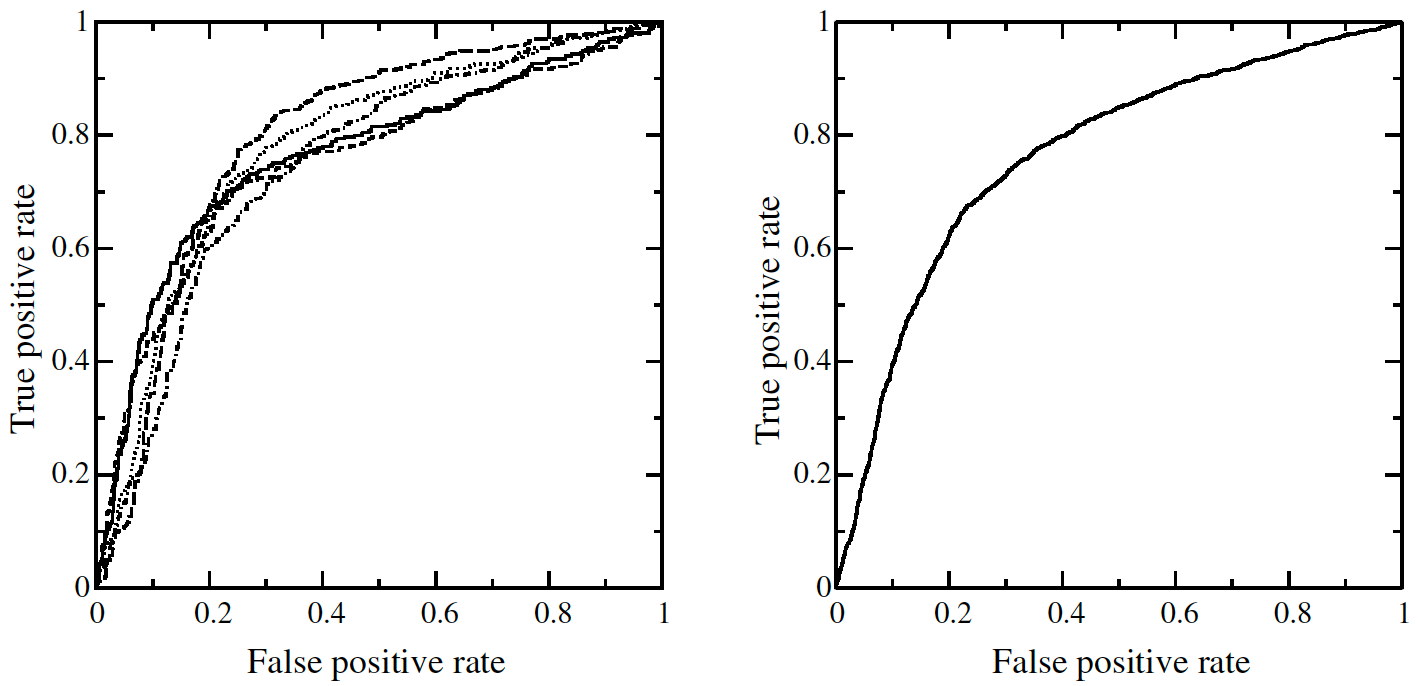
顾名思义，ROC 平均就是将多条 ROC 曲线“平均化”。那么，什么场景需要做 ROC 平均呢？例如：横向联邦学习中，由于样本都在用户本地，服务器可以采用 ROC 平均的方式，计算近似的全局 ROC 曲线。

ROC 的平均有两种方法：垂直平均、阈值平均，下面将逐一进行讲解，并给出 Python 代码实现。

4.1 垂直平均

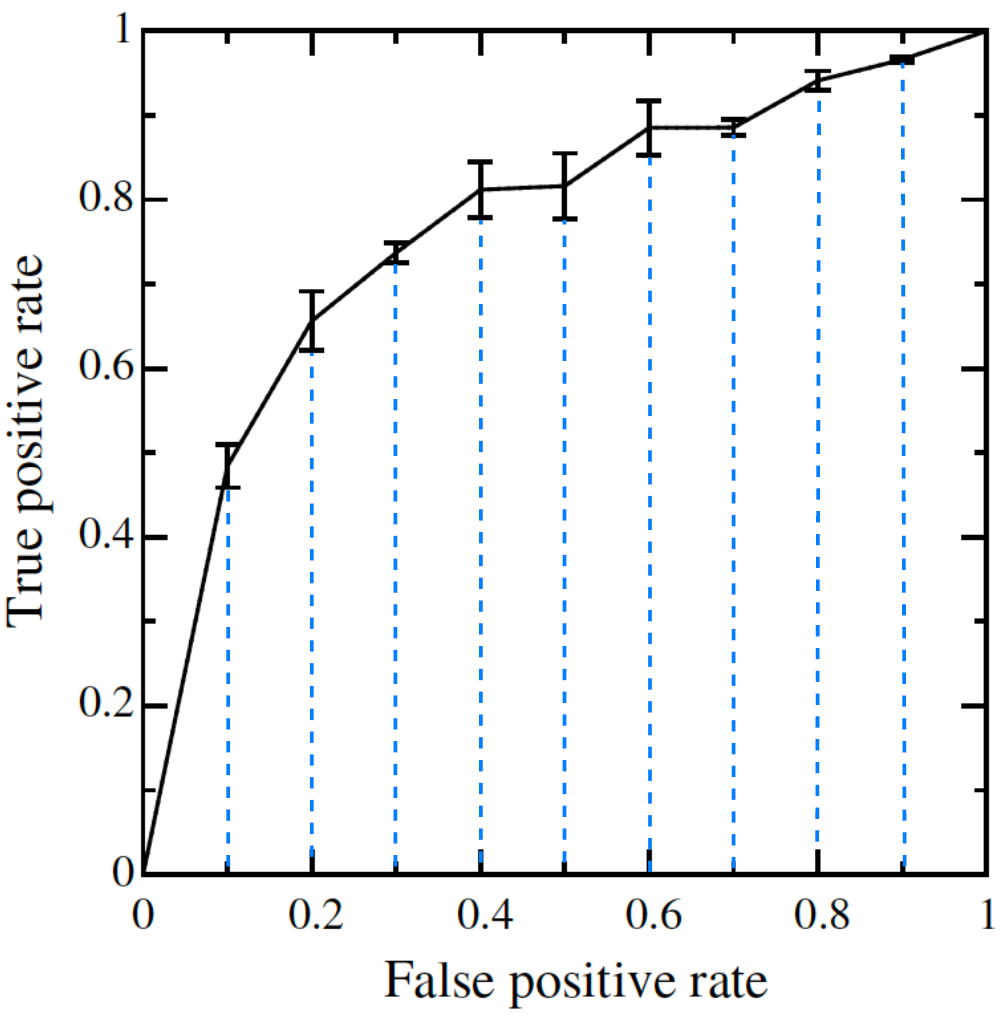
垂直平均（Vertical averaging）的思想是，选取一些 FPR 的点，计算其平均的 TPR 值。下面是论文中的算法描述的伪代码，看不懂可直接略过看 Python 代码实现部分。

下面是 Python 的代码实现：

# import numpy as np
def roc_vertical_avg(samples, FPR, TPR):
    """
    samples：选取FPR点的个数
    FPR：包含所有FPR的列表
    TPR：包含所有TPR的列表
    """
    nrocs = len(FPR)
    tpravg = []
    fpr = [i / samples for i in range(samples + 1)]

    for fpr_sample in fpr:
        tprsum = 0
        # 将所有计算的tpr累加
        for i in range(nrocs):
            tprsum += tpr_for_fpr(fpr_sample, FPR[i], TPR[i])
        # 计算平均的tpr
        tpravg.append(tprsum / nrocs)

    return fpr, tpravg

# 计算对应fpr的tpr
def tpr_for_fpr(fpr_sample, fpr, tpr):
    i = 0
    while i < len(fpr) - 1 and fpr[i + 1] <= fpr_sample:
        i += 1

    if fpr[i] == fpr_sample:
        return tpr[i]
    else:
        return interpolate(fpr[i], tpr[i], fpr[i + 1], tpr[i + 1], fpr_sample)

# 插值
def interpolate(fprp1, tprp1, fprp2, tprp2, x):
    slope = (tprp2 - tprp1) / (fprp2 - fprp1)
    return tprp1 + slope * (x - fprp1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

4.2 阈值平均

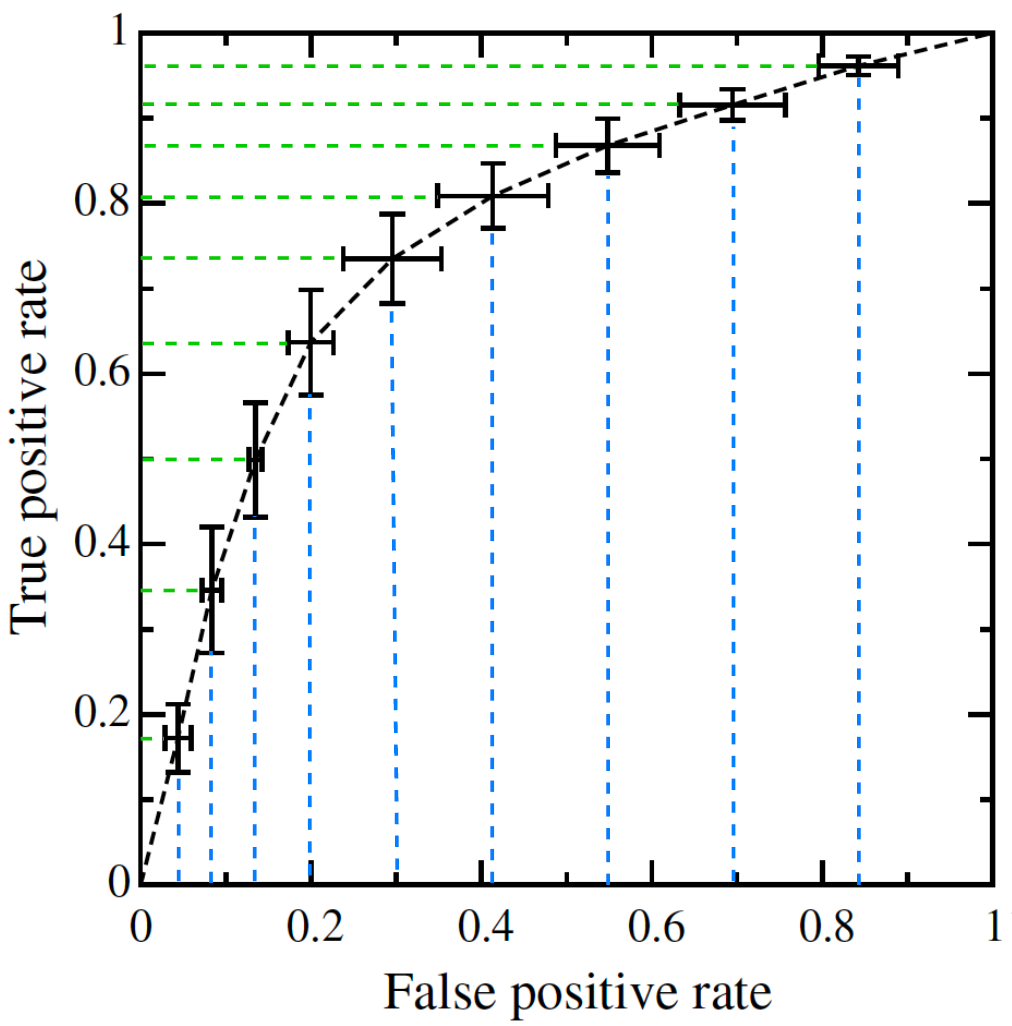
阈值平均（Threshold averaging）的思想是，选取一些阈值的点，计算其平均的 FPR 和 TPR。

下面是 Python 的代码实现：

# import numpy as np
def roc_threshold_avg(samples, FPR, TPR, THRESHOLDS):
    """
    samples：选取FPR点的个数
    FPR：包含所有FPR的列表
    TPR：包含所有TPR的列表
    THRESHOLDS：包含所有THRESHOLDS的列表
    """
    nrocs = len(FPR)
    T = []
    fpravg = []
    tpravg = []

    for thresholds in THRESHOLDS:
        for t in thresholds:
            T.append(t)
    T.sort(reverse=True)

    for tidx in range(0, len(T), int(len(T) / samples)):
        fprsum = 0
        tprsum = 0
        # 将所有计算的fpr和tpr累加
        for i in range(nrocs):
            fprp, tprp = roc_point_at_threshold(FPR[i], TPR[i], THRESHOLDS[i], T[tidx])
            fprsum += fprp
            tprsum += tprp
        # 计算平均的fpr和tpr
        fpravg.append(fprsum / nrocs)
        tpravg.append(tprsum / nrocs)

    return fpravg, tpravg

# 计算对应threshold的fpr和tpr
def roc_point_at_threshold(fpr, tpr, thresholds, thresh):
    i = 0
    while i < len(fpr) - 1 and thresholds[i] > thresh:
        i += 1
    return fpr[i], tpr[i]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

在我们的 PrimiHub 联邦学习模块中，就实现了上述 ROC 平均方法。

五、最后

本文由浅入深地详细介绍了 ROC 曲线算法，包含算法原理、公式、计算、源码实现和讲解，希望能够帮助读者一口气（看的时候可得喘气 😮‍💨）搞懂 ROC。

虽然 ROC 是个不起眼的知识点，但能网上能彻底讲清楚 ROC 的文章并不多。所以我又花时间重温了一遍 Tom Fawcett 的经典论文《An introduction to ROC analysis》，并将论文的内容抽丝剥茧、配上通俗易懂的 Python 代码，最终写出了这篇文章。再次致敬🫡 Tom Fawcett，感谢他在机器学习领域的贡献！

---

我们是 PrimiHub 密码学专家团队，用心去写每一篇内容，让每一位点开文章的读者都能有所收获。我们的内容专注于隐私计算领域，偶尔也涉及下机器学习领域。如果大家喜欢这个系列请留言告诉我们，它的姐妹篇 ACU 详解直接安排！

PrimiHub 一款由密码学专家团队打造的开源隐私计算平台，专注于分享数据安全、密码学、联邦学习、同态加密等隐私计算领域的技术和内容。