使用R语言计算并绘制流体力学中的二维泊肃叶流

平行平板间的二维流动

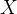  在流体力学中，当考虑两平行平板间的二维、定常、不可压缩流动，并且只存在沿x方向的流动速度，我们可以从N-S方程推导出方向的动量方程。对于给定的方程： 

       (式1)

  其中，是压力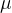，是动力粘度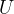，是x方向的速度分量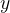，是与平板垂直的方向。

如果我们假设将压力梯度 看作一个常数 （负号是为了方便，因为通常压力在流动方向上是减小的），然后对方程进行积分：

积分一次得到：

,

 

再积分一次得到：

,

其中，和 是积分常数，可以通过边界条件来确定。

在R语言中，我们可以定义这个函数，并给定边界条件来求解 和。例如，假设在 时，，在 时，（即两平板间的距离为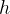，且在平板上速度为零），那么我们可以得到：

所以最终的解为：

.

library(ggplot2)  
 
G <- 1.0  # 压力梯度
mu <- 1.0  # 动力粘度  
h <- -1.0  # 平板间距  
  
# 设置y值范围  
y <- seq(0, h, length.out = 100)  
  
# 计算速度分布  
u <- function(y, G, mu, h) {  
  return((G / (2 * mu)) * (h * y - y^2))  
}  
  
# 计算速度  
u_values <- u(y, G, mu, h)  
  
# 存储y和u的值  
df <- data.frame(y = y, u = u_values)  
  
ggplot(df, aes(x = y, y = u)) +  
  geom_line() +                  
  labs(x = "y", y = "u(y)") +   
  ggtitle("速度分布图") +        
  theme_minimal()                

 

二维泊肃叶流 

  假设上下两个平板不动，则边界条件为无滑移条件：对式(1)积分两次，由边界条件得

        (式2)

式中 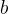是平板间距的一半（因为平板位于 和）

library(ggplot2)  
  
b <- 1.0 # 平板间距的一半  
mu <- 1.0 # 动力粘度  
dp_dx <- -1.0 # 压力梯度 
  
# 创建y值的细粒度向量  
y <- seq(-b, b, length.out = 100)  
  
# 速度分布函数  
u <- function(y, b, mu, dp_dx) {  
  return(-(1/(2*mu)) * dp_dx * (b^2 - y^2))  
}  
  
# 计算速度分布  
u_values <- u(y, b, mu, dp_dx)  
  
df <- data.frame(y = y, u = u_values)  
  
ggplot(df, aes(x = y, y = u)) +  
  geom_line(color = "black", linewidth = 1.0) + 
  geom_point(data = data.frame(y = c(-b, b), u = 0), aes(x = y, y = u),color = "red", size = 1, shape = 19) +  
labs(x = "y", y = "u(y)", title = "二维泊肃叶流速度分布图") + 
  theme_minimal() 

 

该式为流场中的速度分布，由式(2)可以分别计算出中线上最大速度值: 

  

library(ggplot2) 
 
mu <- 1.0     # 动力粘度 
dp_dx <- -0.1   # 压力梯度
b <- 1.0       # 流道的一半宽度
 
# 最大速度  
u_max <- -1 / (2 * mu) * dp_dx * b^2  
cat("中线上的最大速度 u_max 为：", u_max, "m/s\n")  
 
b_values <- seq(0.01, 0.1, by = 0.01)  # 流道宽度范围  
dp_dx_values <- seq(-50, -200, by = -50)  # 压力梯度范围  
mu_fixed <- mu  # 固定动力粘度  
 
u_max_matrix <- matrix(0, nrow = length(b_values), ncol = length(dp_dx_values))  
 
for (i in 1:length(b_values)) {  
  for (j in 1:length(dp_dx_values)) {  
    u_max_matrix[i, j] <- -1 / (2 * mu_fixed) * dp_dx_values[j] * b_values[i]^2  
  }  
}  
 
# 绘制- u_max作为b和dp/dx的函数  
df <- expand.grid(b = b_values, dp_dx = dp_dx_values)  
df$u_max <- as.vector(t(u_max_matrix))  
ggplot(df, aes(x = b, y = u_max, color = factor(dp_dx))) +  
  geom_line() +  
  labs(x = "流道半宽(b)",  
       y = "最大速度(u_max)",  
       color = "压力梯度(dp/dx)") +  
  scale_color_discrete(breaks = rev(dp_dx_values), labels = paste0("dp/dx = ", 
                                rev(dp_dx_values), " Pa/m")) +  
  theme_minimal()

 

通过两板间的流量 :

library(ggplot2) 
 
mu <- 1.0  # 动力粘度, 单位 Pa·s  
 
b_values <- seq(0.01, 0.1, by = 0.01)  # 流道宽度范围  
dp_dx_values <- seq(-50, -500, by = -50)  # 压力梯度范围  
mu_fixed <- mu  # 固定动力粘度  
 
# 初始化一个矩阵来存储结果  
Q_matrix <- matrix(0, nrow = length(b_values), ncol = length(dp_dx_values))  
 
# 计算不同参数下的流量Q  
for (i in 1:length(b_values)) {  
  for (j in 1:length(dp_dx_values)) {  
    Q_matrix[i, j] <- -(b_values[i]^3) / (3 * mu_fixed) * dp_dx_values[j]  
  }  
}  
 
df <- as.data.frame(as.table(Q_matrix))  
names(df) <- c("b", "dp_dx", "Q")  
df$b <- rep(b_values, each = length(dp_dx_values))  
df$dp_dx <- rep(dp_dx_values, times = length(b_values))  
 
# 绘制-Q为b和dp/dx的函数  
ggplot(df, aes(x = b, y = Q, color = factor(dp_dx))) +  
  geom_line() +  
  labs(x = "流道半宽(b)",  
       y = "流量(Q)",  
       color = "压力梯度(dp/dx)") +  
  scale_color_discrete(breaks = rev(unique(df$dp_dx)), 
                       labels = paste0("dp/dx = ", rev(unique(df$dp_dx)), " Pa/m")) +  
  theme_minimal()

 

两平板间流动的平均速度:

library(ggplot2)  
  
u <- function(y, b, mu, dp_dx) {  
  return(-(1/(2*mu)) * dp_dx * (b^2 - y^2))  
}  
  
b <- 1.0  # 平板间距的一半  
mu <- 1.0  # 动力粘度  
dp_dx <- -1.0  # 压力梯度  
  
# 最大速度 u_max  
u_max <- u(0, b, mu, dp_dx)  
  
# 计算平均速度 u_avg  
u_avg <- (2/3) * u_max  
  
# 创建向量来计算速度分布  
y_values <- seq(-b, b, length.out = 100)  
u_values <- sapply(y_values, u, b=b, mu=mu, dp_dx=dp_dx)  
df <- data.frame(y = y_values, u = u_values)  
  
ggplot(df, aes(x = y, y = u)) +  
  geom_line(color = "black", size = 0.8) +  
  geom_hline(yintercept = u_avg, color = "red", linetype = "dashed") + labs(x = "y", y = "u(y)", title = "二维泊肃叶流平均流速分布图") + 
  theme_minimal() +annotate("text", x = 0, 
y = u_avg + 0.05, label = paste("平均流速 =", round(u_avg, 2)))

 

壁面上的最大切应力： 

library(ggplot2)  
  
mu <- 1.0  
u_avg_base <- 0.33   
dp_dx_values <- c(-0.5, -1.0, -1.5)  
  
all_data <- data.frame()  
  
for (dp_dx in dp_dx_values) {  
  b_values <- seq(0.1, 1.0, by = 0.1)  # 
  tau_max_values <- sapply(b_values, function(b) {  
    return(dp_dx * b)  # 
  })  
 
  df <- data.frame(b = b_values, tau_max = tau_max_values, dp_dx = dp_dx)  
  all_data <- rbind(all_data, df)  
}  
  
 
ggplot(all_data, aes(x = b, y = tau_max, color = factor(dp_dx))) +  
  geom_line(size = 0.8) +  
  scale_color_discrete(name = "压力梯度 (dp/dx)", labels = paste("dp/dx =", dp_dx_values)) +  
  labs(x = "b (平板间距的一半)", y = "τ_max (壁面最大切应力)", title = "二维泊肃叶流壁面最大切应力") +  
  theme_minimal()

 

阻力系数： 

library(ggplot2)  
  
rho <- 1000  # 流体密度 (kg/m3)  
u_avg <-100  # 平均速度 (m/s)  
dp_dx_values <- seq(-100, 0, by = 10)  # 压力梯度范围 (Pa/m)
h_values <- seq(0.01, 0.1, by = 0.01)  # 平板间距范围 (m)  
  
lambda_data <- data.frame()  
  
for (dp_dx in dp_dx_values) {  
  for (h in h_values) {  
    tau_max <- -dp_dx * h / 2   
    lambda <- abs(tau_max) / (0.5 * rho * u_avg^2)  
    lambda_data <- rbind(lambda_data, data.frame(dp_dx = dp_dx, h = h, lambda = lambda))  
  }  
}  
  
ggplot(lambda_data, aes(x = h, y = lambda, color = factor(dp_dx))) +  
  geom_line(size = 1) +  
  scale_color_discrete(name = "压力梯度 (dp/dx)", breaks = dp_dx_values, labels = paste("dp/dx =", dp_dx_values)) +  
  labs(x = "平板间距 (h)", y = "阻力系数 (λ)", title = "二维泊肃叶流阻力系数曲线") +  
  theme_minimal()