K近邻模型

k近邻模型

基本思想

$k$近邻算法还是很直观的，准确的来说它不是一种学习算法，而是一种统计方法，不具备学习过程，一次性就可以给出结果。
其本质思想是将特征空间划分成一个个的单元($cell$)，其中每个$cell$的区域由距离该点比其他点更近的所有点定义，所有的$cell$组成了整特征空间。

如上图所示：
考虑样本$x_1$构成的$cell$，记作$cel{l}_{x_1}$

• 对于$x_2$，其距离$x_3$比$x_1$近，因此，$x_2$无法成为$cel{l}_{x_1}$中的一员
• 对于$x_3$，其距离$x_2$比$x_1$近，因此，$x_3$无法成为$cel{l}_{x_1}$中的一员
• 对于$x_4$，其距离$x_2,x_3,x_5$均比$x_1$近，因此，$x_4$无法成为$cel{l}_{x_1}$的一员
• 对于$x_5$，其距离$x_2,x_3,x_4$均比$x_1$近，因此，$x_5$无法成为$cel{l}_{x_1}$的一员
  因此，$x_1$组成的$cell$为空，即$cel{l}_{x_1}=\mathrm{\varnothing }$

再考虑样本$x_2$构成的$cell$，记作$cel{l}_{x_2}$

• 对于$x_1$，由于没有任何一样比$x_2$距离$x_1$更近，因此$x_1$成为其一员
• 对于$x_3$，由于没有任何一样比$x_3$距离$x_1$更近，因此$x_3$成为其一员
• 对于$x_4$，其距离$x_3,x_5$均比$x_2$近，因此，$x_4$无法成为其一员
• 对于$x_5$，其距离$x_3,x_4$均比$x_2$近，因此，$x_5$无法成为其一员
  因此，$cel{l}_{x_2}=\{x_1,x_3\}$

同理我们可以得到$cel{l}_{x_3}=\{x_2\}$，$cel{l}_{x_4}=\{x_5\}$，$cel{l}_{x_5}=\{x_4\}$
这样一来，有所有$cell$定义的区域就组成了整个空间，就可以通过每个$cell$构成的区域中的样本来对新样本进行预测。

上面只是理想中的方式，是一种辅助理解的办法，存在诸多问题，比如区域不好定义，上面的示例中我们只是规定了一个$cell$所必须包含的元素，并没有定义由这些元素构成的区域。
在实际中，我们往往直接使用与每个样本$x$最近的$k$个样本$N_k(x)$的类别对$x$的类别进行预测，比如下面的所属表决规则。
$$\begin{array}{}\text{(1)}& y=\underset{c_j}{\arg max}\sum _{x_i\in N_{k}x}I(y_i=c_j),i=1,2,\cdots ,N;j=1,2,\cdots ,K\end{array}$$
其中$N$为全体样本，$K$为所有类别数，而距离度量往往使用L1范数，当然其他距离也行，下面是三种常见的距离。
曼哈顿距离(L1范数)：
$$\begin{array}{}\text{(2)}& L_1(x_i,x_j)=\sum _{l=1}^n|x_i^{(l)}-x_j^{(l)}|\end{array}$$

$$\begin{array}{}\text{(3)}& L_2(x_i,x_j)=(\sum _{l=1}^n|x_i^{(l)}-x_j^{(l)}{|}^2{)}^{\frac{1}{2}}\end{array}$$

$$\begin{array}{}\text{(4)}& L_{\mathrm{\infty }}(x_i,x_j)=\underset{l}{max}|x_i^{(l)}-x_j^{(l)}|\end{array}$$

三种距离在二维空间中的等距图如下：

对于$L_1$(黑色)，由于夹角$\theta =\frac{\pi }{4}$，所以黑线上的点到原点的$L1$始终相等，由于橙色为半径为1的圆，因此橙色上的点到原点的$L_2$均为半径，红色为边长为2的正方形，其上的点到原点的$L_{\mathrm{\infty }}$均为边长的一半。(图中指示错误$L_3$应改为$L_{\mathrm{\infty }}$)

kd树

从上面的介绍可知，若想找去每个样本的$k$个近邻$N_{x_k}$则需要计算$N$次后再排序选出，那么所有样本计算的时间复杂度至少是$N^2$级别，显然代价无法承受，因此需要一种能够有效减少冗余计算的方式。而$kd$树就是其中一种，它包括建树和查找两个过程。

平衡树的建立

$kd$树的建立过程比较简单，主要遵从如下思想：
假设样本为$d$维，首先取所有样本在$d=1$维度上的值并排序，找到中位数(若为偶数则计算二者均值)，取出中位数对应的样本(若不存在则在其相邻处随机取一个)建立根结点，并对左右两部分样本进行递归进行上述操作$d=(d+1)\mathrm{\%}d$

示例：
有以下二维空间中的数据集，要求建立一个$kd$树

$$T=\{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)\}$$

首先让所有样本在$d=1$维上进行从小到大的排序得到：

$$T_1=\{(2,3),(4,7),(5,4),(7,2),(8,1),(9,6)\}$$

得到中位数$=\frac{5+7}{2}=6$，但是样本中不含这个样本，因此需要在两侧附件随机取1个构建根结点，机器学习课本中选择7，这里我们以5作为示例。
因此得到$roo{t}_{T_1}=(5,4)$, $T_{11}=\{(2,3),(4,7)\}$, $T_{12}=\{(7,2),(8,1),(9,6)\}$

继续构建下一层$d=2$维上样本
对于$T_{11}$在$d=2$上进行排序得到$T_{211}=T_{11}$，计算中位数$=\frac{3+7}{2}=5$，由于$T_{211}$中不存在第二维为5的样本，因此随机选1，这里选$roo{t}_{T_{211}}=(2,3)$，因此$T_{2112}=\{(4,7)\}$成为它的右子树(同时也是右根，右叶结点)，并且无左子树。

对于$T_{12}$在$d=2$上进行排序得到$T_{212}=\{(8,1),(7,2),(9,6)\}$，计算中位数$=2$，因此得到$roo{t}_{T_{212}}=(7,2)$, 左子树(左根，左叶)$T_{2121}=\{(8,1)\}$，右子树(右根，右叶)$T_{2122}=\{(9,6)\}$。
至此，原始样本的对应的平衡$kd$树构建完毕。
下面是图例：

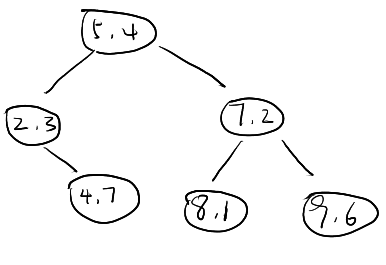
树的查找

树的查找包括正向和反向两个过程，正向和建树类似只需一一判断即可，反向也是必须的，因为正向过程不能保证所查找到的一定是其最近邻(需要参见$kd$树原始论文)。

• 正向递归查找。当给出一个样本在查找与它的最近邻样本时(限定$L_2$距离)时，需要依次从根节点往下查找，和建树过程类似，比如在建立第一层时用的是$d=1$即第一维值的大小，那么查找时也应使用样本的第一维与其第一维进行比较，该过程递归进行直至找到叶子结点。
• 反向回溯查找。在得到正向查找中与样本点$x_i$的近似最近邻点$x_j$时，以$x_i$为圆心，$x_i$到$x_j$的$L_2$距离为半径构建一个圆。回溯，依次各个区域是否与圆相交，若相交找到与其相交的最小区域对应的结点，
  示例：
  我们考虑比机器学习课本更复杂一些的情况，如下。
  
  首先我们容易根据正向查到找到样本点$S$所处的区域即B的右子树对应的区域，也是叶结点$D$的范围。构建以$S$为圆心，$d_{SD}$为半径的圆。然后检查$F$对应的区域是否与圆相交，显然不相交，于是F向上回溯至A的上半部分$C$对应的区域，显然与圆相交。于是检查C的左区域$G$对应的区域，无相交，检查$C$的右区域$E$是否相交，相交，更新半径为$d_{SE}$，并构建新圆，如下。
  

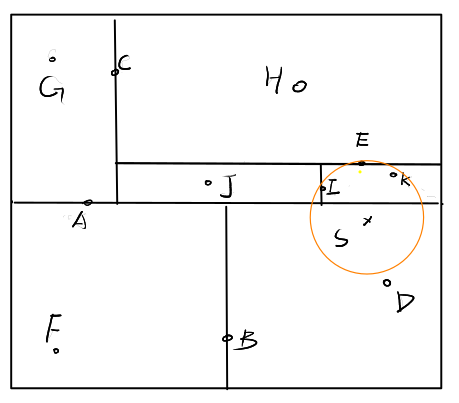
继续检查$E$的上区域$H$是否相交,相交，但是距离太远不用更新，继续检查E的下区域$I$是否相交，明显相交，且半径可以更新为$d_{IS}$，继续这样操作之后，还可以更新半径为$d_{KS}$(图没画好)，最终的得到S的最近邻点$K$。