一命通关双指针

---

双指针

简介 

双指针严格来说不是解决某一种具体问题的算法，而是对于某些场景下节省时空复杂度的优化方法。例如在以某条件遍历数组的时候，如果条件需要我们找到满足关系的两个元素，如果我们直接去遍历数组中的所有两个元素对，时间复杂度自然就上天了。
但是如果，我们可以利用某些数学关系，一边遍历一边排除，就可以节省很多时间复杂度，甚至可以压缩为只需要遍历一次。

打个比方，给一个已知升序的数组，求在这个数组中所有满足a+b=9的元素对

一般来说，如果我们暴力求解，就是枚举出所有两个元素能组成的元素对，然后依次去判断其和是否为9，时间复杂度为经典的O(n^2)
但是，但凡有一点数学功底的人都不难看出，我们可以在找的途中排除掉很多情况。比如，假设我们最开始选出的是1和5，发现1+5=6<9，很明显在5之前的1+3和1+4肯定不满足情况，我们可以直接舍弃掉。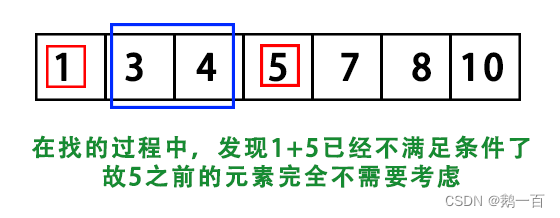

同理，如果我们先找的是4和7，那么7之后的元素我们也不需要考虑。 

既然这样，我们不妨i初始化为第一个数，j初始化为最后一个数，通过这样的初始化，i不断向后增加，j不断向前增加，此时我们可以舍弃掉大部分情况，最终时间复杂度降为了O(n) 

这便是双指针

双指针的类别

双指针大概可分为两类：

快慢指针

其中第一类，快慢指针，主要指两个指针从同一个地点出发，其中一个指针因某个条件移动更快，导致整个数组被划分为了三个区间：

比如这里，只要是个活物，fast就向后移动，但是只有是沈阳大街的，slow才向后移动；如果fast指向的元素满足slow的条件，就将nums[fast]和nums[slow]交换，这样便完成了区间划分

左右指针

而第二类，左右指针，主要是两个指针一前一后分别出发，就比如在简介中所举出的例子，便是左右指针。

---