算法笔记-第十章-图的遍历（未处理完-11.22日）

图遍历的知识点一

关于深度和广度优先遍历的基础知识 ：

大佬讲解

大佬讲解一

大佬讲解二

图遍历知识二

连通分量

算法笔记-352

DFS的具体实现
两个概念：
连通分量，强连通分量（有向路径）

实现DFS的模板思路

DFS(u)//访问顶点u
{
    vis[u] = true;
    for (从u出发能到达的所有顶点)
    {
        if vis[v] == false//如果v未被访问  
        {
            DFS(v);//递归访问v  
        }
    }
    DFStrave(G)//遍历图G  
    {
        for (G的所有顶点u)//对G的所有顶点u  
        {
            if (vis[u] == false)//如果u未被访问  
                DFS(u);//访问u所在的连通块  
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

邻接矩阵版本

//邻接矩阵版本
const int N = 1001, INF = 1000001;
int n, G[N][N];
bool vis[N] = { false };
void DFS(int u, int depth)
{
    vis[u] = true;
    //需要对u进行一些操作，从u出发
    //能到达的 分支进行枚举
    for (int v = 0; v < n; v++)
    {
        if (vis[v] == false && G[u][v] != INF)
        {
            DFS(v, depth + 1);  
        }
    }

}
void DFStrave()//遍历图  
{
    for (int u = 0; u < N; u++)  
    {
        if (vis[u] == false)  
        {
            DFS(u, 1);  
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

邻接表版本

//邻接表版
vector<int> adj[N];
int n;
bool vis[N] = { false };
void DFS(int u, int depth)
{
    vis[u] = true;
    for (int i = 0; i < adj[u].size(); i++)//从u出发可以到达的所有顶点
    {
        int v = adj[u][i];
        if (vis[v] == false)
        {
            DFS(v, depth + 1);  
        }
    }

}
void DFStrave()//遍历图  
{
    for (int u = 0; u < N; u++)  
    {
        if (vis[u] == false)  
        {
            DFS(u, 1);  
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

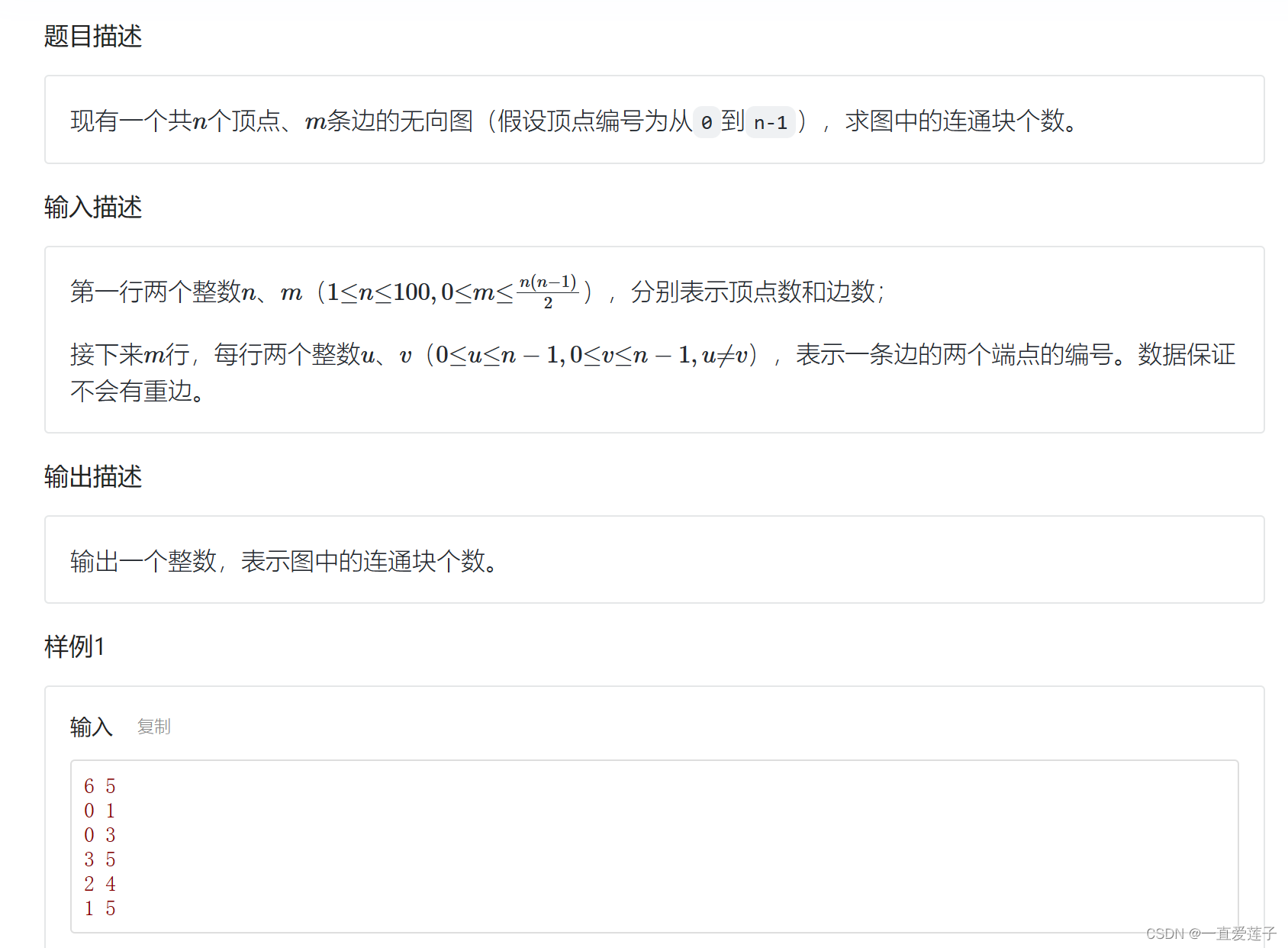
无向图的连通块