【时间序列分析】A Transformer-based Framework for Multivariate Time Series Representation Learning论文笔记

文章全名：A Transformer-based Framework for Multivariate Time Series Representation Learning

文章地址：A Transformer-based Framework for Multivariate Time Series Representation Learning | Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining

来源：KDD 2021

完成单位：Brown University，IBM Research

摘要

本文基于Transformer编码器的架构提出了一种新型的多变量时间序列的表示学习框架。

框架包含了一个无监督的预训练方案，这种无监督方法会在一些下游任务种比完全监督方法有更好的表现，并且无需利用额外的未标记数据，只需要重用已有数据即可。

经过实验发现本文的方法比当时的时间序列分析方法要更好，尤其是在回归和分类任务上，甚至训练集种只需包含几百个训练样本就能到达很好的训练效果。

这是第一个在多变量时间序列的回归任务和分类任务上达到sota的无监督方法。

简介

在大数据时代，有标签数据是很难获得的，去大量地标记数据是非常昂贵而且不切实际的。因此人们对仅使用有限量的标记数据或者是利用大量已有的未标记数据来提高精度的方法产生了很大的兴趣。

并且在当时很多深度学习模型被运用于像是CV和NLP的任务中，但是在多变量时间序列中还没有工作使用深度学习方法。

因此本文第一次使用了一种无监督的使用了Transformer编码器架构的表示学习方法来处理多变量时间序列。

Transformer能在NLP任务中表现很成功的一大原因是通过无监督预训练来学习如何表示自然语言。

Transformer中的多头自注意力机制非常适合用于时间序列分析，原因为：一方面能够关注到每个序列元素的上下文信息，另一方面多头也能够表示序列不同的子空间，比如说这可能对应于信号中的多个周期。

本文提出使用Transformer模型作为编码器来提取多变量时间序列的密集向量表示，并通过一个输入去噪（自回归）目标进行预训练。预训练模型可以用于多个下游任务，如回归、分类、填充和预测。这种方法中使用的Transformer模型参数数量最多只有数千个，可以在普通GPU上有效地训练，速度与非深度学习的方法相当。

模型

基础模型

模型只使用了Transformer的编码器结构，没有使用解码器结构，因为解码器结构适用于生成任务，尤其是对于输出序列长度没有提前给定的情况。

本文的目的是构建一个适用于多任务的通用框架，只包含编码器结构会让模型更具通用性，并且能让参数量只有原来的一半。

模型的结构图如下所示：

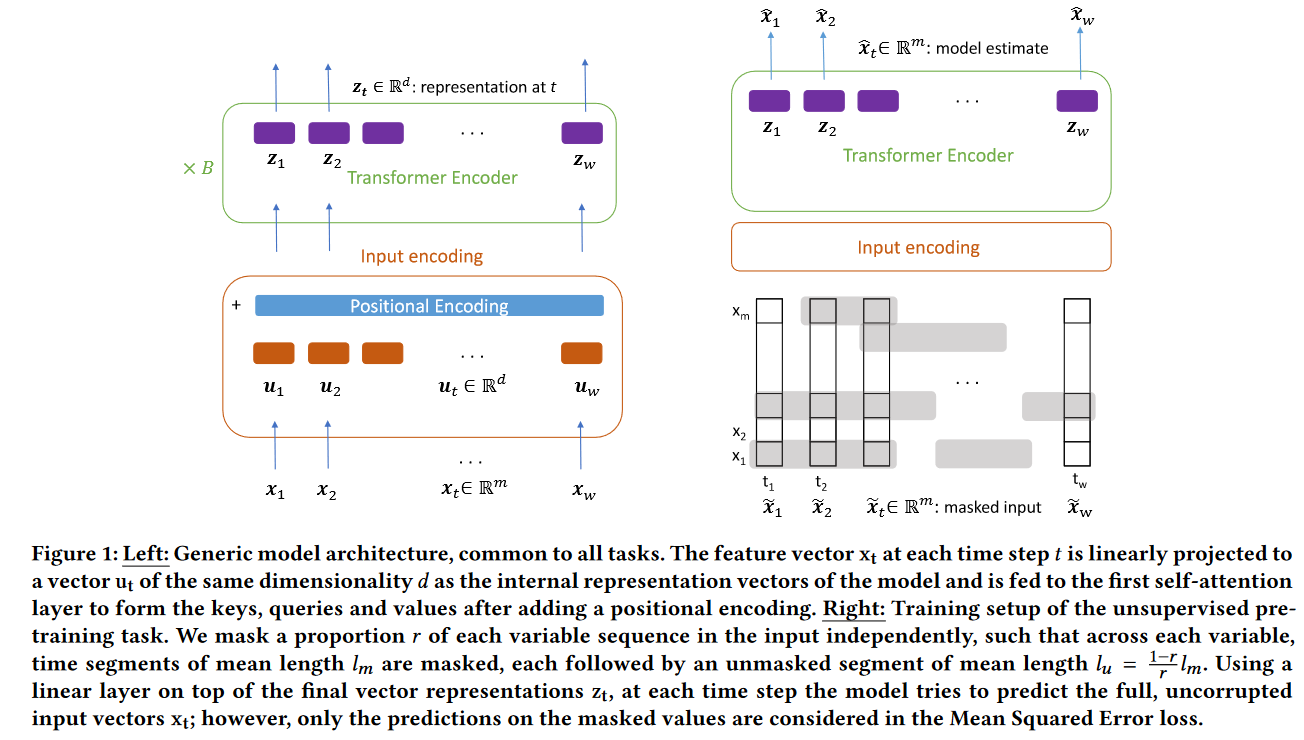
每个训练样本的维度是$X\in {\mathbb{R}}^{w\times m}$，其中$w$是序列长度，$m$是变量个数，初始的特征向量是经过标准化的，然后映射到一个$d$维的向量空间。
$$u_t=W_p{x}_t+b_p$$
其中$W_p\in {\mathbb{R}}^{d\times m}$，$b_p\in {\mathbb{R}}^d$是可学习的参数，$u_t\in {\mathbb{R}}^d$，是模型的输入向量，类比NLP任务中的词向量。这些向量将成为自注意力层的查询（queries）、键（keys）和值（values），在添加位置编码并乘以相应的矩阵后进行计算。

上述公式也涵盖了单变量时间序列的情况，即m=1，此外，输入向量$u_t$不一定需要从时间步t的（转换后的）特征向量中获取，因为模型的计算复杂度随着输入序列长度w的增加而呈现$O(w^2)$的规模，而一些参数的数量随着w的增加而呈现$O(w)$的规模，例如：可学习的位置编码、批归一化和输出层。所以在数据的粒度（时间分辨率）非常细的情况下，可以使用具有1个输入和d个输出通道，尺寸为(k,m)的卷积核$K_i$的一维卷积层来获取，其中k是时间步数，i是输出通道。
$$u_t^i=u(t,i)=\sum _j\sum _{h}x(t+j,h)K_i(j,h),i=1,\dots ,d$$
这样，可以通过使用大于1的步幅或伸缩因子来控制时间分辨率。这种方式在单变量时间序列任务中非常有效，并且适用于低维数据或是较长的序列。

由于Transformer的前馈网络对于输入顺序是不敏感的，所以为了让模型参考谢列德相对位置信息，本文使用了位置编码。
$$\begin{gathered} U^{\prime }=U+W_{pos} \\ {W}_{pos}\in {\mathbb{R}}^{w\times d} \\ U\in {\mathbb{R}}^{w\times d}=[u_1,\cdots ,u_w] \end{gathered}$$
不同于原Transformer论文提出的使用正弦函数来进行编码，本文使用了可学习的位置编码，与词嵌入的情况类似，位置编码一般不会显著干扰时间序列的数值信息；本文假设这是因为它们被学习，从而占据了一个与投影时间序列样本所在的子空间不同的、近似正交的子空间。

此外本文也考虑到每个数据样本的长度可能是不同的，所以本文设置了一个最大长度，对于短的样本使用任意值来进行填充，并且生成一个填充掩码，它为填充位置的注意力分数增加了一个很大的负值，这样模型就会忽略这些被填充的位置，同时还能让模型能够在批次中并行地处理样本。

NLP任务中的Transformer使用LayerNorm进行标准化，本文使用了Batch Normalization，从而可以减轻时间序列中异常值的影响，这是NLP任务中词向量不会出现的问题。BN在NLP任务中表现不好可能是因为每个句子间的差异很大，但是时间序列任务中这个问题就几乎没有。下表展示了BN在时间序列任务的优越性。

回归和分类

如果要将预训练模型运用于下游任务时，可将最终的表示向量$z_t\in {\mathbb{R}}^d$拼接成一个向量$\bar{x}\in {\mathbb{R}}^{d\cdot w}$，将这个作为线性输出层的输入，该层的参数为$W_o\in {\mathbb{R}}^{n\times (d\cdot w)}$，$b_o\in {\mathbb{R}}^n$，n在回归任务中设置为1，在分类任务中设置为类别数目。
$$\hat{y}=W_o\bar{z}+b_o$$
回归任务的损失函数为误差平方和，分类任务的损失函数为交叉熵损失。

本文比较了训练所有权重，和冻结所有层的参数，只训练输出层这两种情况的模型效果。

无监督预训练

本文考虑对输入进行去噪的自回归任务：具体来说，本文将部分输入设置为0，并要求模型预测屏蔽值。如figure1的右侧所示。每个训练样本和epoch独立创建一个二进制噪声掩码$\mathbf{M}\in {\mathbb{R}}^{w\times m}$，然后将输入和掩码对应位相乘$\tilde{\mathbf{X}}=\mathbf{M}\odot \mathbf{X}$，被掩盖的比例设置为$r$，$r$设置为1.5，掩盖的长度遵循几何分布，平均值为$l_m=3$，每个掩盖段后面跟着一个未掩盖段$l_u=\frac{1-r}{r}{l}_m$。之所以固定了掩盖长度是因为输入中非常短的掩蔽序列（例如，1个掩蔽元素）通常可以通过复制前面或之后的值或其平均值来进行简单的近似预测。

选择这种方式是因为它鼓励模型学习同时关注个体变量中的前段和后段，以及时间序列中其他变量的现有当前值，从而学习建模变量之间的相互依赖关系。在表3中，表明这种掩蔽方案比其他可能的输入去噪方法更有效。

$$\begin{array}{c}{\hat{\mathbf{x}}}_{\mathbf{t}}={\mathbf{W}}_{\mathbf{o}}{\mathbf{z}}_{\mathbf{t}}+{\mathbf{b}}_{\mathbf{o}}\\ {\mathcal{L}}_{\text{MSE }}=\frac{1}{|M|}\sum _{(t,i)\in M}\sum (\hat{x}(t,i)-x(t,i){)}^2\end{array}$$

M ≡ { ( t , i ) : m t , i = 0 } M \equiv\left\{(t, i): m_{t, i}=0\right\} M≡{(t,i):mt,i​=0}

$m_{t,i}$是掩码M的元素。

实验

回归任务

重要的是，本文观察到预训练的Transformer模型在6个数据集中的3个数据中优于全监督模型。这是有趣的，因为没有额外的样本用于预训练：好处似乎来自于通过一个无监督的目标重用相同的训练样本进行学习。

为了更好地阐明这个现象，本文研究了两个问题。

Q1：给定一个具有一定规模的部分标记数据集，额外的标记将如何影响性能?

随着可用标签比例的增加，全监督模型的性能都得到了提高，以及先通过无监督目标在整个训练集上预训练后再微调的相同模型。有趣的是，不仅预训练的模型优于完全监督的模型，而且这种好处在整个范围内持续存在。如figure2的左图所示。

Q2：给定一个有标记的数据集，额外的未标记样本将如何影响性能?

用于无监督学习的数据样本越多，达到(注意横轴值0只对应全监督训练,其他值都对应无监督预训练后再进行有监督微调)的误差越低。如figure2右图所示。

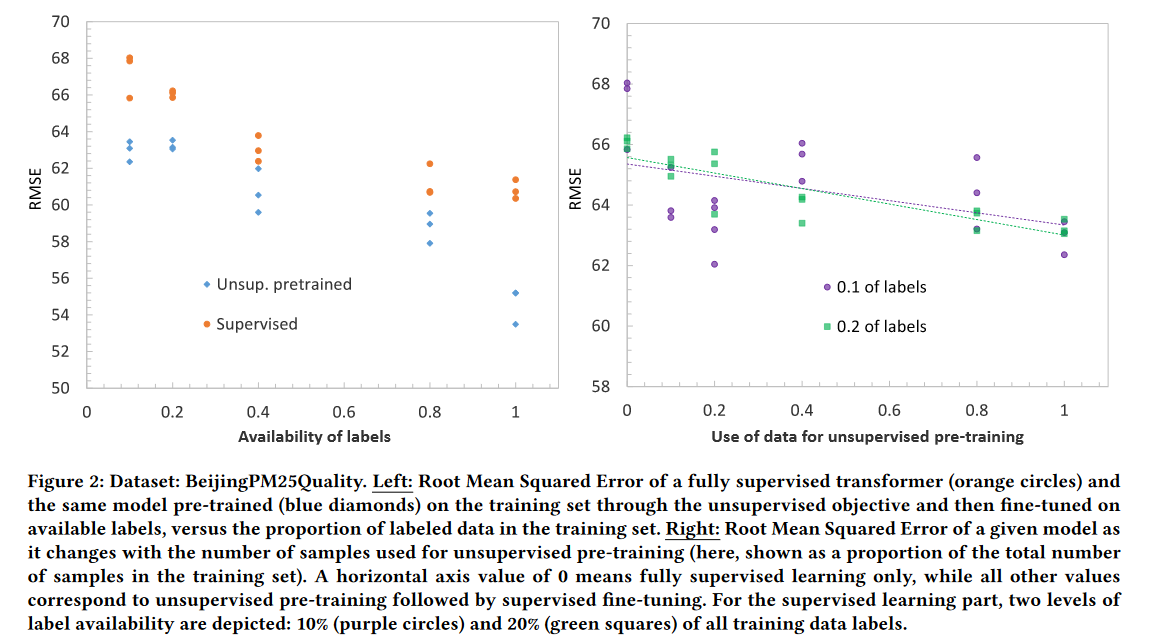
分类

目前本文模型在处理非常低维的时间序列时表现还不是很好，因此在未来的工作中作者计划使用1D卷积层来提取低维输入特征的表示。相反地，在高维数据中本文的模型表现得非常好。

在11个数据集中，预训练的Transformer模型在8个数据集上的表现优于全监督的模型。没有额外的样本用于无监督的预训练，这表明其好处来自于在不同的训练任务中仅仅重用相同的样本。

额外内容

本文模型的训练时间不长。

本文的模型可以用来进行插值，也可以用来进行预测。可以通过不同的掩蔽方式来实现不同的目标，比如同时掩蔽所有变量的最后一部分就可以进行预测。

由Transformer模型提取的表示$z_t$可以在$t$时间内进行聚合(例如平均)，并用于评估时间序列之间的相似性，聚类，可视化和任何其他在实际中使用时间序列表示的用例。Transformer提供的一个好处是，每个时间步都可以独立地处理表示；这意味着，例如，可以在时间序列的开头、中间或结尾处放置更大的权重，从而可以有选择地比较时间序列，可视化样本的时间演变，以及其他用例。