代码随想录算法训练营第23天|669. 修剪二叉搜索树 108.将有序数组转换为二叉搜索树 538.把二叉搜索树转换为累加树

JAVA代码编写

669. 修剪二叉搜索树

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：

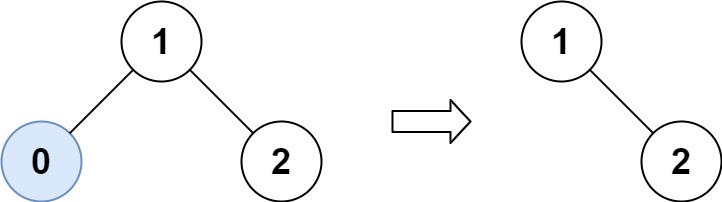
输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]
1
2

示例 2：

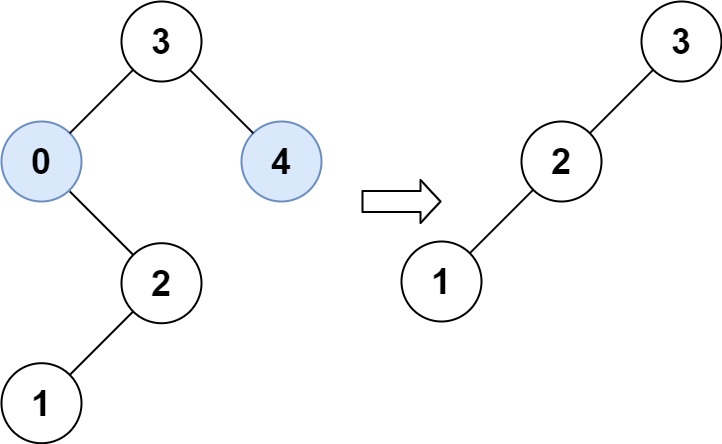
输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]
1
2

提示：

• 树中节点数在范围 [1, 104] 内
• 0 <= Node.val <= 104
• 树中每个节点的值都是 唯一 的
• 题目数据保证输入是一棵有效的二叉搜索树
• 0 <= low <= high <= 104

教程：https://programmercarl.com/0669.%E4%BF%AE%E5%89%AA%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91.html

方法一：

思路：

复杂度分析：

• 时间复杂度: O(n)，其中n是二叉搜索树中的节点数
• 空间复杂度: O(h)，h是树的高度。

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if (root == null) {
            return null;
        }
        if (root.val < low) {
            return trimBST(root.right, low, high);
        }
        if (root.val > high) {
            return trimBST(root.left, low, high);
        }
        // root在[low,high]范围内
        root.left = trimBST(root.left, low, high);
        root.right = trimBST(root.right, low, high);
        return root;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

108. 将有序数组转换为二叉搜索树

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。

高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例 1：

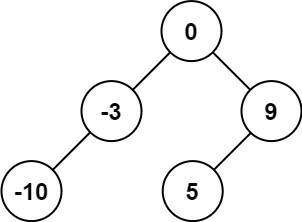
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：
1
2
3

示例 2：

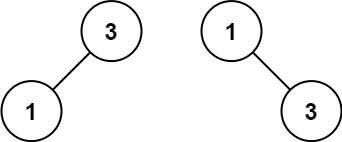
输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
1
2
3

提示：

• 1 <= nums.length <= 104
• -104 <= nums[i] <= 104
• nums 按 严格递增 顺序排列

教程：https://programmercarl.com/0108.%E5%B0%86%E6%9C%89%E5%BA%8F%E6%95%B0%E7%BB%84%E8%BD%AC%E6%8D%A2%E4%B8%BA%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91.html

方法一：

思路：

复杂度分析：

• 时间复杂度: O(n)，数组的长度为n
• 空间复杂度: O(h)，最好情况下为O(log n)，在最坏情况下为O(n)。

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return sortedArrayToBST(nums, 0, nums.length);
    }
    
    public TreeNode sortedArrayToBST(int[] nums, int left, int right) {
        if (left >= right) {
            return null;
        }
        if (right - left == 1) {
            return new TreeNode(nums[left]);
        }
        int mid = left + (right - left) / 2;
        TreeNode root = new TreeNode(nums[mid]);
        root.left = sortedArrayToBST(nums, left, mid);
        root.right = sortedArrayToBST(nums, mid + 1, right);
        return root;
    }
}


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

538.把二叉搜索树转换为累加树

• 给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

  提醒一下，二叉搜索树满足下列约束条件：

  • 节点的左子树仅包含键 小于 节点键的节点。
  • 节点的右子树仅包含键 大于 节点键的节点。
  • 左右子树也必须是二叉搜索树。

  **注意：**本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同

  示例 1：

  

  输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
  输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
  1
  2

  示例 2：

  输入：root = [0,null,1]
  输出：[1,null,1]
  1
  2

  示例 3：

  输入：root = [1,0,2]
  输出：[3,3,2]
  1
  2

  示例 4：

  输入：root = [3,2,4,1]
  输出：[7,9,4,10]
  1
  2

  提示：

  • 树中的节点数介于 0 和 104 之间。
  • 每个节点的值介于 -104 和 104 之间。
  • 树中的所有值 互不相同 。
  • 给定的树为二叉搜索树。

教程：https://programmercarl.com/0538.%E6%8A%8A%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E8%BD%AC%E6%8D%A2%E4%B8%BA%E7%B4%AF%E5%8A%A0%E6%A0%91.html

方法一：

思路：

复杂度分析：

• 时间复杂度: O(n)，数组的长度为n
• 空间复杂度: O(h)，h是高度。

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {
    int sum;
    public TreeNode convertBST(TreeNode root) {
        sum = 0;
        convertBST1(root);
        return root;
    }

    // 按右中左RDL顺序遍历，累加即可
    public void convertBST1(TreeNode root) {
        if (root == null) {
            return;
        }
        convertBST1(root.right);
        sum += root.val;
        root.val = sum;
        convertBST1(root.left);
    }
}


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34