SynCoBERT：语法引导的多模态对比预训练用于代码表示。

Introduction

代码表示学习（也称 code embedding）旨在将源代码的语义编码为分布式向量，在最近基于深度学习的代码智能模型中起着重要作用。

存在问题

• 为了更好地表示代码的语法结构，考虑源代码的两个关键但被忽视的特征：
  1. Code identifier 包含了符号和语法的信息。标识符 identifier 和变量是程序设计语言的基本组成部分。它不应该被简单地视为常规的文本代码标记。例如，给定表达式 x = len(“x”)，前面的 x 是一个 identifier，它可以区分后面的字符串 x，标识符在理解代码逻辑方面起着重要的作用，因为它们包含了关键的符号和语法信息。
  2. AST 边的语法信息被忽略。下图显示了一个带有 AST 的Python代码片段。在这个AST中，一个二进制操作符语句 x + y 可以由一个指向三个叶子节点（x，y和一个操作符 +）的非叶子节点 binary-operator 表示。我们认为连接非叶节点和叶节点的边包含了丰富的句法结构信息，这些信息应该被考虑在内。
     
• 程序通常由代码片段和相应的注释组成。一个代码片段可以被解析成一个或多个语法结构(例如，AST或控制/数据流图)。在本文中，我们从不同的角度将这些代码特征称为代码的多模态。我们认为，这些语义等效的模式提供了互补的信息，以学习更全面的代码表示。然而，以前的工作并没有进一步探索不同形式的代码之间潜在的相互信息。

主要贡献：

• 提出了SYNCOBERT，一个语法引导的多模态对比预训练框架，用于代码表示。我们设计了两个新的预训练目标来编码编程语言的符号和语法信息。第一个IP目标预测代码token是否是标识符。第二个TEP目标预测AST的两个节点之间的边。
• 提出了一种多模态对比预训练策略，该策略通过对比学习来学习更全面的表征，从而最大化不同模态(代码、注释和AST)之间的相互信息。

SynCoBERT

1 Preliminary

输入表示：将代码的AST作为模型输入的一部分，该模型提供了一个具有深度优先遍历的 AST token 序列。下图展示了从图1中的 AST 中获得的部分 AST 序列示例。蓝色箭头表示节点之间的边。

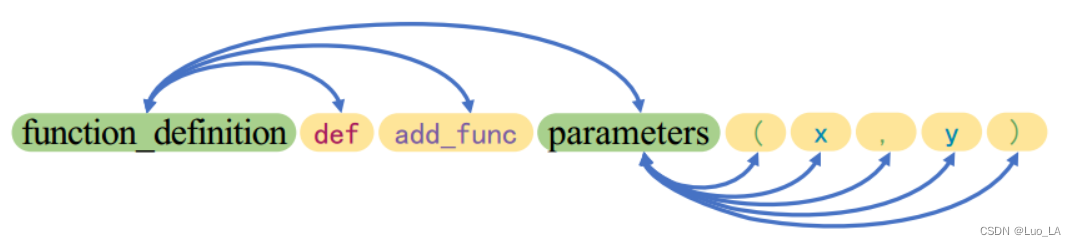
给定一个自然语言注释 $w=w_1,w_2,...,w_{|w|}$，其对应的源代码 $c=c_1,c_2,...,c_{|c|}$，对应的 AST 序列 $a=a_1,a_2,...,a_{|a|}$，SynCoBERT采用多模态（NL，PL，AST）的连结作为输入，即：

其中 [CLS] 是”分类任务“的特殊 token，出现在输入序列的开头。[SEP] 是分隔两种子序列的特殊 token。

模型结构：构建在多层 Transformer 编码器上。

2 Multi-Modal Masked Language Modeling (MMLM)

给定一个 NL-PL-AST 三元组 { w , c , a } \{w,c,a\} {w,c,a} 数据点作为输入。我们从NL、PL 和 AST 的连接中随机选择15%的令牌。用[MASK]令牌替换其中的80%，用随机令牌替换10%，其余10%不变。MMLM的目标是预测 masked tokens 的交叉熵损失:

其中 $M=w^m\cup c^m\cup a^m$ 是 NL ($w^m$)，PL ($c^m$) 和 AST ($a^m$) 中的 masked tokens 集合。V 表示词表大小。$y_i^{MMLM}$ 表示 masked token $i$ 的标签，$p_i^{MMLM}$ 表示 token $i$ 的预测概率。

3 Identifier Prediction (IP)

标识符(identifier)作为一种典型的符号，在源代码中起着重要的作用。它可以被另一个字符串替换，而不会影响源代码的逻辑。考虑到标识符的重要性和所占的比例较大，我们将代码 token 类型分为标识符和非标识符。

与MMLM(预测15%的 code token)不同，我们对所有 code token 提出了标识符预测目标。对于源代码中的每个 token，如果它是标识符，则应用标签1，否则应用标签0，如图3所示。IP损失函数为二值分类损失定义为:

其中 $p_i^{IP}$ 是第 $i$ 个 code token 预测为 标识符的概率，$y_i^{IP}$ 是 第 $i$ 个 code token 的标签。

4 AST Edge Prediction (TEP)

在将AST树转换为序列时，可能会丢失一些关键的结构信息。受GraphCodeBERT中提出的数据流图的 edge masking 技术的启发，设计了 AST edge prediction 目标。以图3的 token ”result“ 为例，token（“assignment”、“result”）之间有一条边，token（“result”、“=”）之间没有边。为了整合这样的树结构信息，我们在AST中 mask edges，并要求模型预测这些 edges。该TEP目标的损失函数定义为:

其中，$N_a$ 表示 所有的 AST 节点 pairs 的集合。如果第 $i$ 个节点和 第 $j$ 个节点之间有边， $y_{(i,j)}^{TEP}$ 的值为1，否则为0。$p_{(i,j)}^{TEP}$ 是第 $i$ 个节点和 第 $j$ 个节点之间是否有边的概率，由两个节点的点击来表示。使用激活函数 sigmoid 来归一化 $p_{(i,j)}^{TEP}$ 的值，使其处于 0 到 1 之间。

5 Multi-Modal Contrastive Learning (MCL)

多模态对比学习

之前的工作已经表明，来自BERT的原生句子表示是由高频的 tokens 主导的。这种 token-imbalance 问题在代码中更为严重。以Python语言为例， ”def“ token几乎在所有函数中都会出现。

对比学习鼓励原始序列的表示更接近 ”positive“ 增广序列的表示，同时远离 ”negative“ 序列的表示，让模型在不同点之间学习更均匀的决策边界，以调整由于 token imbalance 造成的偏差。

最近的一些工作尝试去对比代码片段的相似处和不相似处。然而，它们只处理代码的单一模态，而忽略了编程语言的多模态特性。这些语义等价的模态可以提供补充信息，以学习更全面的代码表示。因此提出多模态对比学习。

我们使用成对数据和非成对数据来训练SYNCOBERT。成对数据是指带有配对的自然语言注释(NL)的代码(PL)，非成对数据是指没有配对自然语言注释的独立代码。接下来，我们将解释如何为这两种情况构建正（positive）样本和负（negative）样本。

Positive Samples：

成对数据：

1. NL vs PL-AST：为了弥合自然语言注释与其对应的代码片段之间的 差距，我们将注释（NL）视为包含相应代码和AST的正样本。NL & PL-AST 组成了一个 positive pair，例如下图左侧中的 $x_1$ 和 $x_1^{+}$ 。
2. NL-PL-AST vs NL-AST-PL：为了更好地了解在同一NL注释条件下PL和AST之间的语义等价性，我们提出通过交换输入 input triplet 中 PL（c）和 AST（a）的顺序来构建另一组正样本，即 { w , c , a } \{w,c,a\} {w,c,a} 变成 { w , a , c } \{w,a,c\} {w,a,c}。在这个交换操作之前，原始的 input triplet 首先被不同的随机种子 mask，这是为了增加 positive pairs 之间的差异。下图右侧展示了这些步骤。
   
   非成对数据

考虑 PL-AST vs AST-PL 来构建正样本。该方案的工作原理与上面介绍的 NL-PL-AST vs NL-AST-PL 的设置相同（不考虑 NL）。

Negative Samples

为获取 MCL 负样本，采用 in-batch 和 cross-batch 采样方法。

对于批次大小为N的训练数据 $b_1=[x_1,...,x_N]$，我们可以首先使用前面描述的方法获得另一批大小为N的 positive data batch $b_2=[x_1^{+},...,x_N^{+}]$，其中 { x i , x i + } \{x_i,x_i^+\} {xi​,xi+​} 是 positive pair。对于 $x_i$，in-batch 和 cross-batch 的负样本为 { x j } , j ≠ i \{x_j\}, j ≠i {xj​},j=i，这样，对于每个 $x_i$，我们可以得到 2N-2 个负样本的集合 $X^{-}$，如下图所示。

Overall MCL Pipeline

对于成对数据中的输入 $x_i$ ，我们执行以下步骤（非成对数据类似）：

• 首先，按照前面介绍的两种方法为 $x_i$ 构造一个正样本 $x_i^{+}$。

• 将 $x_i$ 和 $x_i^{+}$ 作为 SynCoBERT 的输入，然后我们可以得到它们的向量表示 $h_i=SynCoBERT(x_i)$ 和 $h_i^{+}=SynCoBERT(x_i^{+})$

• 最后，采用一个两层的 MLP $f(.)$ ，它将表示映射到空间 $v_i=f(h_i),v_i^{+}=f(h_i^{+})$，其中应用了对比损耗。通过非线性变换， $h$

  中可以保留更多的信息。

对于表示为 $v_i$ 的输入 $x_i$ , 他有一个表示为 $v_i^{+}$ 的正样本 $x_i^{+}$ , 它也有一组大小为 2N-2 的负样本。我们将 $X^{-}$ 中样本的表示为 V − = { v 1 − . . . v 2 N − 2 − } V^-=\{v_1^-...v_{2N-2}^-\} V−={v1−​...v2N−2−​}，对比学习的目标是最大化正样本之间的表示相似度，同时最小化负样本之间的表示相似度。因此，我们将 positive pair ( $x_i$, $x_i^{+}$) 的损失函数定义为：

其中，一对样本的相似度由其表示的点积定义，即 $v_i\cdot v_j$

我们对同一对数据计算两次损失，即 ( $x_i$, $x_i^{+}$) 变成 ( $x_i^{+}$, $x_i$) ，因为 $x_i$ 和 $x_i^{+}$的负样本的点积是不同的。

总体 MCL 损失定义如下：

6 Training Objective

SynCoBERT的整体损失函数是之前定义的几部分的和：

其中 $\Theta$ 包含模型的所有可训练参数。$\lambda$是 $L_2$ 正则化系数，用于防止过拟合。

地址

https://arxiv.org/abs/2108.04556
Comments: 9 pages, 3 figures, 5 tables
Subjects: Computation and Language (cs.CL); Artificial Intelligence (cs.AI); Programming Languages (cs.PL)
Cite as: arXiv:2108.04556 [cs.CL]