编译原理（1）----LL(1)文法（首符号集，后跟符号集，选择符号集）

目录

1.首符号集（First()）

2.后跟符号集（Follow（））：只针对非终结符

3. 选择符号集:Select(A->)

4.构造LL(1)分析表

5.输入串的分析

---

1.首符号集（First()）

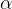技巧：找最左边可能出现的终结符

例：

1.First(E)

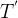E->T,最左边为T，又因为T->F,最左边为F，F->(E)|i,则最左边为{（，i }

2.First(T):只需要看符号串最左边的符号，即=First（T）

T->F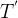，最左边为F，F->(E)|i,则最左边为{（，i }

3.First（（E））：也只需要看最左边的

   First((E))={ ( }

4.First(i):终结符的first集就是它本身

First(i)={i} 

其他以此类推：

2.后跟符号集（Follow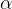（））：只针对非终结符

技巧：看”->“的右边，找出非终结符后面所能跟随的所有终结符

1. #  Follow (S),S为识别符号，即 ”#“要放在开始符号"S"的 Follow集中

2.若存在规则U->xWy,First(y)-{}（空串） Follow(W)

3.若存在规则U->xW或U->xWy,其中y能广义推导出（空串），则Follow(U)Follow(W)

Follow(E)

首先E是开始符号，Follow(E)={#}

在"->"右边找E，看E后面跟的所有终结符号,这里F->(E)| i,E的右边为"）",终结符的First集就是它本身（对应第二条规则）

所以Follow（E）={#，）}

 Follow(T)

首先找”->“的右边，看T后面跟的所有终结符号

E->T        ->+T|

T后面跟的是，的First集是{+，},将去掉，最后得到{+},又因为可以推导出空串（对应第三条规则），就要把

E->T        ->+T|    ”->“左边的E和的follow集写上

Follow（T）={+，#，）}

 Follow（E'）

首先找”->“的右边，看E’后面跟的所有终结符号

E->T        ->+T|

后面没有符号，的follow集就是”->“左边E和的follow集

Follow（）={#，）}

以此类推：

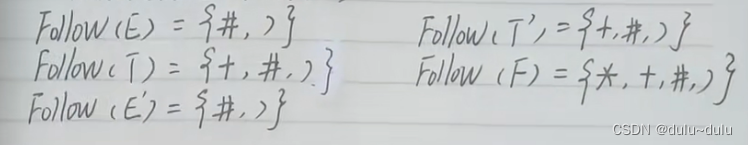
总结

 在"->"右边寻找需要求的非终结符，如果非终结符后面是终结符号，直接放到follow集中，如果非终结符后面是非终结符，就看非终结符的first集内容是什么，如果有（空串）

1.那么将空串去掉写入follow集中

2.并且将”->“左边的非终结集的follow集也写入该follow集中

例题：

3. 选择符号集:Select(A->)

约束：有两条或两条以上产生式才算可选集

E->TE'        不用算可选集

E‘->+TE'|        算可选集

规则： 

Select (E'->+TE')

根据规则，不能广义推导出，那么运用第一条规则

Select (E'->+TE')={+}

Select(E'->) 

运用第二条规则，”->“右边的首符号集-空串（这里-" role="presentation" style="position: relative;">$$后为空集），再并上E’的follow集

Select(E'->) ={#，）}

Select(T'->+FT')

”+"号的首符号集就是”+“,所以

 Select(T'->+FT')={+}

以此类推：

4.构造LL(1)分析表

以例题的形式展开：

接下来构造LL(1)分析表，行表示终结符，列表示非终结符

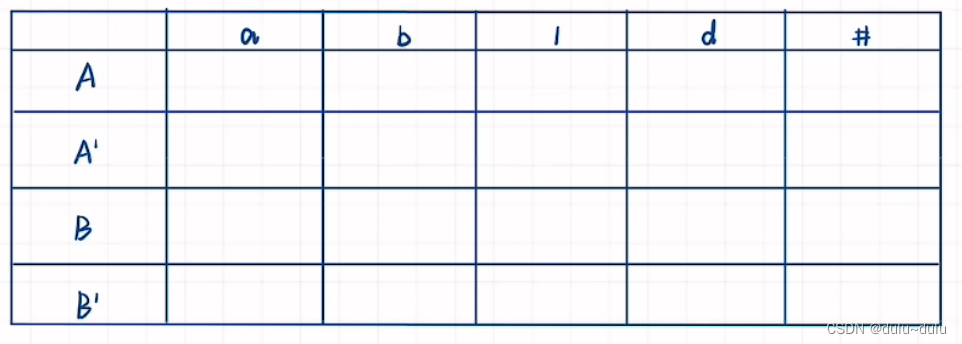
由于FIRST(A)={a}，所以：

FIRST(A')={a,}，因为A'能推出，所以要到follow中看，folllow（A’）={#，d},所以将A'->,写到其中：

以此类推，得到最终的分析表：

如何判断是否为LL（1）文法：

A-->

: 

：

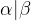
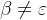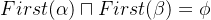
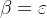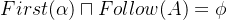
其实这中间包含了求select集的过程:

对于A-->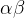而言：

若 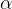是终结符，则SELECT（A）=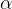

若 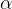是非终结符，则SELECT（A）=FIRST()

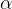对于A-->：

 SELECT（A）=FOLLOW（A）

这里判断A-->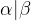是否为LL（1）文法，原理和上面是一模一样的

所以流程： ①消除左递归，消除回溯-->②计算FIRST集和Follow集--->③判断是否为LL(1)文法

5.输入串的分析

给出输入串 aad1#的分析过程

由于A->aA'，反向写入符号栈中

此时符号栈的最顶层“a”,与当前输入符号“a”相同，所以可以消去

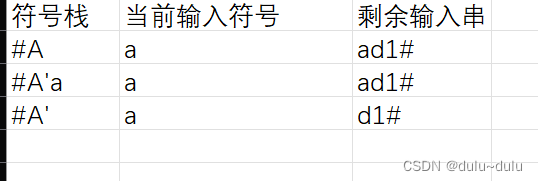
A‘->AB1|,不能写空串，这样符号栈就为了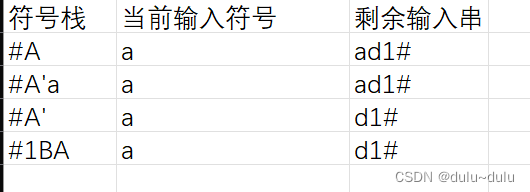

以此类推：

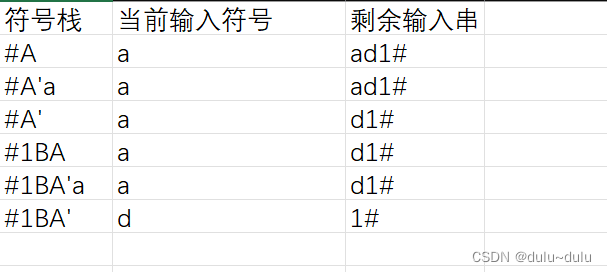
到这上面这一步，因为A’不能推出d，又因为A‘->AB1|,所以这里用A’-->,将A‘消除

现通过完整的题目练习一下:

表达式文法为：

E-->E+T|T

T-->T*F|F

F-->i|(E)

（1）消除左递归

E-->TE'

E'-->+TE'|

T-->FT'

T'-->*FT'|

F-->i|(E)

预测分析表：

字符串得分析过程：