-
【EMD】1.初识经验模态分解EMD
/** * @project 经验模态分解及其衍生算法的研究及其在语音信号处理中的应用 * @author jUicE_g2R(qq:3406291309) * * @language MATLAB/Python/C/C++ * @EDA Base on matlabR2022b * @editor Obsidian(黑曜石笔记软件) * * @copyright 2023 * @COPYRIGHT 原创学习笔记:转载需获得博主本人同意,且需标明转载源 */- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
EMD优势:自适应性
1 定义
经验模态分解(EMD) 是处理 非线性、 非平稳信号 的 时频分析方法。
该方法可以在不需要知道任何先验知识的情况下,依据输入信号自身的特点,自适应地 将信号分解成若干个本征模态函数(IMF)之和。2 应用背景
处理 非平稳信号的局部频谱分析
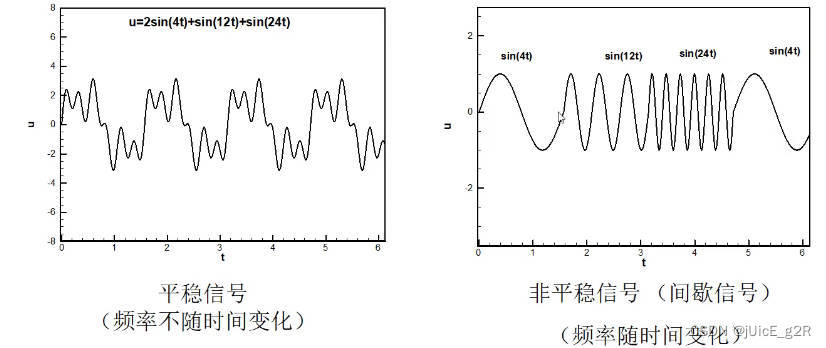
3 E M D EMD EMD 提出人黄锷 指出
频谱分解:将信号分解成不同频率的成分
-
信号
=
高频成分
+
.
.
.
+
中频成分
+
.
.
.
+
低频成分
信号=高频成分+...+中频成分+...+低频成分
信号=高频成分+...+中频成分+...+低频成分

出现极值点次数 多 的局部为 高频部分
出现极值点次数 少 的局部为 低频部分4 本征模态函数 I M F IMF IMF
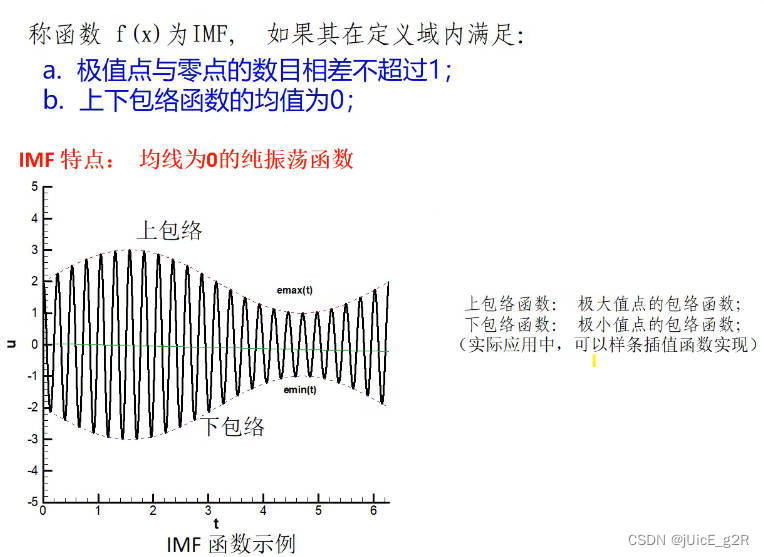
5 u ( t ) = ∑ i m f + r N ( t ) u(t)=∑imf+r_N(t) u(t)=∑imf+rN(t)
- 将
I
M
F
函数
IMF函数
IMF函数 从原来的
u
(
t
)
函数
u(t)函数
u(t)函数上 偏移到 (无限接近)
x
轴
x轴
x轴
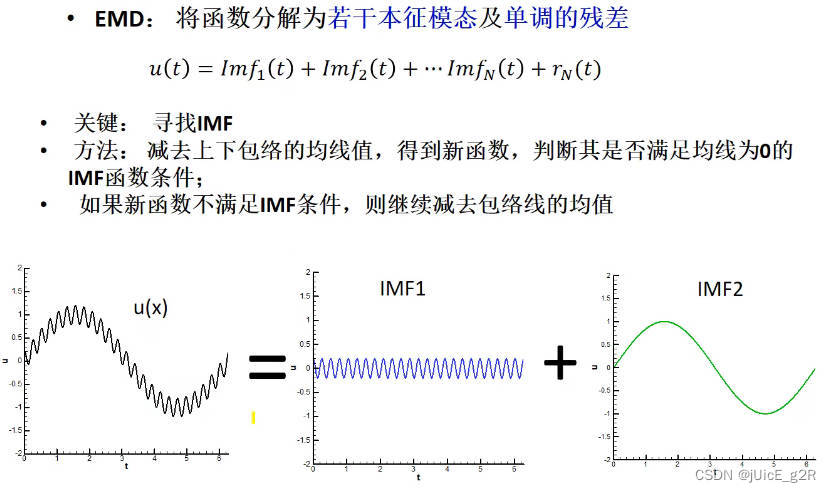
6 I M F IMF IMF的实现( S h i f t i n g Shifting Shifting算法)
6-1 S h i f t i n g Shifting Shifting算法 理论处理方案
- 红色虚线 为 上包络线(平滑的 极大值点 的连线)
- 紫色虚线 为 下包络线(平滑的 极小值点 的连线)
- 绿色实线 为 平均线(折中上、下包络线)
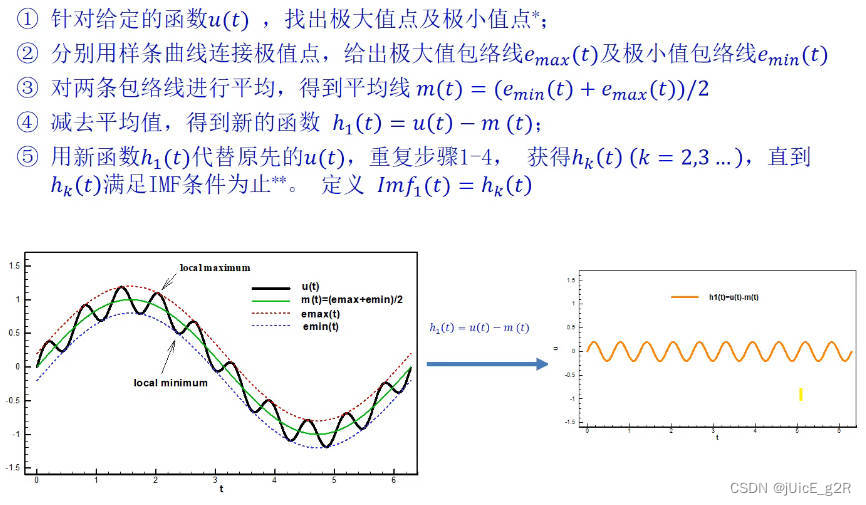
6-2 实际操作时处理极限的方案
-
h
k
(
t
)
)
h_k(t))
hk(t)) :第 k 个 中线 无限接近于
x
轴
x轴
x轴 的函数

一个 逼近值 a n 逼近值a_n 逼近值an 越接近 极限(理论)值 a ∞ 极限(理论)值a_∞ 极限(理论)值a∞,它与 上一个逼近值 a n − 1 a_{n-1} an−1 的差值越小
7 注意:端点的处理
镜像处理法

经过镜像沿拓后,上图的端点 是 极小值点 则判断该端点为 极小值点
8 基本步骤
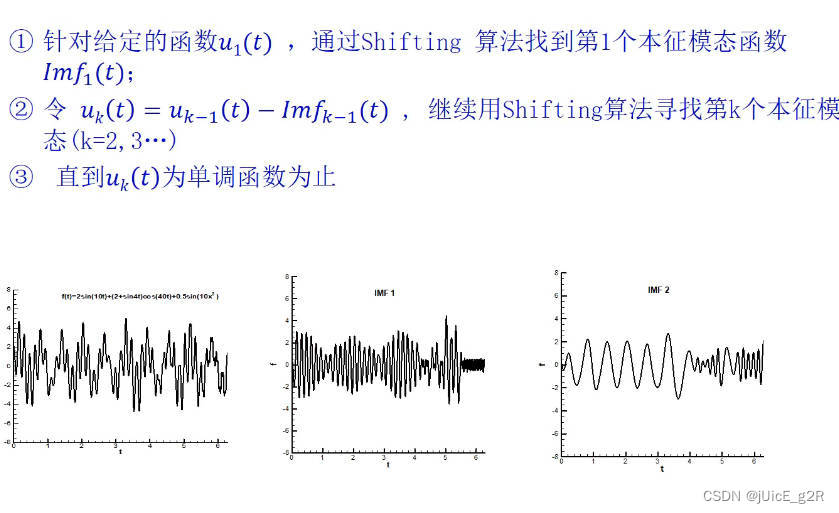
9 M a t l a b Matlab Matlab 中 E M D EMD EMD 的使用

10 实例演示

10-1 步骤
- 1、找到所有的 极值点
- 2、 样条插值法 样条插值法 样条插值法 获取到 上、下包络线 的函数
- 3、求 上、下包络线函数 的平均函数 m ( t ) m(t) m(t)
- 4、使用 S h i f t i n g 算法 Shifting算法 Shifting算法
10-2 逐步处理

11 E M D EMD EMD 的应用
11-1 在 滤波与去噪 中的应用
-
背景
传统的利用 傅里叶变换 的 频谱分析技术 对于 平稳信号 的处理很有效,但在实际生活中 平稳信号 出现的概率很小,且 傅里叶变换 对于 非平稳信号 的处理很乏力。 -
基于 小波变换的多分辨性
可以使 非平稳信号中 的 有效成分和噪声 各自呈现出不同的特征。利用信号和噪声在多尺度空间中传递特性的不同可以获得干扰背景下的有效检测。但 小波基的选取 对去噪效果有很大影响,因此基于 小波去噪 的方法 缺乏自适应性 。 -
E M D EMD EMD 的 优势:弥补 小波去噪 缺乏 自适应性 的缺点
首先,它具有良好的 局部适应性
其次,它被认为是 在继承了传统的 傅里叶变换 与 小波去噪 的优势的基础上的突破
11-2 在 信号检测 中的应用
在 信号检测 的过程中,不仅要考虑 信号的形式 和 干扰的性质,选择合适的信号处理方法 也十分重要。针对 不同的情况 寻求最优的信号处理技术 是 信号处理与检测中的核心问题之一。
本节图片参考源:经验模态分解技术-EMD-李新亮_哔哩哔哩_bilibili
参考文献:EMD算法研究及其在信号去噪中的应用_王婷.caj(第一章) -
相关阅读:
LeetCode—1. 两数之和—python
Flux脚本语言基础使用-数据类型(InFluxDB 查询语言)
进程状态和Linux的进程状态
郝斌 数据结构源代码和数据结构 大纲源代码
在上一篇文章的基础上,增加“刷新页面,使form表单数据不发生变化”
数据隐私新篇章:Facebook如何保护用户信息
ARC121E Directed Tree
【组件传参】返回e和传入的参数 - uniapp中this.$emit回传多个值 - uniapp组件中带事件参数event和多个参数
shell 中单引号,双引号,反引号的区别
docker install kafka
- 原文地址:https://blog.csdn.net/qq_73928885/article/details/134257689