【优选算法系列】第二节.双指针（202. 快乐数和11. 盛最多水的容器）

作者简介：大家好，我是未央；

博客首页：未央.303

系列专栏：优选算法系列

每日一句：人的一生，可以有所作为的时机只有一次，那就是现在！！！！！

文章目录

前言

一、202. 快乐数

1.1 题目描述

2.2 题目解析

2.2.1 算法原理

2.2.2 代码编写

二、盛最多水的容器

2.1 题目描述

2.2 题目解析

2.2.1 算法原理

2.2.2 代码编写

总结

---

---

前言

---

一、202. 快乐数

1.1 题目描述

描述：

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

• 对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
• 然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
• 如果这个过程 结果为 1，那么这个数就是快乐数。

如果 n 是 快乐数 就返回 true ；不是，则返回 false 。

---

提示：

• 1 <= n <= 2^31 - 1

---

示例1：

---

示例2：

---

2.2 题目解析

2.2.1 算法原理

题目分析：

为了方便叙述，将「对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和」这一个操作记为X操作;

题目告诉我们，当我们不断重复×操作的时候，计算一定会「死循环」，死的方式有两种:

• 情况一:一直在1中死循环，即1 ->1 ->1 ->1.
• 情况二:在历史的数据中死循环，但始终变不到1

由于上述两种情况只会出现一种，因此，只要我们能确定循环是在「情况一」中进行，还是在「情况二」中进行，就能得到结果。

---

简单证明：

a、经过一次变化之后的最大值9^2 * 10 = 810 (2^31-1=2147483647。选一个更大的最大9999999999 )，也就是变化的区间在[1，8107]之间;

b.根据「鸽巢原理」,一个数变化811次之后，必然会形成一个循环；

c.因此，变化的过程最终会走到一个圈里面，因此可以用「快慢指针」来解决。

---

解题方法：快慢指针

算法思路：
根据上述的题目分析，我们可以知道，当重复执行X的时候，数据会陷入到一个「循环」之中。而「快慢指针」有一个特性,就是在一个圆圈中，快指针总是会追上慢指针的，也就是说他们总会相遇在一个位置上。

如果相遇位置的值是1，那么这个数一定是快乐数;

如果相遇位置不是1的话，那么就不是快乐数。

---

解题步骤：

1. 初始化快慢指针，快指针。其中慢指针指向n，快指针指向n的下一位。
2. 创建一个函数实现求一个数n每个位置上的数字的平方和。
3. 使用while循环，每次循环中，慢指针计算一次平方和，快指针计算两次平方和。
4. 在每次循环中，判断慢指针和快指针的值是否不相等并且是否为1，如果不相等并且不等于1，则进入循环遍历。
5. 当同时满足相等且等于1时候，则跳出循环。则该数为快乐数，返回true；否则返回false。

---

补充知识:如何求一个数n每个位置上的数字的平方和。

a．把数n每一位的数提取出来:

循环迭代下面步骤:

1.  int t = n % 10提取个位;

2.  n /= 10干掉个位;

直到n的值变为0;

b.提取每一位的时候，用一个变量tmp记录这一位的平方与之前提取位数的平方和

tmp = tmp + t *t

代码示例：

public int calculateSquareSum(int n) {
    int tmp = 0;
    while (n > 0) {
        int t = n % 10; // 取出最低位的数字
        tmp += t * t; // 平方并累加到 sum 中
        n /= 10; // 去掉最低位的数字
    }
    return tmp;
}

举例解析：

（1）在该函数中，我们使用了一个 while 循环来迭代计算每个位上数字的平方和，直到 n 变为 0首先，我们定义一个变量 tmp，用于累加每个位上数字的平方。然后，在 while 循环中，我们使用 n % 10 来取出 n 的最低位的数字。

例如，对于数字 123，取模运算 123 % 10 的结果为 3。

（2）接下来，我们将最低位的数字平方并累加到 tmp 中，使用 tmp += t * t 这个语句实现。例如，对于数字 3，平方结果为 9，将其累加到 tmp 中。

（3）然后，我们使用 n /= 10 的语句将 n 除以 10，去掉最低位的数字。

例如，对于数字 123，n /= 10 的结果为 12。

（4）最后，当 n 变为 0 时，说明所有位上的数字都已经计算完毕，我们将 tmp 返回。

---

2.2.2 代码编写

代码解析：

---

二、盛最多水的容器

2.1 题目描述

描述：

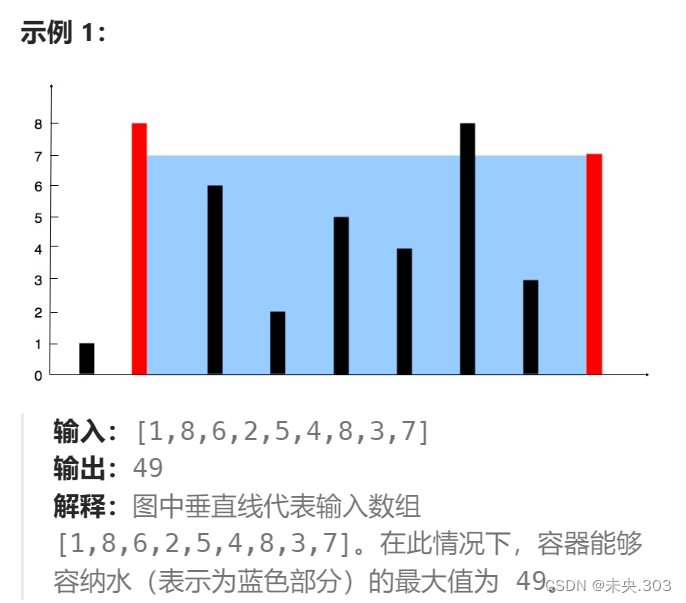
给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

---

说明：你不能倾斜容器。

---

示例1：

---

示例2:

---

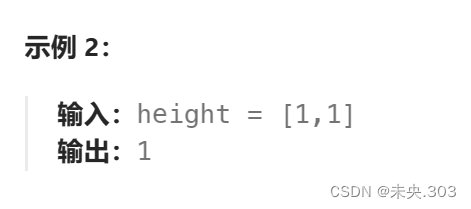
2.2 题目解析

2.2.1 算法原理

算法思路：对撞指针

设两个指针left,right分别指向容器的左右两个端点，

则此时容器的容积:v = (right - left) * min( height[right], height[left])；

容器的左边界为height[left]，右边界为height[right]。

---

我们假设「左边边界」小于「右边边界」。

分析可知如果此时我们固定一个边界，改变另一个边界，水的容积会有如下变化形式:

那么无论我们将left指针向右移动一位，还是将right指针向左移动一位，容器的宽度都会减少。而我们的目标是找到最大的容器，所以应该移动较小的柱子，以期望获得更高的柱子。

（1）如果我们移动较大的柱子，容器的宽度会减小，而高度不会有所改变，所以容器的容量也会减小。

（2）而如果我们移动较小的柱子，容器的宽度减小，而高度有可能增加，所以容器的容量有可能会增加。（高度增加的比宽度减小的多）

因此，在盛水最多的容器问题中，当height[left]小于height[right]时，我们将left指针向右移动一位；反之，我们将right指针向左移动一位。

这样我们保留了可能更高的柱子，同时也保留了可能更大的容器宽度，从而有机会找到更大的容器。

当我们不断重复上述过程,每次都可以舍去大量不必要的枚举过程，直到left与right相遇。期间产生的所有的容积里面的最大值，就是最终答案。

---

解题步骤：

步骤一：定义两个指针left和right，分别指向容器的两端。

步骤二：初始化最大容积maxArea为0。

步骤三：使用while循环，判断left小于right时执行以下操作：

1. 计算当前容积area，即min(height[left], height[right]) * (right - left)。
2. 如果当前容积大于maxArea，则更新maxArea。
3. 如果height[left]小于height[right]，则将left指针向右移动一位；否则，将right指针向左移动一位。（即将较小的一段进行移位）

步骤四：循环结束后，返回maxArea作为结果。

---

2.2.2 代码编写

代码解析：

---

总结