【机器学习可解释性】3.部分依赖图

机器学习可解释性

• 1.模型洞察的价值
• 2.特征重要性排列
• 3.部分依赖图
• 4.SHAP 值
• 5.SHAP值的高级使用

正文

每个特征怎么样影响预测结果？

部分依赖图 Partial Dependence Plots

虽然特征重要性显示了哪些变量对预测影响最大，但部分依赖图显示了特征如何影响预测。
这对于回答以下问题很有用：

• 控制所有其他房屋特征，经度和纬度对房价有什么影响? 重申一下，同样大小的房子在不同地区会如何定价?
• 预测两组之间的健康差异是由于饮食的差异，还是由于其他因素?

如果您熟悉线性或逻辑回归模型，可以将部分依赖图解释为与这些模型中的系数。
然而，复杂模型上的部分依赖图比简单模型上的系数可以捕获更复杂的样式。
如果你不熟悉线性或逻辑回归，也不要担心这个比较。

我们将展示几个示例，解释这些图的含义，然后通过代码来实现这些图。

它是如何工作的

像排列重要性一样，部分依赖图是在模型拟合后计算的。该模型适用于没有以任何方式人为操纵的真实数据。

在我们的足球例子中，球队可能在许多方面有所不同。他们的传球次数，射门次数，进球次数等等。乍一看，似乎很难理清这些特征的影响。

为了了解局部图如何分离出每个特征的影响，我们首先考虑单行数据。例如，这一行数据可能代表一支球队有50%的控球率，传球100次，射门10次，进1球。

我们将使用拟合模型来预测我们的结果(他们的球员赢得“全场最佳球员”的概率)。但是我们反复改变一个变量的值来做出一系列的预测。如果球队只有40%的控球率，我们就能预测结果。然后我们预测，他们有50%的几率拿球，然后再预测60%，等等… 我们追踪预测结果(在纵轴上)，当我们从小的控球值移动到大的值(在横轴上)。

在这个描述中，我们只使用了一行数据。特征之间的相互作用可能导致单行的图是非典型的。因此，我们用原始数据集中的多行重复这个心理实验，并在纵轴上绘制平均预测结果。

代码示例

模型构建不是我们的重点，所以我们不会关注数据探索或模型构建代码。

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier

data = pd.read_csv('../input/fifa-2018-match-statistics/FIFA 2018 Statistics.csv')
y = (data['Man of the Match'] == "Yes")  # Convert from string "Yes"/"No" to binary
feature_names = [i for i in data.columns if data[i].dtype in [np.int64]]
X = data[feature_names]
train_X, val_X, train_y, val_y = train_test_split(X, y, random_state=1)
tree_model = DecisionTreeClassifier(random_state=0, max_depth=5, min_samples_split=5).fit(train_X, train_y)
1
2
3
4
5
6
7
8
9
10
11
12

我们的第一个示例使用决策树，如下所示。在实践中，您将在实际应用程序中使用更复杂的模型。

from sklearn import tree
import graphviz

tree_graph = tree.export_graphviz(tree_model, out_file=None, feature_names=feature_names)
graphviz.Source(tree_graph)
1
2
3
4
5

作为阅读树的指导:
有孩子的叶子在顶部显示了它们的分裂标准
底部的一对值分别显示了树的该节点中目标数据点的False值和True值的计数。

下面是使用scikit-learn库创建部分依赖图的代码。

from matplotlib import pyplot as plt
from sklearn.inspection import PartialDependenceDisplay

# Create and plot the data
disp1 = PartialDependenceDisplay.from_estimator(tree_model, val_X, ['Goal Scored'])
plt.show()
1
2
3
4
5
6

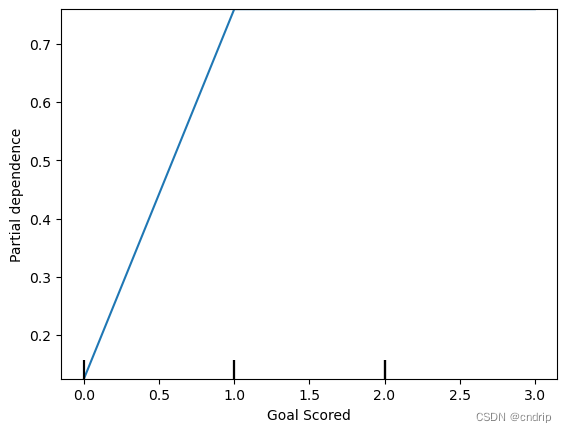
y轴被解释为相对于基线值或最左边值的预测变化。
从这张特殊的图表中，我们可以看到进球大大增加了你赢得“本场最佳球员”的机会。但在此之外的额外目标似乎对预测影响不大。

这里是另一个例子

feature_to_plot = 'Distance Covered (Kms)'
disp2 = PartialDependenceDisplay.from_estimator(tree_model, val_X, [feature_to_plot])
plt.show()
1
2
3

这张图似乎太简单了，不能代表现实情况。但那是因为这个模型太简单了。您应该能够从上面的决策树中看到，它准确地表示了模型的结构。

您可以很容易地比较不同模型的结构或含义。这是随机森林模型的相同图。

# 生成随机森林模型
rf_model = RandomForestClassifier(random_state=0).fit(train_X, train_y)

disp3 = PartialDependenceDisplay.from_estimator(rf_model, val_X, [feature_to_plot])
plt.show()
1
2
3
4
5

这个模型认为，如果你的球员在比赛过程中总共跑了100公里，你就更有可能赢得比赛最佳球员。尽管跑得越多预测越低。

一般来说，这条曲线的平滑形状似乎比决策树模型中的阶跃函数更可信。尽管这个数据集足够小，我们在解释任何模型时都会很小心。

二维部分依赖图

如果您对特征之间的相互作用感到好奇，2D部分依赖图也很有用。举个例子可以说明这一点。

对于这个图，我们将再次使用决策树模型。它将创建一个非常简单的图，但您应该能够将您在图中看到的与树本身相匹配。

fig, ax = plt.subplots(figsize=(8, 6))
f_names = [('Goal Scored', 'Distance Covered (Kms)')]
# Similar to previous PDP plot except we use tuple of features instead of single feature
disp4 = PartialDependenceDisplay.from_estimator(tree_model, val_X, f_names, ax=ax)
plt.show()
1
2
3
4
5

这个图表显示了对进球数和覆盖距离的任何组合的预测。

例如，当一支球队至少进一个球，并且他们的总距离接近100公里时，我们看到的预测最高。如果他们进了0球，距离就不重要了。你能通过0个目标的决策树看到这一点吗?

但如果他们进球，距离会影响预测。确保你能从二维部分依赖图中看到这一点。你能在决策树中看到这种模式吗?

轮到你了

用概念性问题和简短的编码挑战测试你的理解。

---

练习部分

设置

今天，您将创建部分依赖图，并使用来自出租车票价预测竞赛的数据练习构建解释。

我们再次提供了执行基本加载、检查和模型构建的代码。运行下面的单元格设置一切:

import pandas as pd
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split

# Environment Set-Up for feedback system.
from learntools.core import binder
binder.bind(globals())
from learntools.ml_explainability.ex3 import *
print("Setup Complete")

# Data manipulation code below here
data = pd.read_csv('../input/new-york-city-taxi-fare-prediction/train.csv', nrows=50000)

# Remove data with extreme outlier coordinates or negative fares
data = data.query('pickup_latitude > 40.7 and pickup_latitude < 40.8 and ' +
                  'dropoff_latitude > 40.7 and dropoff_latitude < 40.8 and ' +
                  'pickup_longitude > -74 and pickup_longitude < -73.9 and ' +
                  'dropoff_longitude > -74 and dropoff_longitude < -73.9 and ' +
                  'fare_amount > 0'
                  )

y = data.fare_amount

base_features = ['pickup_longitude',
                 'pickup_latitude',
                 'dropoff_longitude',
                 'dropoff_latitude']

X = data[base_features]


train_X, val_X, train_y, val_y = train_test_split(X, y, random_state=1)
first_model = RandomForestRegressor(n_estimators=30, random_state=1).fit(train_X, train_y)
print("Data sample:")
data.head()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

Data sample:

data.describe()
1

问题1

下面是绘制pickup_longitude的部分依赖图的代码。运行以下单元格，不做任何更改。

from matplotlib import pyplot as plt
from sklearn.inspection import PartialDependenceDisplay

feat_name = 'pickup_longitude'
PartialDependenceDisplay.from_estimator(first_model, val_X, [feat_name])
plt.show()
1
2
3
4
5
6

为什么部分依赖图是U形的?
你的解释是否暗示了其他特征的部分依赖图的形状?
在下面的for循环中创建所有其他部分依赖图 (从上面的代码复制适当的行)。

for feat_name in base_features:
    ____
    plt.show()
1
2
3

答案：输入
PartialDependenceDisplay.from_estimator(first_model, val_X, [feat_name])

这些形状是否符合你对它们形状的期望?既然你看到了它们，你能解释一下它们的形状吗?

结论：
从重要性排序结果可以看出，距离是出租车价格最重要的决定因素。

该模型不包括距离度量(如纬度或经度的绝对变化)作为特征，因此坐标特征(如pickup_longitude)获取距离的影响。在经度值的中心附近上车，平均预计票价会降低，因为这意味着更短的行程(以平均计)。

出于同样的原因，我们在所有的部分依赖图中都看到了统一的U形。

问题 2

现在你将运行一个二维部分依赖图。提醒一下，下面是教程中的代码。

fig, ax = plt.subplots(figsize=(8, 6))
f_names = [('Goal Scored', 'Distance Covered (Kms)')]
PartialDependenceDisplay.from_estimator(tree_model, val_X, f_names, ax=ax)
plt.show()
1
2
3
4

为特征pickup_longitude和dropff_longitude创建一个2D图。

你觉得它会是什么样子?

fig, ax = plt.subplots(figsize=(8, 6))

# Add your code here
____
1
2
3
4

答案

f_names = [(‘pickup_longitude’, ‘dropoff_longitude’)]
PartialDependenceDisplay.from_estimator(first_model, val_X, f_names, ax=ax)
plt.show()

结论：
您应该期望该情节具有沿对角线运行的等高线。我们在某种程度上看到了这一点，尽管有一些有趣的警告。

我们期望得到对角线轮廓，因为这些值对在取车和下车经度附近，表明较短的行程(控制其他因素)。

当你离中央对角线越远，我们应该预期价格会随着上下车经度之间的距离增加而增加。

令人惊讶的特征是，当你向图表的右上方走得更远时，价格就会上涨，甚至在45度线附近。

这值得进一步研究，尽管移动到图表右上方的影响与离开45度线相比较小。

创建所需情节所需的代码如下:

fig, ax = plt.subplots(figsize=(8, 6))
fnames = [('pickup_longitude', 'dropoff_longitude')]
disp = PartialDependenceDisplay.from_estimator(first_model, val_X, fnames, ax=ax)
plt.show()
1
2
3
4

问题 3

考虑一下从经度-73.955开始到经度-74结束的旅程。使用上一个问题的图表，估计如果骑手在经度-73.98开始骑行，他们会节省多少钱。

savings_from_shorter_trip = _____ 

# Check your answer
q_3.check()
1
2
3
4

提示：首先找到与-74下降经度对应的垂直水平。然后读取正在切换的水平值。使用等高线来确定自己接近的值的方向。你可以四舍五入到最接近的整数，而不是强调精确的数值。

答案： 6

结论：大约6。

价格从最高的15.16 下降至 8.34 即 15.16-8.34=6. 82 取整为6。

问题 4

到目前为止，在您所看到的 部分依赖图(PDP)中，位置特征主要用作捕捉旅行距离的代理。在置换重要性课程中，您添加了abs_lon_change和abs_lat_change这两个特征，作为距离的更直接度量。
在此处重新创建这些特征。你只需要填写最上面的两行。然后运行以下单元格。
运行它之后，确定这个部分依赖图和没有绝对值特征的图之间最重要的区别。生成没有绝对值特征的PDP的代码位于该代码单元的顶部。

# This is the PDP for pickup_longitude without the absolute difference features. Included here to help compare it to the new PDP you create
feat_name = 'pickup_longitude'
PartialDependenceDisplay.from_estimator(first_model, val_X, [feat_name])
plt.show()

# Your code here
# create new features
data['abs_lon_change'] = ____
data['abs_lat_change'] = ____

features_2  = ['pickup_longitude',
               'pickup_latitude',
               'dropoff_longitude',
               'dropoff_latitude',
               'abs_lat_change',
               'abs_lon_change']

X = data[features_2]
new_train_X, new_val_X, new_train_y, new_val_y = train_test_split(X, y, random_state=1)
second_model = RandomForestRegressor(n_estimators=30, random_state=1).fit(new_train_X, new_train_y)

feat_name = 'pickup_longitude'
disp = PartialDependenceDisplay.from_estimator(second_model, new_val_X, [feat_name])
plt.show()

# Check your answer
q_4.check()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

提示：在创建abs_lat_change和abs_lon_change 特征时使用abs函数。你不需要改变其他任何事情。

答案

# create new features
data[‘abs_lon_change’] = abs(data.dropoff_longitude - data.pickup_longitude)
data[‘abs_lat_change’] = abs(data.dropoff_latitude -
data.pickup_latitude)

结论：
不同的是，部分依赖图变小了。两个图的垂直值最低，均为8.5。但是，顶部图表中的最高垂直值在10.7左右，底部图表中的最大垂直值在9.1以下。换句话说，一旦控制了行驶的绝对距离，pickup_lonitude对预测的影响就会更小。

问题 5

假设您只有两个预测特征，我们称之为feat_a和feat_B。这两个特征的最小值均为-1，最大值均为1。feat_A的部分依赖性图在其整个范围内急剧增加，而feat_B的部分依赖关系图在其全部范围内以较慢的速率（较不陡峭）增加。
这是否保证feat_A将具有比feat_B更高的排列重要性。为什么？
仔细考虑后，取消对下面一行的注释以获得结论。

结论：
不是的。这并不能保证feat_A更重要。例如，feat_A在变化的情况下可能会产生很大的影响，但99%的时间都可能只有一个值。在这种情况下，置换feat_A并不重要，因为大多数值都不会改变。

问题 6

下面的代码单元执行以下操作：

• 1. 创建两个特征X1和X2，其随机值在[-2，2]范围内。
• 2. 创建一个目标变量y，该变量始终为1。
• 3. 在给定X1和X2的情况下训练RandomForestRegressor模型来预测y。
• 4. 创建X1的PDP图和X1与y的散点图。

你对PDP图会是什么样子有预测吗？运行单元格查找结果。
修改y`的初始化，使我们的PDP图在[-1,1]范围内具有正斜率，在其他地方具有负斜率。（注意：您应该只修改y的创建，保持`X1`、`X2`和my_model`不变。）

import numpy as np
from numpy.random import rand

n_samples = 20000

# Create array holding predictive feature
X1 = 4 * rand(n_samples) - 2
X2 = 4 * rand(n_samples) - 2

# Your code here
# Create y. you should have X1 and X2 in the expression for y
y = np.ones(n_samples)

# create dataframe 
my_df = pd.DataFrame({'X1': X1, 'X2': X2, 'y': y})
predictors_df = my_df.drop(['y'], axis=1)

my_model = RandomForestRegressor(n_estimators=30, random_state=1).fit(predictors_df, my_df.y)
disp = PartialDependenceDisplay.from_estimator(my_model, predictors_df, ['X1'])
plt.show()

# Check your answer
q_6.check()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

提示：考虑明确使用包含数学表达式的术语，如（X1<-1）

答案：

将 y = np.ones(n_samples) 修改为
y = -2 * X1 * (X1<-1) + X1 - 2 * X1 * (X1>1) - X2

问题 7

创建一个包含2个特征和一个目标的数据集，使第一个特征的pdp是平坦的，但其排列重要性很高。我们将使用随机森林作为模型。
注意：您只需要提供创建变量X1、X2和y的行。提供了构建模型和计算解释的代码。

import eli5
from eli5.sklearn import PermutationImportance

n_samples = 20000

# Create array holding predictive feature
X1 = ____
X2 = ____
# Create y. you should have X1 and X2 in the expression for y
y = ____


# create dataframe because pdp_isolate expects a dataFrame as an argument
my_df = pd.DataFrame({'X1': X1, 'X2': X2, 'y': y})
predictors_df = my_df.drop(['y'], axis=1)

my_model = RandomForestRegressor(n_estimators=30, random_state=1).fit(predictors_df, my_df.y)


disp = PartialDependenceDisplay.from_estimator(my_model, predictors_df, ['X1'], grid_resolution=300)
plt.show()

perm = PermutationImportance(my_model).fit(predictors_df, my_df.y)

# Check your answer
q_7.check()

# show the weights for the permutation importance you just calculated
eli5.show_weights(perm, feature_names = ['X1', 'X2'])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

提示：X1需要影响预测，才能影响排列的重要性。但是平均效果需要为0才能满足PDP的要求。通过创建交互来实现这一点，因此X1的效果取决于X2的值，反之亦然。

答案

X1 = 4 * rand(n_samples) - 2
X2 = 4 * rand(n_samples) - 2
y = X1 * X2

继续深入

部分依赖图可能非常有趣。我们有一个讨论组，讨论你想看到的部分依赖图解决的现实世界主题或问题。

接下来，了解SHAP 值如何帮助您理解每个预测的逻辑。