​LeetCode解法汇总1465. 切割后面积最大的蛋糕

目录链接：

力扣编程题-解法汇总_分享+记录-CSDN博客

GitHub同步刷题项目：

https://github.com/September26/java-algorithms

原题链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

描述：

矩形蛋糕的高度为 h 且宽度为 w，给你两个整数数组 horizontalCuts 和 verticalCuts，其中：

•  horizontalCuts[i] 是从矩形蛋糕顶部到第  i 个水平切口的距离
• verticalCuts[j] 是从矩形蛋糕的左侧到第 j 个竖直切口的距离

请你按数组 horizontalCuts 和 verticalCuts 中提供的水平和竖直位置切割后，请你找出 面积最大 的那份蛋糕，并返回其 面积 。由于答案可能是一个很大的数字，因此需要将结果 对 109 + 7 取余 后返回。

示例 1：

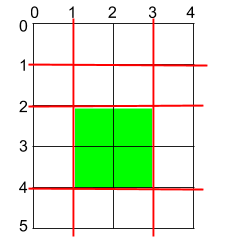
输入：h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3]
输出：4 
解释：上图所示的矩阵蛋糕中，红色线表示水平和竖直方向上的切口。切割蛋糕后，绿色的那份蛋糕面积最大。

示例 2：

输入：h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1]
输出：6
解释：上图所示的矩阵蛋糕中，红色线表示水平和竖直方向上的切口。切割蛋糕后，绿色和黄色的两份蛋糕面积最大。

示例 3：

输入：h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3]
输出：9

提示：

• 2 <= h, w <= 109
• 1 <= horizontalCuts.length <= min(h - 1, 105)
• 1 <= verticalCuts.length <= min(w - 1, 105)
• 1 <= horizontalCuts[i] < h
• 1 <= verticalCuts[i] < w
• 题目数据保证 horizontalCuts 中的所有元素各不相同
• 题目数据保证 verticalCuts 中的所有元素各不相同

解题思路：

把0和h,w分别加入到horizontalCuts和verticalCuts中，然后分别求verticalCuts和verticalCuts中两两之间差值最大的即可。两者相乘就是最大值。

代码：

class Solution {
public:
    int maxArea(int h, int w, vector<int> &horizontalCuts, vector<int> &verticalCuts)
    {
        int maxX = 0;
        int maxY = 0;
        horizontalCuts.push_back(0);
        horizontalCuts.push_back(h);
        verticalCuts.push_back(0);
        verticalCuts.push_back(w);
        sort(horizontalCuts.begin(), horizontalCuts.end());
        sort(verticalCuts.begin(), verticalCuts.end());
        for (int i = 1; i < horizontalCuts.size(); i++)
        {
            maxY = max(maxY, horizontalCuts[i] - horizontalCuts[i - 1]);
        }
 
        for (int i = 1; i < verticalCuts.size(); i++)
        {
            maxX = max(maxX, verticalCuts[i] - verticalCuts[i - 1]);
        }
        int mod = 1e9 + 7;
        return ((long long)maxX * maxY)% mod;
    }
};